【计算理论基础】
1. 语言类的定义
1.1 正则语言
定义:
如果一个语言可以被一台有穷自动机识别,则称它是正则语言。
有穷自动机是一个五元组 ( Q , Σ , δ , q 0 , F ) (Q,Σ,δ,q_0,F) (Q,Σ,δ,q0,F),其中:
- Q Q Q是一个有穷集合,称为状态集。
- Σ Σ Σ是一个有穷集合,称为字母集。
- δ : Q × Σ → Q δ:Q×Σ→Q δ:Q×Σ→Q是转移函数。
- q 0 ∈ Q q_0∈Q q0∈Q是起始状态。
- F ⊆ Q F⊆Q F⊆Q是接受状态集。
举例: L ( M ) = L(M) = L(M)= { w ∣ w w | w w∣w是空串或以0结束}
1.2 上下文无关语言
定义:
与上下文无关文法相关的语言或者被下推自动机PDA识别的语言称为上下文无关语言。
上下文无关文法是一个四元组 ( V , Σ , R , S ) (V,Σ,R,S) (V,Σ,R,S),其中:
- V V V是一个有穷集合,称为变元集。
- Σ Σ Σ是一个与 V V V不相交的有穷集合,称为终结符集。
- R R R是一个有穷规则集,每条规则由一个变元和一个由变元及终结符组成的字符串构成。
- S S S是起始变元。
举例:{ 0 n 1 n ∣ n ≥ 0 0^n1^n | n ≥ 0 0n1n∣n≥0}
1.3 图灵机
定义:
一台图灵机是一个七元组,{ Q , Σ , Q , Σ , Q,Σ, ? , δ , q 0 , q a c c e p t , q r e j e c t δ , q_0 , q_{accept} , q_{reject} δ,q0,qaccept,qreject},其中: Q , Σ , Q , Σ , Q,Σ, ? 都是有限集合,且满足:
- Q Q Q是状态集合。
- Σ Σ Σ是输入字母表,其中不包含特殊的空白符☐。
- ? 是带字母表,其中☐∈? 且Σ ∈? 。
- δ δ δ: Q × Q × Q× ? → Q × → Q × →Q× ? × × × {L,R}是转移函数,其中{L,R}表示读写头是向左移还是向右移。
- q o ∈ Q q_o∈Q qo∈Q是起始状态。
- q a c c e p t q_{accept} qaccept是接受状态。
- q r e j e c t q_{reject} qreject是拒绝状态。 q a c c e p t ≠ q r e j e c t q_{accept} ≠ q_{reject} qaccept=qreject
1.4 图灵可判定语言
定义:
如果一个语言能被某一图灵机判定,则称该语言是图灵可判定的。
举例: A C F G = A_{CFG} = ACFG= { < G , w > ∣ G 是 C F G , w 是 串 , G 派 生 w
1.5 图灵可识别语言
定义:
如果一个语言能被某一图灵机识别,则称该语言是图灵可识别的。
举例: A T M A_{TM} ATM
1.6 非图灵可识别语言
定义:
如果一个语言不能被任何图灵机识别,则称该语言是图灵不可识别的。
举例: ~ A T M ~A_{TM} ~ATM
2. 封闭性证明
2.1 证明正则语言类在并、连接、星号运算下封闭
-
并运算
构造两个有穷自动机 N 1 N 2 N_1N_2 N1N2,分别识别两个正则语言,构造第三个有穷自动机 N N N识别它们俩的并。其中:
N N N的起始状态是新的。
N N N的状态集是它们俩状态集的并再加上 N N N的起始状态。
N N N的接受状态集是它们俩的接受状态集合的并。
只要其中一个有穷自动机接受则接受。 -
连接运算
构造两个有穷自动机 N 1 N 2 N_1N_2 N1N2,分别识别两个正则语言,构造第三个有穷自动机 N N N识别它们俩的连接。其中:
N N N的状态集是 N 1 N 2 N_1N_2 N1N2的状态集的并。
N N N的起始状态是 N 1 N_1 N1的起始状态, N N N的接受状态集是 N 2 N_2 N2的接受状态集。 -
星号
构造一个识别正则语言 A 1 A_1 A1的有穷自动机 N 1 N_1 N1,N是识别A1*的有穷自动机。其中:
N N N的起始状态是新的。
N N N的状态集是 N 1 N_1 N1的状态集 + N N N的起始状态。
N N N的接受状态集是 N 1 N_1 N1的接受状态集 + N N N的起始状态。
2.2 证明图灵可识别语言类在并、连接、星号运算下封闭
- 并运算
构造两个图灵机 M 1 M 2 M_1M_2 M1M2,识别两个图灵可识别语言 A 1 A 2 A_1A_2 A1A2,构造图灵机 M M M,对于输入w:
- 在输入w上并行运行两个图灵机。
- 两个图灵机有一个停机且接受,则接受;若两个都停机且拒绝,则拒绝。
- 则 M M M识别 A 1 ∪ A 2 A_1∪A_2 A1∪A2。
- 连接运算 (每一种分段方式都接受才接受)
构造两个图灵机 M 1 M 2 M_1M_2 M1M2,识别两个图灵可识别语言 A 1 A 2 A_1A_2 A1A2,构造图灵机 M M M,对于输入w:
- 写出所有w的分段方式 ∣ w ∣ + 1 |w| + 1 ∣w∣+1种。
- 对于i = 1,2,重复以下步骤。
- 对于每一种分段方式,在第一段上运行 M 1 M_1 M1i步,在第二段上运行 M 2 M_2 M2i步,或者直到停机。
- 若都接受,则接受。
- 则 M M M为识别 A 1 ∘ A 2 A_1∘A_2 A1∘A2的图灵机。
- 星号(每一种分段方式都接受才接受)
构造一个图灵机 M 1 M_1 M1,识别 A 1 A_1 A1,构造图灵机 M M M,对于输入w:
- 列出所有w的分段方式 2 ( ∣ w ∣ − 1 ) 2^{(|w| - 1)} 2(∣w∣−1)种。
- 对于每一种分段方式,分别在每一段运行 M 1 M_1 M1,直到停机,若都被接受,则接受。
- 否则拒绝。
- 则 M M M是识别 A ∗ A∗ A∗的图灵机。
2.3 证明可判定语言类在并、连接、星号、补、交运算下封闭
- 并运算
构造两个图灵机 M 1 M 2 M_1M_2 M1M2,是识别两个语言 A 1 A 2 A_1A_2 A1A2的判定器,构造图灵机 M M M,对于输入w:
- 在输入w上分别运行 M 1 M 2 M_1M_2 M1M2。
- 两个图灵机有一个接受,则接受;若两个都拒绝,则拒绝。
- 则 M M M为识别 A 1 ∪ A 2 A_1∪A_2 A1∪A2判定器。
- 连接运算 (每一种分段方式都接受才接受)
构造两个图灵机 M 1 M 2 M_1M_2 M1M2,是识别两个语言 A 1 A 2 A_1A_2 A1A2的判定器,构造图灵机 M M M,对于输入w:
- 写出所有w的分段方式。
- 对于i = 1,2,重复以下步骤。
- 对于每一种分段方式,在第一段上运行 M 1 M_1 M1i步,在第二段上运行 M 2 M_2 M2i步,或者直到停机。
- 若都接受,则接受。
- 若有一种不接受,则拒绝。
- 则 M M M为识别 A 1 ∘ A 2 A_1∘A_2 A1∘A2的判定器。
- 星号(每一种分段方式都接受才接受)
构造一个图灵机 M 1 M_1 M1,是识别可判定语言 A 1 A_1 A1的判定器,构造图灵机 M M M,对于输入w:
- 列出所有w的分段方式 2 ( ∣ w ∣ − 1 ) 2^{(|w| - 1)} 2(∣w∣−1)种。
- 对于每一种分段方式,分别在每一段运行 M 1 M_1 M1,直到停机,若都被接受,则接受。
- 否则拒绝。
- 则 M M M是识别A*的判定器。
-
补
设 M 1 M_1 M1 = { Q , Σ , Q , Σ , Q,Σ, ? , δ , q 0 , q 1 , q 2 δ , q_0 , q_1 , q_2 δ,q0,q1,q2}是识别可判定语言A的判定器,则交换接受与拒绝状态的集合得到新的 M M M = { Q , Σ , Q , Σ , Q,Σ, ? , δ , q 0 , q 2 , q 1 δ , q_0 , q_2 , q_1 δ,q0,q2,q1},为识别A的判定器,则可判定语言类在补运算下封闭。 -
交
构造两个图灵机 M 1 M 2 M_1M_2 M1M2,是识别两个语言 A 1 A 2 A_1A_2 A1A2的判定器,构造图灵机M,对于输入w:
- 分别让 M 1 M 2 M_1M_2 M1M2在w上运行。
- 若 M 1 M 2 M_1M_2 M1M2都接受,则接受。
- 否则拒绝。
- M M M是识别 A 1 ∩ A 2 A_1∩A_2 A1∩A2的判定器。
2.4 证明P在并、连接、补运算下封闭
- 并运算
对任意 L 1 , L 2 ∈ P L_1,L_2∈P L1,L2∈P,设有 n a n^a na时间图灵机 M 1 M_1 M1和 n b n^b nb时间图灵机 M 2 M_2 M2判定它们,且 c = m a x ( a , b ) c = max(a,b) c=max(a,b),对 L 1 ∪ L 2 L_1∪L_2 L1∪L2构造判定器 M M M,对于输入w:
- 在输入w上分别运行 M 1 M 2 M_1M_2 M1M2。
- 若有一个接受则接受,否则拒绝。
- 时间复杂度:? ( n a + n b ) = (n^a + n^b) = (na+nb)=? ( n c ) (n^c) (nc),属于P类,因此P类在并运算下封闭。
- 连接运算 (只要有一种分段方式接受就接受)
对任意 L 1 , L 2 ∈ P L_1,L_2∈P L1,L2∈P,设有 n a n^a na时间图灵机 M 1 M_1 M1和 n b n^b nb时间图灵机 M 2 M_2 M2判定它们,且 c = m a x ( a , b ) c = max(a,b) c=max(a,b),对 L 1 ∘ L 2 L_1∘L_2 L1∘L2构造判定器 M M M,对于输入 w = w 1 w 2 . . . . . . w n w = w_1w_2......w_n w=w1w2......wn:
- 对k = 0,1,2,…,n执行下列步骤。
- 在 w 1 w 2 . . . . . . w k w_1w_2......w_k w1w2......wk上运行 M 1 M_1 M1,在 w k + 1 w k + 2 . . . . . . w n w_{k+1}w_{k+2}......w_n wk+1wk+2......wn上运行 M 2 M_2 M2。
- 若都接受,则接受,否则继续。
- 若对任何分法都不接受,则拒绝。
时间复杂度: ( n + 1 ) (n+1) (n+1)(? ( n a ) (n^a) (na) + + + ?( n b ) n^b) nb)) = = = ? ( n a + 1 ) (n^{a + 1}) (na+1) + + + ?( n b + 1 ) = n^{b + 1}) = nb+1)= ? ( n c + 1 ) (n^{c + 1}) (nc+1),属于P类,因此P类在连接运算下封闭。
- 补
对任意 L 1 ∈ P L_1∈P L1∈P,设有 n a n^a na时间图灵机 M 1 M_1 M1判定它,对 ~ L 1 ~L_1 ~L1构造判定器 M M M,对于输入 w w w:
- 在w上运行 M 1 M_1 M1。
- 若 M 1 M_1 M1接受则拒绝,拒绝则接受。
- 时间复杂度:? ( n a ) (n^a) (na),属于P类,因此P类在补运算下封闭。
2.5 证明NP在并、连接、星号运算下封闭
- 并运算
对任意 L 1 , L 2 ∈ P L_1,L_2∈P L1,L2∈P,设有 n a n^a na时间的非确定图灵机 M 1 M_1 M1和 n b n^b nb时间的非确定图灵机 M 2 M_2 M2判定它们,且 c = m a x ( a , b ) c = max(a,b) c=max(a,b),对 L 1 ∪ L 2 L_1∪L_2 L1∪L2构造判定器—非确定图灵机 M M M,对于输入w:
- 在输入w上分别运行 M 1 M 2 M_1M_2 M1M2。
- 若有一个接受则接受,否则拒绝。
- 时间复杂度:? ( n a + n b ) = (n^a + n^b) = (na+nb)=? ( n c ) (n^c) (nc),属于NP类,因此NP类在并运算下封闭。
- 连接运算
对任意 L 1 , L 2 ∈ P L_1,L_2∈P L1,L2∈P,设有 n a n^a na时间的非确定图灵机 M 1 M_1 M1和 n b n^b nb时间的非确定图灵机 M 2 M_2 M2判定它们,且 c = m a x ( a , b ) c = max(a,b) c=max(a,b),对 L 1 ∘ L 2 L_1∘L_2 L1∘L2构造判定器—非确定图灵机 M M M,对于输入 w = w 1 w 2 . . . . . . w n w = w_1w_2......w_n w=w1w2......wn:
- 非确定地把 w w w分成两段 w = x y w = xy w=xy。
- 在 x x x上运行 M 1 M_1 M1,在 y y y上运行 M 2 M_2 M2。
- 若都接受,则接受,否则继续。
时间复杂度:第一步? ( n ) (n) (n),第二步? ( n a + n b ) = (n^a + n^b) = (na+nb)=? ( n c ) (n^c) (nc),属于NP类,因此NP类在连接运算下封闭。
- 星号
设L∈NP,构造非确定图灵机 M M M,对于输入w:
- 非确定地分割 w = w 1 w 2 . . . . . . w k w = w_1w_2......w_k w=w1w2......wk。
- 对于每一段 w i w_i wi,非确定地猜测可证明 w i w_i wi∈L的证书。
- 验证所有可能的证书,则接受。验证失败,则拒绝。
- 在多项式时间内判定L*,则NP在*下封闭。
2.6 证明PSPACE在并、补、星号运算下封闭
3. 可判定/可识别/NP完全证明
3.1 证明 C F L T M CFL_{TM} CFLTM是不可判定的
3.2 证明 E Q T M EQ_{TM} EQTM不是图灵可识别的
3.3 证明 C L I Q U E CLIQUE CLIQUE是NP-完全的
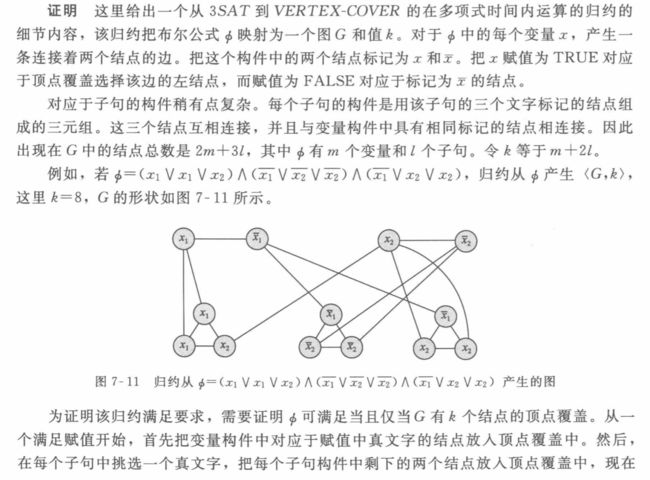
3.4 证明 V E R T E X − C O V E R VERTEX-COVER VERTEX−COVER是NP-完全的

4. 复杂度的包含关系
T I M E ( n 5 ) ⊆ N T I M E ( n 4 ) ⊆ S P A C E ( n 3 ) ⊆ N S P A C E ( n 2 ) ⊆ P S P A C E ⊆ E X P T I M E TIME(n^5)⊆NTIME(n^4)⊆SPACE(n^3)⊆NSPACE(n^2)⊆PSPACE⊆EXPTIME TIME(n5)⊆NTIME(n4)⊆SPACE(n3)⊆NSPACE(n2)⊆PSPACE⊆EXPTIME
- S P A C E ( f ( n ) ) = SPACE(f(n)) = SPACE(f(n))={ L ∣ L L | L L∣L是被? ( f ( n ) ) (f(n)) (f(n))空间的确定性图灵机判定的语言}
- N S P A C E ( f ( n ) ) = NSPACE(f(n)) = NSPACE(f(n))={ L ∣ L L | L L∣L是被? ( f ( n ) ) (f(n)) (f(n))空间的非确定性图灵机判定的语言}
- 萨维奇定理: N S P A C E ( f ( n ) ) ⊆ S P A C E ( f 2 ( n ) ) NSPACE(f(n))⊆SPACE(f^2(n)) NSPACE(f(n))⊆SPACE(f2(n))
- P S P A C E PSPACE PSPACE是在确定性图灵机上,在多项式空间内可以判定的语言类。
- N P S P A C E = P S P A C E NPSPACE = PSPACE NPSPACE=PSPACE
- N P ⊆ P S P A C E NP⊆PSPACE NP⊆PSPACE
- P ⊆ N P ⊆ P S P A C E = N P S P A C E ⊆ E X P T I M E P⊆NP⊆PSPACE = NPSPACE⊆EXPTIME P⊆NP⊆PSPACE=NPSPACE⊆EXPTIME
5. 其他证明
5.1 证明PSPACE难的语言也是NP难的
证明:
若对于任意A ∈ PSPACE,都有A ≤ pB,称B是PSPACE难的。
若对于任意A ∈ NP,都有A ≤ pB,称B是NP难的。
现在B是PSPACE难的,对于任意A ∈ NP,由于NP ⊆ PSPACE,所以A ≤ pB,所以B也是NP难的。
5.2 时间层次定理
保证存在一个语言A,它可以在? ( f ( n ) ) (f(n)) (f(n))时间内判定,但不能在? ( f ( n ) / l o g ( f ( n ) ) ) (f(n)/log(f(n))) (f(n)/log(f(n)))时间内判定。
5.3 空间层次定理
存在语言A,可以在? ( f ( n ) ) (f(n)) (f(n))空间内判定,但不能在? ( f ( n ) ) (f(n)) (f(n))空间内判定。
推论:
S P A C E ( n p ) ⊊ S P A C E ( n q ) , ( p < q ) SPACE(n^p)⊊SPACE(n^q),(p