排序算法总结

本文对各种排序算法进行了原理描述，分析了优缺点及适应场景。基于
《Java数据结构和算法（第二版）》，
作者： Robert Lafore
译者：计晓云 赵研 曾希 狄小菡

目标：把一组棒球队队员按身高排序（从左至右从矮到高）。

简单排序

冒泡排序

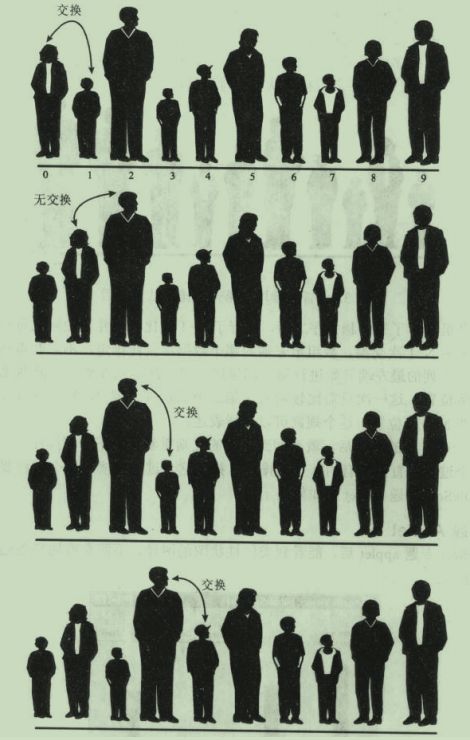
实行方法： 从队列的最左边开始，比较和第一个和第二个队员，如果第一个比较高，则交换他和第二个队员的位置，反之则不作任何动作。然后右移一位，比较站在第二个的队员与站第三个的队员的身高，如果第二个比较高则交换他与第三个队员的位置，反之则不作任何动作，以此类推。过程如下图：

如此完成了第一轮排序，得到下图：

如此最高的人肯定已经到了最右端，这个位置便确定了。再回到最左边依照之前的方法执行第二次排序，确定倒数第二个人的位置，以此类推，直到所有人的位置都确定。
如果一共有N个队员，则此算法要进行N-1轮比较，每一轮比较的次数依次递减。可以看出这个排序算法的名字形象地展示了这一过程，身高最高的人依次香冒泡一样从左边冒到右边。

如此这个算法作比较的次数为：
（N-1）+(N-2)+(N-3)+…+1=N*(N-1)/2,
约等于$N^2/2$算法的运行时间为$O(N^2)$级。

优点：实现逻辑简单，易行。
缺点：运行很慢。

选择排序

从队列最左边开始，记录下第一个人的身高，然后往右挨个比较队员身高与记录值（左边第一人身高），若队员身高小于记录值，更新记录值为此队员身高，直到找到身高最小者，把他与最左的一名队员交换，如此左边第一个位置便固定下来，再从左起第二个位置重复之前的所有操作，下面的图展示了三轮交换的过程：

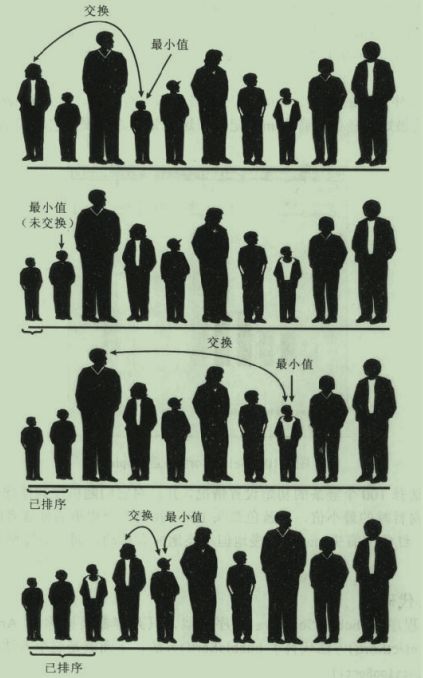
这样一次一次寻找最小者，从左至右依次确定整个队列的顺序。

选择排序相较冒泡排序，把必要的交换次数降为了$O(N)$级，但比较次数仍为$O(N^2)$.

插入排序

应用插入排序的场景常常是“局部有序”的，即某一个队员左边的队员已经按从矮到高的顺序排好了，他右边的队员们是未经排序的，此时我们选取这个队员为“标记队员”， 下面我们想把标记队员插入局部有序的部分的适当位置，首先让“标记队员”出列，然后移动已排序的队员们腾出“标记队员”的位置（把已排序部分从右到左依次与“标记队员”比较，比他高则把该队员右移一位）。流程如下：

完成这一操作后，原“标记队员”右边的队员成为新的“标记队员”，再重复以上操作直至排序完成。

此方法虽然仍然需要$O(N^2)$的时间，但是一般情况下比冒泡排序快一倍，比选择排序还要快一点。经常被用在较复杂的排序算法的最后阶段。

高级排序

希尔排序

此方法基于插入排序，但增加了一个新的特性。插入排序在极端情况下（比如一个最小的数据在最右端）会出现复制次数太多（左边的每个数据都要挨个右移）。希尔排序通过加入插入排序中元素间的间隔，并在这些间隔元素中进行插入从而使数据能够大跨度地移动。如图所示：

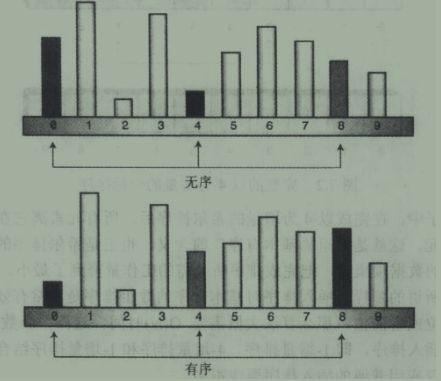
完成对0，4，8号排序后，算法右移一步，排1，5，9号，直到所有的数据都完成了4增量排序。完成一趟排序后，数组可以看成由4个子数组组成：（0，4，8），（1，5，9），（2，6），（3，7），其内部分别是完全有序的，他们交错排列而彼独立，这样，我们说这个数组达成了“基本有序”。希尔排序就是通过达成这种“基本有序”，把完成排序所必需的工作量降到了最小。

完成4-增量排序后，可以减小间隔进行1-增量排序（普通插入排序）。减小间隔也是一门艺术，若是更大的数组，比如1000个数据项，可以先以364为增量，然后减为121，40，13，4，最后用1进行希尔排序，这个用来形成间隔的数列（本例中为364，121，40，13，4，1）被称为间隔序列。这里所表示的序列有Knuth提出。数列以逆向形式从1开始，通过递归表达式
$h=3\ast h+1$
来产生，初始值为1，如下图：

也有其他产生间隔序列的方法，这里只研究Knuth。在排序算法中，h初值赋为1，然后用公式生成序列，当间隔大于数组大小的时候这个过程停止。每完成一次排序，用前面的公式倒推来减小间隔：
$h=(h-1)/3$
当数组用1-增量排序后，算法结束。

这一算法大约需要$O(N\ast (logN{)}^2)$的时间。

优点:，对于多达几千个数据项的中等大小规模数组排序表现良好，非常容易实现，适合在初步尝试的时候使用。在最坏情况和平均情况下效率差别不大。
缺点：对非常大的文件排序不是最优选择（因为慢于复杂度$O(N\ast (logN))$的算法）。

划分

划分是后面快速排序的根本机制，但他本身也是一个有用的操作。划分即把数据分为两组，以一个数值为分界点，大于它的分为一组，小于它的分为一组。此算法由两个指针开始工作，它们分别指向数组的两头。左边的指针逐次右移，右边的指针逐次左移。对于左指针，遇到比枢纽小的数据项时右移，遇到比枢纽大时就停下；对于右指针，遇到比枢纽大的就左移，比枢纽小的就停下；然后左右指针停下时所指的数值交换位置。直至两指针相遇，划分结束。

快速排序

快速排序本质上是通过把一个数组分为两个子数组，然后递归地调用自身为每一个子数组进行快速排序来实现的。但是算法中还需要选择枢纽以及对最小的划分区域进行排序。一般我们选择最右边一个数为枢纽，一次划分完成后直接把他跟右边一组的最左一个数交换位置，则枢纽到了它的最终位置上（左边的数都比它小，右边的数都比它大），不用再动。如图：

在下一次划分中只用对枢纽左右的两个组分别调用自身（划分），直到最后组里只剩一个数值，则划分完成，快速排序过程也完成。

所以快速排序的整体过程是把数组划分为两部分，再把每一部分划分为两部分，如此创建越来越小的子数组，直至划分完成。下图展现了快速排序的过程：

其中不同步骤与递归调用层次的对应关系如下：

这里可以看出对于12个数据项，递归工作栈需要有足够的空间来记录5个参数和返回地址集（每层递归对应一个参数和返回地址集）。所以使用递归算法对规模非常大的数据可能会引起栈溢出，导致错误。

枢纽选择改进:
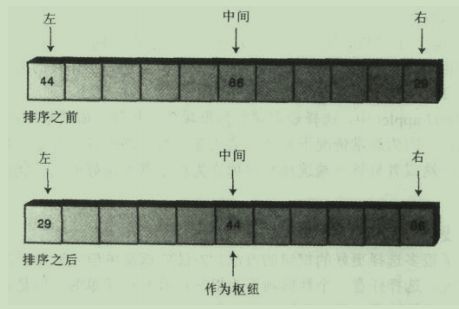
对于之前选择最右端数据作为枢纽的方法，若遇到逆序数据，则算法效率会大大降低。于是为了避免枢纽选到最大或最小值，人们设计出了“三数据项取中”的办法。即找到数组里第一个，中间，和最后一个数，取值居中的数值为枢纽。这样避免了去查找所有数据项中值的费事，同时也避免了选择到极值。如图：

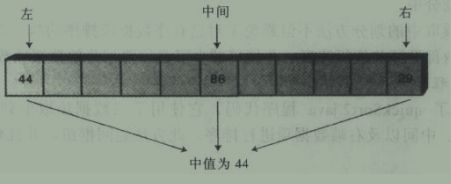
而且在选择枢纽的过程中对这三个数进行了排序，之后就不用再考虑这三个数的位置了（此次调用中，他们都在正确的位置上）。如图：

处理小划分:
三数据项取中划分要求数组不能执行小于等于三个数据项的排序。这是这个“3”被称为切割点。一般我们对切割点个数一下的数组采用插入排序等其他方法。但实际应用中我们一边会把切割点定的稍大一些（在小数组排序中，快速排序优势不明显），如10，20等。
快速排序大约需要$O(N\ast (logN))$的时间。实现的细节问题参考文章一开始的参考书目。

快速排序仍是很常用的排序法。

基数排序

这是一种完全不同的排序法，之前的方法都是通过比较数值来排序，基数排序则是把数值拆为数字位，按数字位的值来排序。特别的是，实现基数排序不需要进行比较。

这里仅列举以10为基数的排序：

1. 根据个位上的值，把所有数据分为10组。
2. 对这10组数据重新排列：把所有0结尾的拍最前面，然后是1，以此类推，此步骤称为第一趟子排序。
3. 在第二趟子排序中，重新把所有数据根据10位上的值分为10组，也是十位上为0的拍最前面，1的排第二…十位为9的组排最后。但是每一组内数据的前后排序遵从第一趟子排序。
4. 再以更高位来排，重复上面过程。直到排完数组中的最高位。

下面展示了一个三位数基数排序的例子来证明此方法的有效性。一共有七个数据：

优缺点： 基数排序只需要执行提取每位上的值与复制操作，对于小型低位数值他的效率可以达到$O(N)$，但是对于大量的数据与高位数数据来说，复制次数与数据项个数和位数的乘积成正比，位数则是数据值的对数，因此绝大多数情况下其执行效率倒退为$O(N\ast (logN))$，与快速排序差不多，但其所需储存空间是快速排序的两倍。