交叉验证和超参数调整:如何优化你的机器学习模型
准确预测Fitbit的睡眠得分
在本文的前两部分中,我获取了Fitbit的睡眠数据并对其进行预处理,将这些数据分为训练集、验证集和测试集,除此之外,我还训练了三种不同的机器学习模型并比较了它们的性能。
在第2部分中,我们看到使用随机森林和xgboost默认超参数,并在验证集上评估模型性能会导致多元线性回归表现最佳,而随机森林和xgboost回归的表现稍差一些。
在本文的这一部分中,我将讨论只使用一个验证集的缺点。除此之外,我们还会谈到如何解决这些缺点以及如何调优模型超参数以提高性能。就让我们一探究竟吧。
交叉验证
简单训练、验证和测试分割的缺点
在本文的第2部分中,我们将数据分为训练、验证和测试集,在训练集上训练我们的模型并在验证集上对模型进行评估。我们还没有接触到测试集,因为它是保留集,它代表的是从未见过的数据,一旦我们觉得机器学习模型有能力进行最终测试,这些数据将用于评估它们的泛化程度。
因为我们只将数据分成了一组训练数据和一组验证数据,所以模型的性能指标高度依赖于这两组数据。机器学习模型只进行一次训练和评估,因此它的性能就取决于那一次评估。而且在对同一数据的不同子集进行训练和评估时,学习模型的表现可能会非常不同,这仅仅是因为选取的子集不同。
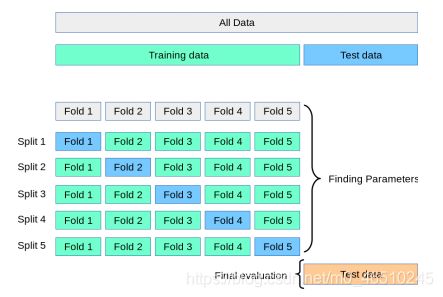
如果我们把这个过程分解为多次训练和验证测试,每次训练和评估我们的模型都是在不同的数据子集上,最后在多次评估中观察模型的平均表现会怎么样呢?这就是K-fold交叉验证背后的想法。
K-fold交叉验证
在K-fold交叉验证(CV)中,我们仍然要先从需要被处理的数据集中分离出一个测试/保留集,以用于模型的最终评估。剩下的数据,即除测试集之外的所有数据,将被分割成K个折叠数(子集)。然后交叉验证迭代这些折叠,在每次迭代中使用一个K折叠作为验证集,同时使用所有剩余的折叠作为训练集。重复这个过程,直到每个折叠都被用作验证集。以下是5倍交叉验证的流程:
将模型在同一个训练数据的不同子集进行K次训练和测试,我们可以更准确地表示我们的模型在它以前没有见过的数据上的表现。在K-fold CV中,我们在每次迭代后对模型进行评分,并计算所有评分的平均值。这样就可以更好地表示该方法与只使用一个训练和验证集相比,模型的表现是怎样的。
Python中的K-fold交叉验证
因为Fitbit睡眠数据集相对较小,所以我将使用4倍交叉验证,并将目前使用的多元线性回归、随机森林和xgboost回归这三种模型进行比较。
请注意,四倍CV可以很好地与第2部分中分离出来的训练数据和验证数据进行比较,因为我们将数据分割为75%的训练数据和25%的验证数据。一个四倍CV本质上也是如此,只是四次,每次使用不同的子集。我创建了一个函数,它将我们想要比较的模型列表,特征数据,目标变量数据以及我们想要创建的折叠数作为输入。该函数计算我们之前使用的性能度量并返回一个表格,其中包含所有模型的平均值以及每种度量类型的每一页的得分,以备我们进一步研究。函数如下:
# Define a function that compares the CV perfromance of a set of predetrmined models
def cv_comparison(models, X, y, cv):
# Initiate a DataFrame for the averages and a list for all measures
cv_accuracies = pd.DataFrame()
maes = []
mses = []
r2s = []
accs = []
# Loop through the models, run a CV, add the average scores to the DataFrame and the scores of
# all CVs to the list
for model in models:
mae = -np.round(cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv), 4)
maes.append(mae)
mae_avg = round(mae.mean(), 4)
mse = -np.round(cross_val_score(model, X, y, scoring='neg_mean_squared_error', cv=cv), 4)
mses.append(mse)
mse_avg = round(mse.mean(), 4)
r2 = np.round(cross_val_score(model, X, y, scoring='r2', cv=cv), 4)
r2s.append(r2)
r2_avg = round(r2.mean(), 4)
acc = np.round((100 - (100 * (mae * len(X))) / sum(y)), 4)
accs.append(acc)
acc_avg = round(acc.mean(), 4)
cv_accuracies[str(model)] = [mae_avg, mse_avg, r2_avg, acc_avg]
cv_accuracies.index = ['Mean Absolute Error', 'Mean Squared Error', 'R^2', 'Accuracy']
return cv_accuracies, maes, mses, r2s, accs
现在我们可以创建一个将要使用的模型列表,并通过4次交叉验证调用上面的函数:
# Create the models to be tested
mlr_reg = LinearRegression()
rf_reg = RandomForestRegressor(random_state=42)
xgb_reg = xgb_regressor = XGBRegressor(random_state=42)
# Put the models in a list to be used for Cross-Validation
models = [mlr_reg, rf_reg, xgb_reg]
# Run the Cross-Validation comparison with the models used in this analysis
comp, maes, mses, r2s, accs = cv_comparison(models, X_train_temp, y_train_temp, 4)
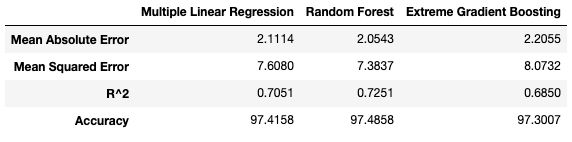
得到的结果对比表如下所示:
使用4倍CV,随机森林回归模型在所有性能指标上都优于其他两个模型。但是在第2部分中,我们看到多元线性回归具有最好的性能指标,为什么会发生变化呢?
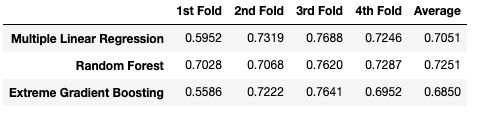
为了理解为什么交叉验证得到的分数与第2部分中简单的训练和验证不同,我们需要仔细看看模型在每个折叠上是如何执行的。上面的cv_compare()函数返回每个折叠中每个不同模型的所有分数的列表。让我们看看三种模型在每次折叠时的r平方是如何比较的。为了得到表格格式的结果,让我们也快速将其转换为数据帧:
# Create DataFrame for all R^2s
r2_comp = pd.DataFrame(r2s, index=comp.columns, columns=['1st Fold', '2nd Fold', '3rd Fold',
'4th Fold'])
# Add a column for the averages
r2_comp['Average'] = np.round(r2_comp.mean(axis=1),4)
上表说明了4倍CV与训练集和验证集得分不同的原因。R-squared在不同的折叠中差异很大,特别是在xgboost和多元线性回归中。这也说明了为什么使用交叉验证如此重要,特别是对于小数据集,如果你只依赖于一个简单的训练集和验证集,你的结果可能会有很大的不同,这个结果就取决于你最终得到的数据分割是什么样子的。
现在我们知道了交叉验证是什么以及它为什么重要,让我们看看是否可以通过调优超参数从我们的模型中获得更多。
超参数调优
模型参数是在模型训练时学习的,不能任意设置。与模型参数不同,超参数是用户在训练机器学习模型前可以设置的参数。随机森林中超参数的例子有:森林中拥有的决策树的数量、每次分割时需要考虑的最大特征数量,或者树的最大深度。
正如我前面提到的,没有一种万能的方法可以找到最优超参数。一组超参数可能在一个机器学习问题上表现良好,但在另一个机器学习问题上可能表现不佳。那么我们怎么得到最优超参数呢?
一种可能的方法是使用有根据的猜测作为起点,手动调整优超参数,更改一些超参数,然后训练模型并评估该模型的性能。一直重复这些步骤,直到我们对性能满意为止。这听起来像是一个不必要的乏味的方法,但的确如此。
比较超参数调整和吉他调弦。你可以选择用你的耳朵来给吉他调音,这种方式需要大量的练习和耐心,而且你可能永远不会得到一个最佳的结果,特别是如果你是一个初学者。但幸运的是,有电子吉他调音器可以帮助你找到正确的音调,它可以解释你吉他弦的声波并显示它所读取的内容。虽然你仍然需要使用机器头来调音琴弦,但过程会快得多,电动调音器会确保你的调音接近最佳状态。那么机器学习和电吉他调音师有什么相同的地方呢?
随机网格搜索交叉验证
优化机器学习超参数最流行的方法之一是scikiti-learn中的RandomizedSearchCV()。让我们仔细分析一下是什么意思。
在随机网格搜索交叉验证中,我们首先创建一个超参数网格,我们想通过尝试优化这些超参数的值,让我们看一个随机森林回归器的超参数网格示例,并看看是如何设置它的:
# Number of trees in Random Forest
rf_n_estimators = [int(x) for x in np.linspace(200, 1000, 5)]
rf_n_estimators.append(1500)
rf_n_estimators.append(2000)
# Maximum number of levels in tree
rf_max_depth = [int(x) for x in np.linspace(5, 55, 11)]
# Add the default as a possible value
rf_max_depth.append(None)
# Number of features to consider at every split
rf_max_features = ['auto', 'sqrt', 'log2']
# Criterion to split on
rf_criterion = ['mse', 'mae']
# Minimum number of samples required to split a node
rf_min_samples_split = [int(x) for x in np.linspace(2, 10, 9)]
# Minimum decrease in impurity required for split to happen
rf_min_impurity_decrease = [0.0, 0.05, 0.1]
# Method of selecting samples for training each tree
rf_bootstrap = [True, False]
# Create the grid
rf_grid = {'n_estimators': rf_n_estimators,
'max_depth': rf_max_depth,
'max_features': rf_max_features,
'criterion': rf_criterion,
'min_samples_split': rf_min_samples_split,
'min_impurity_decrease': rf_min_impurity_decrease,
'bootstrap': rf_bootstrap}
首先,我们为要优化的每个超参数创建一个可能的取值列表,然后使用上面所示的带有键值对的字典来设置网格。为了找到和理解机器学习模型的超参数,你可以查阅模型的官方文档。
生成的网格如下所示:
顾名思义,随机网格搜索交叉验证使用交叉验证来评估模型性能。随机搜索意味着算法不是尝试所有可能的超参数组合(在我们的例子中是27216个组合),而是随机从网格中为每个超参数选择一个值,并使用这些超参数的随机组合来评估模型。
用计算机将所有可能的组合都尝试一遍是非常昂贵的,而且需要很长时间。随机选择超参数可以显著地加快这个过程,并且通常为尝试所有可能的组合提供了一个类似的好的解决方案。让我们看看随机网格搜索交叉验证是如何使用的。
随机森林的超参数整定
使用先前创建的网格,我们可以为我们的随机森林回归器找到最佳的超参数。因为数据集相对较小,我将使用3倍的CV并运行200个随机组合。因此,随机网格搜索CV总共将要训练和评估600个模型(200个组合的3倍)。由于与其他机器学习模型(如xgboost)相比,随机森林的计算速度较慢,运行这些模型需要几分钟时间。一旦这个过程完成,我们就可以得到最佳的超参数。
以下展示了如何使用RandomizedSearchCV():
# Create the model to be tuned
rf_base = RandomForestRegressor()
# Create the random search Random Forest
rf_random = RandomizedSearchCV(estimator = rf_base, param_distributions = rf_grid,
n_iter = 200, cv = 3, verbose = 2, random_state = 42,
n_jobs = -1)
# Fit the random search model
rf_random.fit(X_train_temp, y_train_temp)
# View the best parameters from the random search
rf_random.best_params_
我们将在最终模型中使用这些超参数,并在测试集上对模型进行测试。
xgboost的超参数整定
对于我们的xgboost回归,过程基本上与随机森林相同。由于模型的性质,我们试图优化的超参数有一些是相同的,有一些是不同的。您可以在这里找到xgb回归器超参数的完整列表和解释。我们再次创建网格:
# Number of trees to be used
xgb_n_estimators = [int(x) for x in np.linspace(200, 2000, 10)]
# Maximum number of levels in tree
xgb_max_depth = [int(x) for x in np.linspace(2, 20, 10)]
# Minimum number of instaces needed in each node
xgb_min_child_weight = [int(x) for x in np.linspace(1, 10, 10)]
# Tree construction algorithm used in XGBoost
xgb_tree_method = ['auto', 'exact', 'approx', 'hist', 'gpu_hist']
# Learning rate
xgb_eta = [x for x in np.linspace(0.1, 0.6, 6)]
# Minimum loss reduction required to make further partition
xgb_gamma = [int(x) for x in np.linspace(0, 0.5, 6)]
# Learning objective used
xgb_objective = ['reg:squarederror', 'reg:squaredlogerror']
# Create the grid
xgb_grid = {'n_estimators': xgb_n_estimators,
'max_depth': xgb_max_depth,
'min_child_weight': xgb_min_child_weight,
'tree_method': xgb_tree_method,
'eta': xgb_eta,
'gamma': xgb_gamma,
'objective': xgb_objective}
生成的网格如下所示:
为了使性能评估具有可比性,我还将使用具有200个组合的3倍CV来进行xgboost:
# Create the model to be tuned
xgb_base = XGBRegressor()
# Create the random search Random Forest
xgb_random = RandomizedSearchCV(estimator = xgb_base, param_distributions = xgb_grid,
n_iter = 200, cv = 3, verbose = 2,
random_state = 420, n_jobs = -1)
# Fit the random search model
xgb_random.fit(X_train_temp, y_train_temp)
# Get the optimal parameters
xgb_random.best_params_
最优超参数如下:
同样的,这些将在最终的模型中使用。
虽然对有些人来说这可能是显而易见的,但我只是想在这里提一下:我们为什么不为多元线性回归做超参数优化是因为模型中没有超参数需要调整,它只是一个多元线性回归。
现在我们已经获得了最佳的超参数(至少在交叉验证方面),我们终于可以在测试数据上评估我们的模型了,我们就可以根据我们从一开始就持有的测试数据来评估我们的模型了!
最终模型的评估
在评估了我们的机器学习模型的性能并找到了最佳超参数之后,是时候对模型进行最后的测试了。
我们对模型进行了训练,这些数据是我们用于进行评估的数据的80%,即除了测试集之外的所有数据。我们使用上一部分中找到的超参数,然后比较模型在测试集上的表现。
让我们创建和训练我们的模型:
# Create the final Multiple Linear Regression
mlr_final = LinearRegression()
# Create the final Random Forest
rf_final = RandomForestRegressor(n_estimators = 200,
min_samples_split = 6,
min_impurity_decrease = 0.0,
max_features = 'sqrt',
max_depth = 25,
criterion = 'mae',
bootstrap = True,
random_state = 42)
# Create the fnal Extreme Gradient Booster
xgb_final = XGBRegressor(tree_method = 'exact',
objective = 'reg:squarederror',
n_estimators = 1600,
min_child_weight = 6,
max_depth = 8,
gamma = 0,
eta = 0.1,
random_state = 42)
# Train the models using 80% of the original data
mlr_final.fit(X_train_temp, y_train_temp)
rf_final.fit(X_train_temp, y_train_temp)
xgb_final.fit(X_train_temp, y_train_temp)
我定义了一个函数,该函数对所有最终模型进行评分,并创建了一个更容易比较的数据帧:
# Define a function that compares all final models
def final_comparison(models, test_features, test_labels):
scores = pd.DataFrame()
for model in models:
predictions = model.predict(test_features)
mae = round(mean_absolute_error(test_labels, predictions), 4)
mse = round(mean_squared_error(test_labels, predictions), 4)
r2 = round(r2_score(test_labels, predictions), 4)
errors = abs(predictions - test_labels)
mape = 100 * np.mean(errors / test_labels)
accuracy = round(100 - mape, 4)
scores[str(model)] = [mae, mse, r2, accuracy]
scores.index = ['Mean Absolute Error', 'Mean Squared Error', 'R^2', 'Accuracy']
return scores
使用我们的三个最终模型调用该函数并调整列标题将会得到以下最终计算结果:
# Call the comparison function with the three final models
final_scores = final_comparison([mlr_final, rf_final, xgb_final], X_test, y_test)
# Adjust the column headers
final_scores.columns = ['Linear Regression', 'Random Forest', 'Extreme Gradient Boosting']
获胜者是:随机森林回归!
随机森林的R-squared达到80%,测试集的准确率为97.6%,这意味着它的预测平均只有2.4%的偏差。这是个不错的结果!
在此分析中,多元线性回归的表现并不逊色,但xgboost并没有达到其所宣传的效果。
总结评论
整个分析过程和实际操作过程都很有趣。我一直在研究Fitbit是如何计算睡眠分数的,现在我很高兴能更好地理解它。最重要的是,我建立了一个机器学习模型,可以非常准确地预测睡眠分数。话虽如此,我还是想强调几件事:
- 正如我在第2部分中提到的,对多元线性回归系数的解释可能不准确,因为特征之间存在高度的多重共线性。
- 我用于分析的数据集相当小,因为它依赖于从Fitbit获得的286个数据点。这限制了结果的可推广性,需要更大的数据集才能训练出更健壮的模型。
- 该分析仅使用了Fitbit的一个人的睡眠数据,因此可能不能很好地推广到其他睡眠模式、心率等不同的人。
我希望你喜欢这篇关于如何使用机器学习来预测Fitbit睡眠分数的全面分析,并且了解了不同睡眠阶段的重要性以及睡眠过程中所花费的时间。
感谢你的阅读!
作者:Jonas Benner
deephub翻译组:钱三一