逻辑回归和多类逻辑回归
逻辑回归概念
逻辑回归是一个非常经典,也是很常用的模型。看到逻辑回归这个名字,你以为这是一个“回归模型”,但是其实它是一个分类模型,是使用线性区分模型泛化感知器。
在逻辑回归中就是基于sigmoid函数构建的模型。sigmoid函数的数学定义如下:
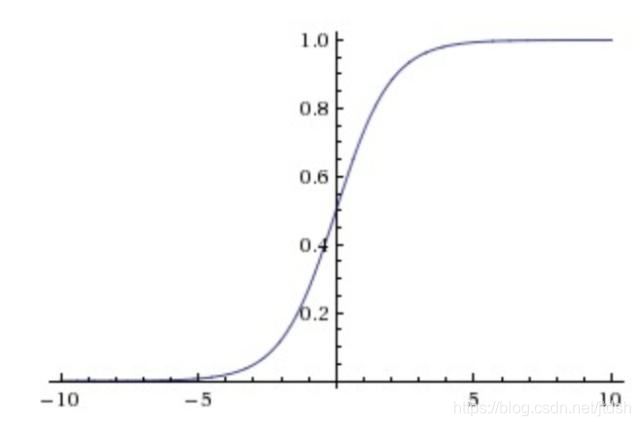
σ ( x ) = 1 1 + e − x \sigma(x)=\cfrac{1}{1 +e^{-x}} σ(x)=1+e−x1
图中我们可以直观地看到这个函数的一些特点:
- 中间范围内函数斜率最大,对应Y的大部分数值变化
- Y轴数值范围在 0~1 之间
- X轴数值范围没有限制,但当X大于一定数值后,Y无限趋近于1,而小于一定数值后,Y无限趋近于0
- 特别地,当 X=0 时,Y=0.5
我们假设:
(1)假设数据服从伯努利分布
(2)假设模型的输出值是样本为正例的概率
sigmoid函数可以将任意的实数映射为0到1之间的某个值。因此,逻辑回归的输出可以作为任何一个分类的后验概率。其对应的公式可以表示如下:
p ( C = 1 ∣ x ) = y ( x ) = σ ( w T x + b ) p(C=1| \ x)=y(x)=\sigma(w^Tx+b) p(C=1∣ x)=y(x)=σ(wTx+b)
p ( C = 0 ∣ x ) = 1 − p ( C = 1 ∣ x ) p(C=0|x)=1-p(C=1|\ x) p(C=0∣x)=1−p(C=1∣ x)
这两公式可以整合在一起,如下(没有什么特殊含义,就是归纳成一个式子): p ( C = t ∣ x ) = y t ( 1 − y ) 1 − t p(C=t|\ x)=y^t(1-y)^{1-t} p(C=t∣ x)=yt(1−y)1−t
这里 t ∈ { 0 , 1 } t\in \{0,1\} t∈{0,1}.
对于这个函数:
P ( x ∣ θ ) P(x|θ) P(x∣θ)
输入有两个: x x x 表示某一个具体的数据; θ \theta θ表示模型的参数。
如果 θ \theta θ是已知确定的, x x x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点 x x x,其出现概率是多少。
如果 x x x是已知确定的, θ \theta θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现 x x x这个样本点的概率是多少。
y ( x ) y(x) y(x)的输入是一个样本,输出是这个样本属于各个类的概率。假设这个样本属于1类,那我是不是希望模型 y ( x ) y(x) y(x)输出的概率中认为样本属于1类的概率越大越好?换句话说就是,w,b各种可能的取值对应各种假设的模型。能让模型认为样本属于1类的概率最大的那种情况的参数是最好的,这就是极大似然法的动机。
我们选择了w,b的一种可能的取值然后确定了一个模型 y ( x ) y(x) y(x)。现在有N个样本,输入到模型 y ( x ) y(x) y(x)。那么会有N个值,这N个值表明了这些样本属于样本A的概率。他们同时发生的概率就是这些概率相乘。
这些样本都是自己有标签的。我们希望模型输出来他们属于它标签的那个类的概率尽可能的大。这个想法就是极大似然法的想法。那么现在问题来了,模型计算他们属于它标签的那个概率?
答:模型输出都是样本属于A的概率。逻辑回归只能分出两种类,要么是A要么不是A。现在我们知道了样本属于A的概率,那么样本属于B的概率=样本不属于A的概率。
举个例子:y(样本1)=0.2,然后样本1的标签是A,那么模型计算出来样本属于B的概率是1−f(样本1)=1−0.2。
基于前面的公式,用于评估模型参数的最大似然值的似然函数可以用下面的公式表示: L ( w , b ) = ∏ n = 1 N y n t n ( 1 − y n ) 1 − t n L(w,b)=\prod_{n=1}^N{y_n^{t_n}(1-y_n)^{1-t_n}} L(w,b)=n=1∏Nyntn(1−yn)1−tn
其中, y n = p ( C = 1 ∣ x n ) y_n=p(C=1|x_n) yn=p(C=1∣xn)
我们要做的是不断改动w,b,找到一个让上面那个式子最大的w,b。这就是极大似然做的事。根据概率找最优的参数。不过这种计算量让人担忧,因为函数存在乘法计算。为了简化计算,我们对似然函数取对数。除此之外,我们对符号进行了替换,目的是最小化似然函数的负对数结果。由于对数函数单调递增的,所以原函数的关系不会发生变化。公式如下: E ( w , b ) = − ln L ( w , b ) = − ∑ n = 1 N { t n ln y n + ( 1 − t n ) ln ( 1 − y n ) } E(w,b)=-\ln{L(w,b)}=-\sum_{n=1}^N{\{t_n\ln y_n+(1-t_n)\ln (1-y_n)\}} E(w,b)=−lnL(w,b)=−n=1∑N{tnlnyn+(1−tn)ln(1−yn)}
其中包括误差函数,这种类型的函数称之为交叉熵误差函数。
与感知器类似(可参考之前的博客),可通过计算模型参数w和b的梯度,对模型进行优化。公式如下:
∂ E ( w , b ) ∂ w = − ∑ n = 1 N ( t n − y n ) x n \cfrac{\partial E(w,b) }{\partial w}=-\sum_{n=1}^N{(t_n-y_n)x_n} ∂w∂E(w,b)=−n=1∑N(tn−yn)xn
∂ E ( w , b ) ∂ b = − ∑ n = 1 N ( t n − y n ) \cfrac{\partial E(w,b) }{\partial b}=-\sum_{n=1}^N{(t_n-y_n)} ∂b∂E(w,b)=−n=1∑N(tn−yn)
根据这些公式,我们可以更新模型参数,如下所示:
w ( k + 1 ) = w k − η ∂ E ( w , b ) ∂ w = w k + η ∑ n = 1 N ( t n − y n ) x n w^{(k+1)}=w^{k}-\eta \cfrac{\partial E(w,b) }{\partial w}=w^{k}+ \eta \sum_{n=1}^N{(t_n-y_n)x_n} w(k+1)=wk−η∂w∂E(w,b)=wk+ηn=1∑N(tn−yn)xn
b ( k + 1 ) = b k − η ∂ E ( w , b ) ∂ b = b k + η ∑ n = 1 N ( t n − y n ) b^{(k+1)}=b^{k}-\eta \cfrac{\partial E(w,b) }{\partial b}=b^{k}+ \eta \sum_{n=1}^N{(t_n-y_n)} b(k+1)=bk−η∂b∂E(w,b)=bk+ηn=1∑N(tn−yn)
因为要计算所有数据的总和,才能得出每次迭代的梯度。一旦数据集变大,计算的开销将会增大。所以,通常采用另一种方式来进行,即从数据集中选择部分的数据,仅对这些选中的数据求和来计算梯度,从而更新模型的参数。这种方法称为“随机梯度下降法”,简称SGD。
多类逻辑回归概念
我们已经知道,普通的逻辑回归只能针对二分类(Binary Classification)问题,要想实现多个类别的分类,我们必须要改进逻辑回归,让其适应多分类问题。
在二分类中,激活函数是sigmoid函数,因为输出值介于0和1之间,所以你可以根据输出值对数据进行分类。
在K分类中,激活函数是softmax函数,而softmax函数是sigmoid函数的多变量版本,函数定义如下: p ( C = k ∣ x ) = y k ( x ) = exp ( w k T x + b k ) ∑ j = 1 K exp ( w j T x + b j ) p(C=k|\ x)=y_k(x)=\cfrac{\exp(w_k^Tx+b_k)}{\sum_{j=1}^K{\exp(w_j^Tx+b_j)}} p(C=k∣ x)=yk(x)=∑j=1Kexp(wjTx+bj)exp(wkTx+bk)
通过这个图片可以更直观展示(图片来自网络):

补充:实际应用中,使用 Softmax 需要注意数值溢出的问题。因为有指数运算,如果 Z数值很大,经过指数运算后的数值往往可能有溢出的可能。所以,需要对 Z 进行一些数值处理:即 Z 中的每个元素减去 V 中的最大值。
如下:
public static double[] softmax(double[] x, int n) {
double[] y = new double[n];
double max = 0.;
double sum = 0.;
for (int i = 0; i < n; i++) {
if (max < x[i]) {
max = x[i]; // 防止溢出
}
}
for (int i = 0; i < n; i++) {
y[i] = Math.exp( x[i] - max );
sum += y[i];
}
for (int i = 0; i < n; i++) {
y[i] /= sum;
}
return y;
}
得到的似然函数对应如下:
L ( w , b ) = ∏ n = 1 N ∏ k = 1 K y n k t n k L(w,b)=\prod_{n=1}^N{\prod_{k=1}^K{y_{nk}^{t_{nk}}}} L(w,b)=n=1∏Nk=1∏Kynktnk
E ( w , b ) = − ln L ( w , b ) = − ∑ n = 1 N ∑ k = 1 K t n k ln y n k E(w,b)=-\ln L(w,b)=-\sum_{n=1}^N{\sum_{k=1}^K{t_{nk}\ln y_{nk}}} E(w,b)=−lnL(w,b)=−n=1∑Nk=1∑Ktnklnynk
梯度对应为:
∂ E ( w , b ) ∂ w j = − ∑ n = 1 N ( t n j − y n j ) x n \cfrac{\partial E(w,b) }{\partial w_j}=-\sum_{n=1}^N{(t_{nj}-y_{nj})x_n} ∂wj∂E(w,b)=−n=1∑N(tnj−ynj)xn
∂ E ( w , b ) ∂ b j = − ∑ n = 1 N ( t n j − y n j ) \cfrac{\partial E(w,b) }{\partial b_j}=-\sum_{n=1}^N{(t_{nj}-y_{nj})} ∂bj∂E(w,b)=−n=1∑N(tnj−ynj)