深度学习(七)-卷积神经网络实现 MNIST 手写数字分类

  在深度学习(五)-全连接神经网络实现 $MNIST$ 手写数字分类中，我是用全连接神经网络实现了 $MINST$ 手写数字分类，这里我就不再介绍 $MINST$ 数据集和数据的处理了，我们直接进入主题，创建卷积神经网络。

网络模型创建

  我们可以先创建一个最简单的三层神经网络，两层卷积层，两层池化层，一层全连接层：

	class simpleCNN(nn.Module):
	    def __init__(self):
	        super(simpleCNN, self).__init__()
	        self.layer1 = nn.Sequential(  # 1, 28, 28
	            nn.Conv2d(1, 16, 5, 1, 2),   # 卷积层,输入深度为1,输出深度16,卷积核5*5,步长1,padding=(kernel_size-1)/2如果stride=1
	            nn.ReLU(),  # 激活层
	            nn.MaxPool2d(kernel_size=2)  # 池化层
	        )  # 输出: 16, 14, 14
	        
	        self.layer2 = nn.Sequential(   # 全连接层 
	            nn.Linear(16*14*14, 10)   # 32*7*7
	        )
	        
	    def forward(self, x):
	        x = self.layer1(x)
	        x = x.view(x.size(0), -1)   # 多维展开
	        output = self.layer2(x)
	        
	        return output

  在全连接神经网络 MINST 手写数字分类中，我们看到一张图片的大小为 $[1,28,28]$，即 深度为 $1$，高度 $28$， 宽度 $28$。$nn.Conv2d(1,16,5,1,2)$ 函数中，我们定义输出深度定义为 $16$，卷积核大小定义为 $5$X$5$，滑动步长定义为 $1$，使输出空间与输入空间相同尺寸，那么可以通过输出空间公式 $(n-m+2p)/s+1$，得到填充 $0$ 的数量为 $2$。
  卷积层的输出为 $[16，28，28]$，经过激活层 $nn.ReLU()$，使用 2X2 的 两层池化层池化，得到池化层输出空间大小为 $[16,14,14]$。那么全连接层的输入空间大小就为 $16$X$14$X$14$。
  网络创建好之后，我们可以加载网络，看看网络层的参数

	model = simpleCNN()
	
	model.parameters

模型训练

  模型训练包括优化函数和损失函数都和全连接层实现的是一样，优化函数的学习率设置为 $1e-3$，不同的学习率会导致训练效果不同，自己根据实际情况调整。 这里我就不贴代码出来了，还不会的童鞋可以参考深度学习(五)-全连接神经网络实现 $MNIST$ 手写数字分类，我这里同样是将数据集训练 $20$ 次，直接给大家看看训练的效果：

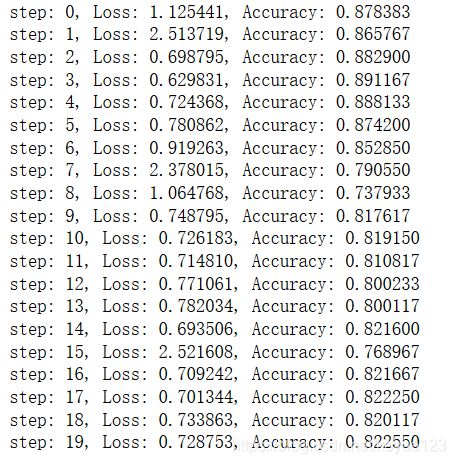
  结果发现准确率只有 $82.25\%$，而且还不稳定。同样将测试集带入测试，看看效果：

  测试正确率同样只有 $81.9\%$，效果同样不理想，造成这个原因是因为我们的模型深度太浅，下面我们重新优化一下，忘了哪位大神说的，只要你觉得神经网络的模型效果差，那就多加几层，深度越深，效果一般都会越来越好，我们就来试试。

模型优化

  因为电脑配置的原因，我这里只是用了 $9$ 层网络，每层的输入和输出我都有注释，不懂的小伙伴可以参考上面。

	class CNN(nn.Module):
	    def __init__(self):
	        super(CNN, self).__init__()
	        self.layer1 = nn.Sequential(    		# [1, 28, 28]
	            nn.Conv2d(1, 16, kernel_size=3),  	# [16, 26, 26]
	            nn.BatchNorm2d(16),
	            nn.ReLU()
	        )
	        
	        self.layer2 = nn.Sequential( 			 # [16, 26, 26]
	            nn.Conv2d(16, 32, kernel_size=3),  	 # [32, 24, 24]
	            nn.BatchNorm2d(32),
	            nn.ReLU(),
	            nn.MaxPool2d(kernel_size=2, stride=2)	# [32, 12, 12]
	        )
	        
	        self.layer3 = nn.Sequential(     		# [32, 12, 12]
	            nn.Conv2d(32, 64, kernel_size=3),   # [64, 10, 10]
	            nn.BatchNorm2d(64),
	            nn.ReLU()
	        )
	        
	        self.layer4 = nn.Sequential(  			# [64, 10, 10]
	            nn.Conv2d(64, 128, kernel_size=3),  # [128, 8, 8]
	            nn.BatchNorm2d(128),
	            nn.ReLU(),
	            nn.MaxPool2d(kernel_size=2, stride=2) 	# [128, 4, 4]
	        )
	        
	        self.fc = nn.Sequential(
	            nn.Linear(128*4*4, 1024),
	            nn.ReLU(),
	            nn.Linear(1024, 128),
	            nn.ReLU(),
	            nn.Linear(128, 10),
	        )
	        
	    def forward(self, x):
	        x = self.layer1(x)
	        x = self.layer2(x)
	        x = self.layer3(x)
	        x = self.layer4(x)
	        x = x.view(x.size(0), -1) 
	        output = self.fc(x)
	        
	        return output

  我们同样看看网络层的参数：

	model = CNN()
	model.parameters

  使用同样的优化函数，设置学习率为 $1e-3$，同样训练 $20$ 次，来看看效果有没有好点：

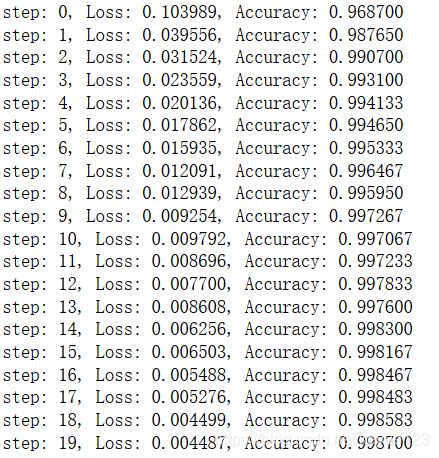
  可以发现，准确率可以达到的 $99.87\%$，比之前明显提升很多，我们带入测试集测试一下：

	eval_loss = 0
	eval_acc = 0
	model.eval() # 将模型改为预测模式
	for step, (image, label) in enumerate(test_data):
	    image = Variable(image)
	    label = Variable(label)
	        
	    out = model(image)
	    
	    loss = criterion(out, label)
	    # 记录误差
	    eval_loss += loss.data
	    # 记录准确率
	    _, pred = out.max(1)
	    num_correct = (pred == label).sum().item()
	    acc = num_correct / image.shape[0]
	    eval_acc += acc
	
	print('Test Loss: {:.6f}, Test Accuracy: {:.6f}'.format(eval_loss/len(test_data), eval_acc/len(test_data)))

  测试准确率也有 $99.5\%$，效果明显不过，大家可以动手试试。