keras快速搭建神经网络进行电影文本评论二分类
在本次博客中,将讨论英语文本分类问题,可同样适用于文本情感分类,属性分类等文本二分类问题。
1、数据准备
使用 IMDB 数据集,它包含来自互联网电影数据库(IMDB)的 50 000 条严重两极分化的评论。数据集被分为用于训练的 25 000 条评论与用于测试的 25 000 条评论,训练集和测试集都包含 50% 的正面评论和 50% 的负面评论。
这个数据集已经在keras的database里面有下载和读取的方法,这里我们直接调用即可。
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
我们来打印出数据的一些信息
# 打印数据集大小及部分数据信息
print(train_data.shape)
print(train_data[0])
print(train_labels)
print(test_labels.shape)
可以看出,训练集和测试集都有25000条评论,每条评论是一个长度不等的向量。在这个数据集中,每条评论已经编码为数字,具体编码流程如下:
首先,对25000条评论分词,词形还原,再进行词频统计,按照出现频率从高到低编号1,2,3…接下来,把每一条评论里面各个单词转化为对应标号,即组成这里的每条评论行向量。
举个例子,假设词频统计结果为{“I”: 29, “love”: 49, “you”: 21, “don’t”: 34, “hurt”: 102},那么一条评论为"I hurt you"的行向量即为[29, 102, 21]
在这个数据集里面,keras也提供了每个单词编号对应编号这样一个字典,这就意味着我们可以反解析出每条评论。
word_index = imdb.get_word_index() # word_index是一个字典,键为单词,值为编码后的数字
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()]) # 将键值交换
这样,reverse_word_index就记录了每个编号对应的单词,我们就可以反解析每条评论啦~
'''
还原第一条评论信息.注意,索引减去了 3,因为 0、1、2是为“padding”(填充)、
“start of sequence”(序列开始)、“unknown”(未知词)分别保留的索引
'''
decoded_review = ' '.join([reverse_word_index.get(i-3, '?') for i in train_data[0]])
我们打印出第一条评论的文字信息:
? this film was just brilliant casting location scenery story direction
everyone's really suited the part they played and you could just imagine being there robert ?
is an amazing actor and now the same being director ? father came from the same scottish island as myself
so i loved the fact there was a real connection with this film the witty remarks throughout
the film were great it was just brilliant so much that i bought the film as soon as it was released for ?
and would recommend it to everyone to watch and the fly fishing was amazing really cried at the end it was so sad and you know what they say if you cry at a film
it must have been good and this definitely was also ?
to the two little boy's that played the ? of norman and paul they were just brilliant children are often left out of the ? list
i think because the stars that play them all grown up are such a big profile for the whole film
but these children are amazing and should be praised for what they have done
don't you think the whole story was so lovely because it was true and was someone's life after all that was shared with us all
2、数据预处理:对数据简单编码
因为一共10000个单词(我们只选取了10000个出现频率最高的单词),我们给每条评论的向量初始化为10000个0的行向量,依次看每条评论出现单词的编号是多少,在对应编号处将其置为1。假设某条评论出现单词编号以此为12,250, 3600,则该评论处理后的向量为10000个零, 将第12, 250, 3600个零置为1。
# 使用one-hot编码,使列表转化为大小一致的张量
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension)) # 创建一个sequences行,10000列的0向量
for i, sequence in enumerate(sequences):
results[i, sequence] = 1 # 将单词出现指定处置为1
return results
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
与此同时,我们也将标签向量化:
import numpy as np
# 将标签向量化
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
3、建立模型
在keras里面,模型可以通过models.Sequential()或者API建立。这里我们用最常用的models.Sequential()
# 建立模型
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
接下来对神经网络层数,每层神经元个数,激活函数等加以说明。这里我们设置了三层神经网络,两个隐藏层, 一个输出层。考虑到数据量较小,这里只有两个隐藏层,且隐藏层神经元个数也较少(16和16,一般设置为2的幂)。因为这是二分类问题,所有最后一层,即输出层只有一个神经元,且用“sigmod”输出为二分类的概率。注意sigmod一般用于二分类问题,多分类问题输出概率时用"softmax"。激活函数在隐藏层都是"relu",也可以是"tanh"等,但不能是"sigmod",想一想这是为什么???“sigmod"这个函数求导后最大值在0处取得,为0.25,远小于1,当数据流入每一层神经网络时都会进行链式求导,自然就会让输入数据越来越小,导致"梯度弥散”,导致“早停”,达不到训练效果。
4、模型训练
model.compile(
optimizer=RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['accuracy'])
优化器选择随机梯度下降(SGD)的变体,RMSprop,学习率为0.001,损失函数为二分类的交叉熵,评估指标为准确率。
因为这个数据集训练集和测试集完全一样,导致我们只能用一个。所有我们将训练集里面划分一下,后15000条评论作为训练模型用,前10000条评论作为测试用。
train_partion_data = x_train[10000:]
train_partion_label = y_train[10000:]
test_partion_data = x_train[:10000]
test_partion_label = y_train[:10000]
接下来开始训练:
history = model.fit(
train_partion_data,
train_partion_label,
epochs=20, batch_size=512,
validation_data=(test_partion_data, test_partion_label))
用fit函数进行训练,前两个参数是训练集数据和标签,epochs是训练多少轮,batch_size是一次训练传入多少样本,validation_data里面是测试数据和标签,每一轮训练完后都会用这里面数据测试一下准确率。
最后别忘了保存训练好的模型,以便进行后期继续训练后者直接用于实际预测、分析和可视化。
print(history.history)
model.save('IMDB.json')
模型训练后有个history方法,里面记录了每一轮训练的损失值和准确率,方便可视化和观察在第几轮开始出现过拟合。
5、结果展示、可视化和分析
首先看看第一轮训练结果和最后一轮训练结果:
Epoch 1/20
512/15000 [>.............................] - ETA: 2:10 - loss: 0.6931 - acc: 0.5020
1024/15000 [=>............................] - ETA: 1:03 - loss: 0.6841 - acc: 0.5850
1536/15000 [==>...........................] - ETA: 41s - loss: 0.6771 - acc: 0.5632
2048/15000 [===>..........................] - ETA: 30s - loss: 0.6726 - acc: 0.5708
2560/15000 [====>.........................] - ETA: 23s - loss: 0.6591 - acc: 0.6121
3072/15000 [=====>........................] - ETA: 18s - loss: 0.6472 - acc: 0.6328
3584/15000 [======>.......................] - ETA: 15s - loss: 0.6357 - acc: 0.6551
4096/15000 [=======>......................] - ETA: 13s - loss: 0.6258 - acc: 0.6641
4608/15000 [========>.....................] - ETA: 11s - loss: 0.6206 - acc: 0.6691
5120/15000 [=========>....................] - ETA: 9s - loss: 0.6090 - acc: 0.6779
5632/15000 [==========>...................] - ETA: 8s - loss: 0.5998 - acc: 0.6919
6144/15000 [===========>..................] - ETA: 7s - loss: 0.5899 - acc: 0.7020
6656/15000 [============>.................] - ETA: 6s - loss: 0.5837 - acc: 0.7090
7168/15000 [=============>................] - ETA: 5s - loss: 0.5754 - acc: 0.7153
7680/15000 [==============>...............] - ETA: 5s - loss: 0.5674 - acc: 0.7230
8192/15000 [===============>..............] - ETA: 4s - loss: 0.5622 - acc: 0.7266
8704/15000 [================>.............] - ETA: 3s - loss: 0.5551 - acc: 0.7330
9216/15000 [=================>............] - ETA: 3s - loss: 0.5485 - acc: 0.7396
9728/15000 [==================>...........] - ETA: 3s - loss: 0.5429 - acc: 0.7457
10240/15000 [===================>..........] - ETA: 2s - loss: 0.5354 - acc: 0.7509
10752/15000 [====================>.........] - ETA: 2s - loss: 0.5294 - acc: 0.7557
11264/15000 [=====================>........] - ETA: 1s - loss: 0.5230 - acc: 0.7607
11776/15000 [======================>.......] - ETA: 1s - loss: 0.5162 - acc: 0.7655
12288/15000 [=======================>......] - ETA: 1s - loss: 0.5106 - acc: 0.7687
12800/15000 [========================>.....] - ETA: 1s - loss: 0.5047 - acc: 0.7730
13312/15000 [=========================>....] - ETA: 0s - loss: 0.5017 - acc: 0.7741
13824/15000 [==========================>...] - ETA: 0s - loss: 0.4987 - acc: 0.7765
14336/15000 [===========================>..] - ETA: 0s - loss: 0.4944 - acc: 0.7795
14848/15000 [============================>.] - ETA: 0s - loss: 0.4896 - acc: 0.7828
15000/15000 [==============================] - 8s 513us/step - loss: 0.4879 - acc: 0.7841
- val_loss: 0.3425 - val_acc: 0.8788
Epoch 20/20
512/15000 [>.............................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
1024/15000 [=>............................] - ETA: 1s - loss: 0.0013 - acc: 1.0000
1536/15000 [==>...........................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
2048/15000 [===>..........................] - ETA: 1s - loss: 0.0016 - acc: 1.0000
2560/15000 [====>.........................] - ETA: 1s - loss: 0.0016 - acc: 1.0000
3072/15000 [=====>........................] - ETA: 1s - loss: 0.0016 - acc: 1.0000
3584/15000 [======>.......................] - ETA: 1s - loss: 0.0016 - acc: 1.0000
4096/15000 [=======>......................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
4608/15000 [========>.....................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
5120/15000 [=========>....................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
5632/15000 [==========>...................] - ETA: 1s - loss: 0.0015 - acc: 1.0000
6144/15000 [===========>..................] - ETA: 0s - loss: 0.0014 - acc: 1.0000
6656/15000 [============>.................] - ETA: 0s - loss: 0.0014 - acc: 1.0000
7168/15000 [=============>................] - ETA: 0s - loss: 0.0014 - acc: 1.0000
7680/15000 [==============>...............] - ETA: 0s - loss: 0.0014 - acc: 1.0000
8192/15000 [===============>..............] - ETA: 0s - loss: 0.0014 - acc: 1.0000
8704/15000 [================>.............] - ETA: 0s - loss: 0.0014 - acc: 1.0000
9216/15000 [=================>............] - ETA: 0s - loss: 0.0017 - acc: 0.9999
9728/15000 [==================>...........] - ETA: 0s - loss: 0.0017 - acc: 0.9999
10240/15000 [===================>..........] - ETA: 0s - loss: 0.0017 - acc: 0.9999
10752/15000 [====================>.........] - ETA: 0s - loss: 0.0016 - acc: 0.9999
11264/15000 [=====================>........] - ETA: 0s - loss: 0.0016 - acc: 0.9999
11776/15000 [======================>.......] - ETA: 0s - loss: 0.0016 - acc: 0.9999
12288/15000 [=======================>......] - ETA: 0s - loss: 0.0016 - acc: 0.9999
12800/15000 [========================>.....] - ETA: 0s - loss: 0.0016 - acc: 0.9999
13312/15000 [=========================>....] - ETA: 0s - loss: 0.0016 - acc: 0.9999
13824/15000 [==========================>...] - ETA: 0s - loss: 0.0016 - acc: 0.9999
14336/15000 [===========================>..] - ETA: 0s - loss: 0.0016 - acc: 0.9999
14848/15000 [============================>.] - ETA: 0s - loss: 0.0016 - acc: 0.9999
15000/15000 [==============================] - 3s 170us/step - loss: 0.0016 - acc: 0.9999
- val_loss: 0.7605 - val_acc: 0.8631
在20次训练后,准确率为86.31%。
我们来看看历史纪录打印出的值看看是否发生了过拟合:
history = {
'val_loss': [0.3797392254829407, 0.300249081659317, 0.3083435884475708, 0.283885223865509, 0.2847259536743164, 0.3144310226917267, 0.31279232678413393, 0.38592003211975096, 0.36343686447143553, 0.3843619570732117, 0.4167306966781616, 0.45070800895690916, 0.46998676981925963, 0.502394838142395, 0.5363822244167328, 0.572349524307251, 0.6167236045837402, 0.6382174592018127, 0.7905949376106263, 0.7077673551559448],
'val_acc': [0.8683999997138977, 0.8898000004768372, 0.8715000001907348, 0.8831000001907349, 0.8867000002861023, 0.8772999998092651, 0.8844999999046326, 0.8650999998092651, 0.8783000001907348, 0.8790000001907349, 0.8768999999046325, 0.8692999998092651, 0.8731999997138977, 0.8721999996185302, 0.8688999997138978, 0.8694999996185303, 0.8648999995231629, 0.8663999996185303, 0.8495000007629394, 0.8646999994277954],
'loss': [0.5085020663420359, 0.30055405753453573, 0.2179573760588964, 0.1750892378250758, 0.1426703708012899, 0.11497294256687164, 0.09784598382711411, 0.08069058032830556, 0.06599647818009059, 0.055482132176558174, 0.045179014571507775, 0.038426268839836124, 0.029788546661535898, 0.02438261934618155, 0.0176644352838397, 0.016922697043418884, 0.009341424687206746, 0.011814989059666792, 0.005609988443056742, 0.005509983973701795],
'acc': [0.7815333335240682, 0.9044666666984558, 0.9285333332697551, 0.9436666668891907, 0.954333333047231, 0.9652000000635783, 0.9706666668256124, 0.9762666667938232, 0.9821333333015442, 0.9851333333015442, 0.9887333332379659, 0.9912000002543131, 0.9928666666666667, 0.9948666666666667, 0.9978666666666667, 0.9970000001589457, 0.9994, 0.9974666666666666, 0.9998000002543131, 0.9996666666666667]
}
前两个参数,‘val_loss’和’val_acc’就是测试集的效果,在第二轮训练的时候,准确率达到0.8898,但最后一次训练却只有0.86.这明显发生了过拟合,我们来画出训练集和测试集loss变化曲线,以供进一步分析。
import matplotlib.pyplot as plt
history_dict = {
'val_loss': [0.3797392254829407, 0.300249081659317, 0.3083435884475708, 0.283885223865509, 0.2847259536743164, 0.3144310226917267, 0.31279232678413393, 0.38592003211975096, 0.36343686447143553, 0.3843619570732117, 0.4167306966781616, 0.45070800895690916, 0.46998676981925963, 0.502394838142395, 0.5363822244167328, 0.572349524307251, 0.6167236045837402, 0.6382174592018127, 0.7905949376106263, 0.7077673551559448],
'val_acc': [0.8683999997138977, 0.8898000004768372, 0.8715000001907348, 0.8831000001907349, 0.8867000002861023, 0.8772999998092651, 0.8844999999046326, 0.8650999998092651, 0.8783000001907348, 0.8790000001907349, 0.8768999999046325, 0.8692999998092651, 0.8731999997138977, 0.8721999996185302, 0.8688999997138978, 0.8694999996185303, 0.8648999995231629, 0.8663999996185303, 0.8495000007629394, 0.8646999994277954],
'loss': [0.5085020663420359, 0.30055405753453573, 0.2179573760588964, 0.1750892378250758, 0.1426703708012899, 0.11497294256687164, 0.09784598382711411, 0.08069058032830556, 0.06599647818009059, 0.055482132176558174, 0.045179014571507775, 0.038426268839836124, 0.029788546661535898, 0.02438261934618155, 0.0176644352838397, 0.016922697043418884, 0.009341424687206746, 0.011814989059666792, 0.005609988443056742, 0.005509983973701795],
'acc': [0.7815333335240682, 0.9044666666984558, 0.9285333332697551, 0.9436666668891907, 0.954333333047231, 0.9652000000635783, 0.9706666668256124, 0.9762666667938232, 0.9821333333015442, 0.9851333333015442, 0.9887333332379659, 0.9912000002543131, 0.9928666666666667, 0.9948666666666667, 0.9978666666666667, 0.9970000001589457, 0.9994, 0.9974666666666666, 0.9998000002543131, 0.9996666666666667]
}
loss_values = history_dict['loss'] # 训练集loss
val_loss_values = history_dict['val_loss'] # 测试集loss
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
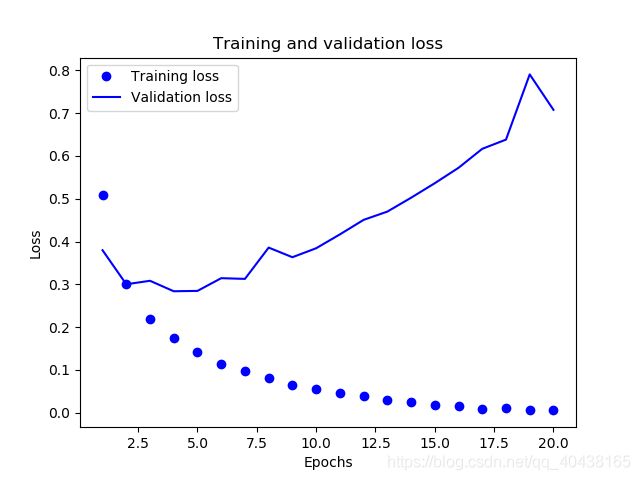
可以看出,训练集loss不断减小,而测试集loss却在增长,发生了过拟合。
为确定我们的判断,我们再画出训练集和测试集的准确率看看:
import matplotlib.pyplot as plt
history_dict = {
'val_loss': [0.3797392254829407, 0.300249081659317, 0.3083435884475708, 0.283885223865509, 0.2847259536743164, 0.3144310226917267, 0.31279232678413393, 0.38592003211975096, 0.36343686447143553, 0.3843619570732117, 0.4167306966781616, 0.45070800895690916, 0.46998676981925963, 0.502394838142395, 0.5363822244167328, 0.572349524307251, 0.6167236045837402, 0.6382174592018127, 0.7905949376106263, 0.7077673551559448],
'val_acc': [0.8683999997138977, 0.8898000004768372, 0.8715000001907348, 0.8831000001907349, 0.8867000002861023, 0.8772999998092651, 0.8844999999046326, 0.8650999998092651, 0.8783000001907348, 0.8790000001907349, 0.8768999999046325, 0.8692999998092651, 0.8731999997138977, 0.8721999996185302, 0.8688999997138978, 0.8694999996185303, 0.8648999995231629, 0.8663999996185303, 0.8495000007629394, 0.8646999994277954],
'loss': [0.5085020663420359, 0.30055405753453573, 0.2179573760588964, 0.1750892378250758, 0.1426703708012899, 0.11497294256687164, 0.09784598382711411, 0.08069058032830556, 0.06599647818009059, 0.055482132176558174, 0.045179014571507775, 0.038426268839836124, 0.029788546661535898, 0.02438261934618155, 0.0176644352838397, 0.016922697043418884, 0.009341424687206746, 0.011814989059666792, 0.005609988443056742, 0.005509983973701795],
'acc': [0.7815333335240682, 0.9044666666984558, 0.9285333332697551, 0.9436666668891907, 0.954333333047231, 0.9652000000635783, 0.9706666668256124, 0.9762666667938232, 0.9821333333015442, 0.9851333333015442, 0.9887333332379659, 0.9912000002543131, 0.9928666666666667, 0.9948666666666667, 0.9978666666666667, 0.9970000001589457, 0.9994, 0.9974666666666666, 0.9998000002543131, 0.9996666666666667]
}
loss_values = history_dict['acc'] # 训练集loss
val_loss_values = history_dict['val_acc'] # 测试集loss
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training acc')
plt.plot(epochs, val_loss_values, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
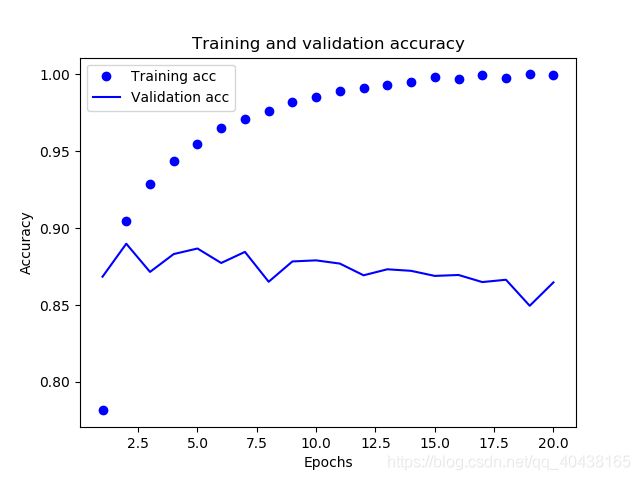
训练集准确率不断上升,而测试集准确率却波澜起伏,在最后几次不断下降,明显发生过拟合。遇到这种情况我们需要采取一些措施,最简单的就是少训练几轮,当然还有更多方法,比如正则化,dropout等等,以后会讨论。