Distributed Stochastic Gradient Method for Non-Convex Problems with Applications in Supervised Learn

Distributed Stochastic Gradient Method for Non-Convex Problems with Applications in Supervised Learning

Abstract

We develop a distributed stochastic gradient descent algorithm for solving non-convex optimization problems under the assumption that the local objective functions are twice continuously differentiable with Lipschitz continuous gradients and Hessians. We provide sufficient conditions on step-sizes that guarantee the asymptotic mean-square convergence of the proposed algorithm. We apply the developed algorithm to a distributed supervised-learning problem, in which a set of networked agents collaboratively train their individual neural nets to recognize handwritten digits in images. Results indicate that all agents report similar performance that is also comparable to the performance of a centrally trained neural net. Numerical results also show that the proposed distributed algorithm allows the individual agents to recognize the digits even though the training data corresponding to all the digits is not locally available to each agent.

在局部目标函数与Lipschitz连续梯度和Hessian连续两次可微的假设下，我们开发了一种求解非凸优化问题的分布式随机梯度下降算法。 我们在步长上提供足够的条件，以保证所提出算法的渐近均方收敛。 我们将开发的算法应用于分布式监督学习问题，在该问题中，一组网络代理协作训练他们各自的神经网络，以识别图像中的手写数字。 结果表明，所有代理均报告了相似的性能，也与集中训练的神经网络的性能相当。 数值结果还表明，即使不是所有代理都本地可用的训练数据，所提出的分布式算法也允许单个代理识别数字。

I. INTRODUCTION

With the advent of smart devices, there has been an exponential growth in the amount of data collected and stored locally on the individual devices. Applying machine learning to extract value from such massive data to provide data-driven insights, decisions, and predictions has been a hot research topic as well as the focus of numerous businesses like Google, Facebook, Alibaba, Yahoo, etc. However, porting these vast amounts of data to a data center to conduct traditional machine learning has raised two main issues: (i) the communication challenge associated with transferring vast amounts of data from a large number of devices to a central location and (ii) the privacy issues associated with sharing raw data. Distributed machine learning techniques based on the server-client architecture [1], [2] have been proposed as solutions to this problem. On one extreme end of this architecture, we have the parameter server approach, where a server or group of servers initiate distributed learning by pushing the current model to a set of client nodes that host the data. Client nodes compute the local gradients or parameter updates and communicate it to the server nodes. Server nodes aggregate these values and update the current model [3], [4]. On the other extreme, we have federated learning, where each client node obtains a local solution to the learning problem and the server node computes a global model by simply averaging the local models [5], [6]. These distributed learning techniques are not truly distributed since they follow a master-slave architecture and do not involve any peer-to-peer communication. Though these techniques are not always robust and they are rendered useless if the server fails, they do provide a good business opportunity for companies that own servers and host web services. However, our aim is to develop a fully distributed machine learning architecture enabled by client-to-client interaction.

随着智能设备的出现，本地收集和存储在各个设备上的数据量呈指数增长。应用机器学习从海量数据中提取价值以提供数据驱动的见解，决策和预测一直是研究的热点，也是Google，Facebook，阿里巴巴，雅虎等众多企业关注的焦点。但是，将这些移植大量数据传输到数据中心以进行传统的机器学习提出了两个主要问题：（i）与将大量数据从大量设备传输到中心位置相关的通信挑战，以及（ii）相关的隐私问题与共享原始数据。已经提出了基于服务器-客户端体系结构[1]，[2]的分布式机器学习技术作为该问题的解决方案。在此架构的一个极端中，我们采用了参数服务器方法，其中一台服务器或一组服务器通过将当前模型推送到托管数据的一组客户端节点来启动分布式学习。客户端节点计算局部梯度或参数更新，并将其传达给服务器节点。服务器节点汇总这些值并更新当前模型[3]，[4]。在另一种极端情况下，我们进行了联合学习，其中每个客户端节点都获得了针对学习问题的本地解决方案，而服务器节点则通过简单地对本地模型进行平均来计算全局模型[5]，[6]。这些分布式学习技术不是真正的分布式，因为它们遵循主从结构，并且不涉及任何对等通信。尽管这些技术并不总是很可靠，如果服务器发生故障，它们将变得无用，但它们确实为拥有服务器和托管Web服务的公司提供了良好的商机。但是，我们的目标是开发一种通过客户端到客户端交互实现的完全分布式的机器学习架构。

For large-scale machine learning, stochastic gradient descent (SGD) methods are often preferred over batch gradient methods [7] because (i) in many large-scale problems, there is a good deal of redundancy in data and therefore it is inefficient to use all the data in every optimization iteration, (ii) the computational cost involved in computing the batch gradient is much higher than that of the stochastic gradient, and (iii) stochastic methods are more suitable for online learning where data are arriving sequentially. Since most machine learning problems are non-convex, there is a need for distributed stochastic gradient methods for non-convex problems. Therefore, here we present a distributed stochastic gradient algorithm for non-convex problems and demonstrate its utility for distributed machine learning. A few early examples of (non-stochastic or deterministic) distributed non-convex optimization algorithms include the Distributed Approximate Dual Subgradient (DADS) Algorithm [8], NonconvEx primal-dual SpliTTing (NESTT) algorithm [9], and the Proximal Primal-Dual Algorithm (Prox-PDA) [10]. More recently, a non-convex version of the accelerated distributed augmented Lagrangians (ADAL) algorithm is presented in [11] and successive convex approximation (SCA)-based algorithms such as iNner cOnVex Approximation (NOVA) and in-Network succEssive conveX approximaTion algorithm (NEXT) are given in [12] and [13], respectively. References [14]–[16] provide several distributed alternating direction method of multipliers (ADMM) based non-convex optimization algorithms. Non-convex versions of Decentralized Gradient Descent (DGD) and Proximal Decentralized Gradient Descent (Prox-DGD) are given in [17]. Finally, Zeroth-Order NonconvEx (ZONE) optimization algorithms for mesh network (ZONE-M) and star network (ZONE-S) are presented in [18].

对于大规模机器学习，随机梯度下降（SGD）方法通常优于批量梯度方法[7]，因为（i）在许多大规模问题中，数据存在大量冗余，因此，效率低下在每次优化迭代中都使用所有数据，（ii）计算批次梯度所涉及的计算成本比随机梯度要高得多，并且（iii）随机方法更适合于数据按顺序到达的在线学习。由于大多数机器学习问题是非凸的，因此需要用于非凸问题的分布式随机梯度方法。因此，在这里，我们提出了一种针对非凸问题的分布式随机梯度算法，并展示了其在分布式机器学习中的效用。早期（非随机或确定性）分布式非凸优化算法的一些示例包括分布式近似双子梯度（DADS）算法[8]，NonconvEx原始对偶拆分（NESTT）算法[9]和近邻原始-双重算法（Prox-PDA）[10]。最近，[11]中提出了加速分布的增强拉格朗日算法（ADAL）的非凸版本以及基于连续凸逼近（SCA）的算法，例如iNner cOnVex逼近（NOVA）和网络内成功对凸逼近算法（NEXT）分别在[12]和[13]中给出。参考文献[14]-[16]提供了几种基于乘法器的分布式交替方向方法（ADMM），基于非凸优化算法。分散梯度下降（DGD）和近端分散梯度下降（Prox-DGD）的非凸版本在[17]中给出。最后，在[18]中提出了网格网络（ZONE-M）和星型网络（ZONE-S）的零阶非ConvEx（ZONE）优化算法。

There exist several works on distributed stochastic gradient methods, but mainly for strongly convex optimization problems. These include the stochastic subgradient-push method for distributed optimization over time-varying directed graphs given in [19], distributed stochastic optimization over random networks given in [20], the Stochastic Unbiased Curvatureaided Gradient (SUCAG) method given in [21], and distributed stochastic gradient tracking methods [22]. There are very few works on distributed stochastic gradient methods for nonconvex optimization [23], [24]; however, they make very restrictive assumptions on the critical points of the problem. Contributions of this paper are three-fold: 1) We propose a fully distributed machine learning architecture that does not require any server nodes. 2) We develop a distributed SGD algorithm and provide sufficient conditions on step-sizes such that the algorithm is mean-square convergent. 3) We demonstrate the utility of the proposed SGD algorithm for distributed machine learning.

关于分布式随机梯度法，已有一些著作，但主要针对强凸优化问题。这些包括[19]中给出的用于时变有向图的分布优化的随机次梯度推方法，[20]中给出的在随机网络上的分布随机优化，[21]中给出的随机无偏曲率梯度（SUCAG）方法，和分布式随机梯度跟踪方法[22]。对于非凸优化，关于分布式随机梯度法的工作很少[23]，[24]。但是，他们对问题的关键点做出了非常严格的假设。本文的贡献包括三个方面：1）我们提出了一种不需要任何服务器节点的完全分布式的机器学习架构。 2）我们开发了一种分布式SGD算法，并在步长上提供了充分的条件，以使该算法具有均方收敛性。 3）我们演示了提出的SGD算法在分布式机器学习中的实用性。

A. Notation

II. DISTRIBUTED MACHINE LEARNING

Here Ri(w) denotes the expected risk given a parameter vector w with respect to the probability distribution Pi. The total expected risk across all networked agents is given as
在此，Ri（w）表示相对于概率分布Pi的给定参数向量w的预期风险。 所有联网代理的预期总风险为

DISTRIBUTED SGD

A. Assumptions

First, we state the following assumption on the individual objective functions:

首先，我们针对各个目标函数陈述以下假设：





Assumption 7 is the bounded variance assumption typically make in SGD literature. Finally, it follows from Assumptions 1, 7 and Lemma 1 that the stochastic gradients are bounded, which is usually just assumed in literature [7], [17], [23], [27].

假设7是SGD文献中通常做出的有界方差假设。 最后，从假设1、7和引理1得出，随机梯度是有界的，通常在文献[7]，[17]，[23]，[27]中都假设过。

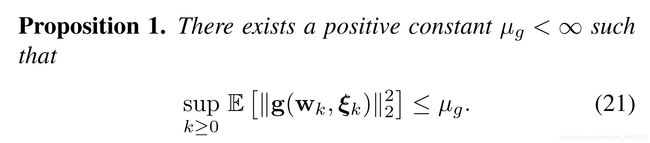
Proof: Proof follows from taking the expectation of (20) and applying the result from Lemma 1.

证明：根据（20）的期望值并应用引理1的结果进行证明。

IV. CONVERGENCE ANALYSIS

Our strategy for proving the convergence of the proposed distributed SGD algorithm to a critical point is as follows. First we show that the consensus error among the agents are diminishing at the rate of
我们用于证明所提出的分布式SGD算法收敛到临界点的策略如下。 首先，我们证明代理之间的共识误差正在以

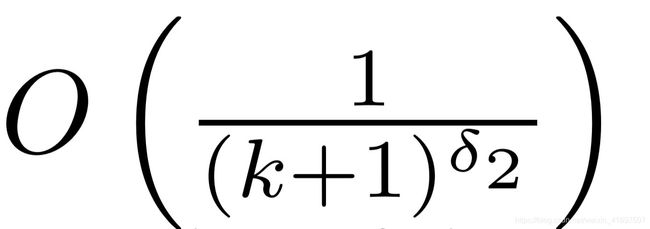
Asymptotic convergence of the algorithm is then proved in Theorem 3. Theorem 4 then establishes that the weighted expected average gradient norm is a summable sequence. Finally, Theorem 5 proves the asymptotic mean-square convergence of the algorithm to a critical point.
Theorem 1. Consider distributed SGD algorithm (8) under Assumptions [1-7]. Then, there holds:
然后在定理3中证明了该算法的渐近收敛性。定理4随后确定了加权期望平均梯度范数为可加序列。 最终，定理5证明了算法的渐近均方收敛到临界点。
定理1.在假设[1-7]下考虑分布式SGD算法（8）。 然后，保持：

Theorem 4 establishes results about the weighted sum of expected average gradient norm and the key takeaway from this result is that, for the distributed SGD in (8) with appropriate step-sizes, the expected average gradient norms cannot stay bounded away from zero (See Theorem 9 of [7]), i.e.,

定理4建立了关于期望平均梯度范数的加权和的结果，并且从这个结果中得出的主要结论是，对于（8）中具有适当步长的分布式SGD，期望的平均梯度范数不能保持远离零的界限（参见 [7]的定理9），即

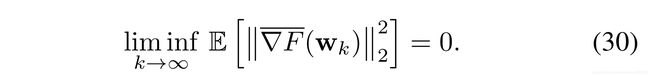
Finally, we present the following result to illustrate that stronger convergence results follows from the continuity assumption on the Hessian, which has not been utilized in our analysis so far.

最后，我们给出以下结果以说明更强的收敛结果来自对Hessian的连续性假设，该假设到目前为止尚未在我们的分析中使用。

Remark 1. Similar to the centralized SGD [7], the analysis given here shows the mean-square convergence of the distributed algorithm to a critical point, which include the saddle points. Though SGD has shown to escape saddle points efficiently [28]–[30], extension of such results for distributed SGD is currently nonexistent and is the topic of future research.

备注1.与集中式SGD [7]相似，此处给出的分析显示了分布式算法到临界点的均方收敛，其中包括鞍点。 尽管SGD已经证明可以有效地避开鞍点[28] – [30]，但是对于分布式SGD来说，这种结果的扩展目前尚不存在，并且是未来研究的主题。

APPLICATION TO DISTRIBUTED SUPERVISED LEARNING

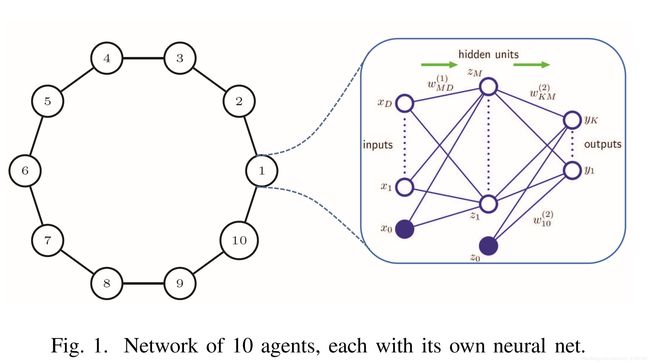
We apply the proposed algorithm for distributedly training 10 different neural nets to recognize handwritten digits in images. Specifically, we consider a subset of the MNIST1 data set containing 5000 images of 10 digits (0-9), of which 2500 are used for training and 2500 are used for testing.
我们将提出的算法应用于10种不同的神经网络的分布式训练，以识别图像中的手写数字。 具体来说，我们考虑MNIST1数据集的一个子集，其中包含5000张10位（0-9）图像，其中2500张用于训练，2500张用于测试。

Training data are divided among ten agents connected in an undirected unweighted ring topology (see Fig. 1). Each agent aims to train its own neural network consisting of a single hidden layer of 50 neurons (51 including the bias neuron). Since the images are 20 × 20, the input layer consists of 401 neurons (including the one bias neuron) and the output later consists of 10 neurons, one for each output class, i.e., one for each digits 0-9. As shown in Fig. 1, for each agent, the neural net consists

训练数据被划分为十个以无向非加权环形拓扑连接的代理（见图1）。 每个代理旨在训练自己的神经网络，该网络由50个神经元（包括偏置神经元的51个）的单个隐藏层组成。 由于图像为20×20，因此输入层由401个神经元（包括一个偏置神经元）组成，后来的输出由10个神经元组成，每个输出类别一个，即每个数字0-9对应一个。 如图1所示，对于每个代理，神经网络由

Taking the negative logarithm of the corresponding likelihood function yields the following empirical risk function:

取相应似然函数的负对数可得出以下经验风险函数：

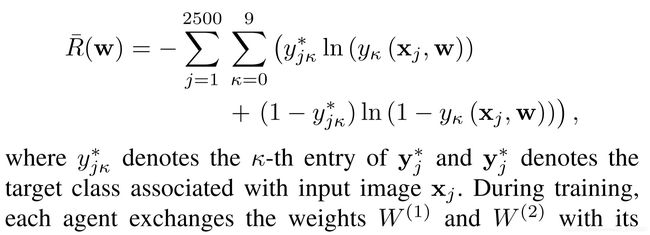
neighbors as described in the proposed algorithm. Here we conduct the following three experiments: (i) centralized SGD, where a centralized version of the SGD is implemented by a central node having all 2500 training data, (ii) a distributed SGD depicted in Fig. 1 with equally distributed data, where 10 agents distributedly train 10 different neural nets, and (iii) a distributed SGD with class-specific data distributed among the agents. For experiment (ii), each node received 250 training data, randomly sampled from the entire training set, i.e., mi = 250 for all i = 1,…,10. For experiment (iii), data are distributed such that each agent only receives images corresponding to a particular class, i.e., agent 1 received all the images of 0s, agent 2 received all the images of 1s,

所提出算法中描述的邻居。 在这里，我们进行以下三个实验：（i）集中式SGD，其中SGD的集中式版本是由具有所有2500个训练数据的中央节点实现的；（ii）图1中所示的分布式SGD具有均等的分布数据，其中 10个代理分布式训练10个不同的神经网络，以及（iii）分布式SGD，其中在代理之间分布有类别特定的数据。 对于实验（ii），每个节点接收250个训练数据，这些数据是从整个训练集中随机采样的，即对于所有i = 1，…，10，mi = 250。 对于实验（iii），数据被分配为使得每个代理仅接收对应于特定类别的图像，即代理1接收所有0的图像，代理2接收所有1的图像，


Given in Fig. 2 are the results obtained from the three experiments. The risks obtained from experiments (i), (ii),
and (iii) are given in Figs. 2(a), 2(b), and 2©, respectively. For all three experiments, the error rate, i.e., % of images misclassified, obtained from running the trained neural net on the testing data of 2500 images are Experiments (i): 7.12%, (ii): 7.36%, (iii): 7.36%
Finally, a few misclassification examples are given in Fig. 2(d), where a 7 is misclassified as a 5, 2 as a 4, and so forth. Results given here indicate that regardless of how the data are distributed, the agents are able to train their network and the distributedly trained networks are able to yield similar performance as that of a centrally trained network. More importantly, in experiment (iii), agents were able to recognize all 10 classes even though they only had access to data corresponding to a single class. This result has numerous implications for the machine learning community, specifically for federated multitask learning under information flow constraints.

图2中给出的是从这三个实验中获得的结果。实验（i），（ii），和（iii）在图1和2中给出。图2（a），2（b）和2（c）。对于所有三个实验，通过对2500个图像的测试数据运行训练的神经网络而获得的错误率（即，错误分类的图像的百分比）为实验（i）：7.12％，（ii）：7.36％，（iii）： 7.36％
最后，在图2（d）中给出了一些错误分类的示例，其中7被错误分类为5，2被错误分类为4，依此类推。此处给出的结果表明，无论数据如何分配，代理都可以训练其网络，而分布式训练的网络则可以产生与集中训练的网络类似的性能。更重要的是，在实验（iii）中，即使代理商只能访问与单个类别相对应的数据，他们也能够识别所有10个类别。这个结果对机器学习社区有很多影响，特别是在信息流约束下的联合多任务学习。

VI. CONCLUSION

This paper presented the development of a distributed stochastic gradient descent algorithm for solving non-convex optimization problems. Here we assumed that the local objective functions are Lipschitz continuous and twice continuously differentiable with Lipschitz continuous gradients and Hessians. We provided sufficient conditions on algorithm step-sizes that guarantee asymptotic mean-square convergence of the proposed algorithm to a critical point. We applied the developed algorithm to a distributed supervised-learning problem, in which a set of 10 networked agents collaboratively train their individual neural nets to recognize handwritten digits in images. Results indicate that regardless of how the data are distributed, the agents are able to train their network and the distributedly trained networks are able to yield similar performance as that of a centrally trained network. Numerical results also show that the proposed distributed algorithm allowed individual agents to collaboratively recognize all 10 classes even though they only had access to data corresponding to a single class.

本文提出了一种求解非凸优化问题的分布式随机梯度下降算法。在这里，我们假设局部目标函数是Lipschitz连续的，并且与Lipschitz连续梯度和Hessian连续两次可微。我们在算法步长上提供了充分的条件，以保证所提出算法的渐近均方收敛到临界点。我们将开发的算法应用于分布式监督学习问题，在该问题中，一组10个网络代理共同协作训练其各自的神经网络，以识别图像中的手写数字。结果表明，无论数据如何分配，代理都可以训练其网络，而分布式训练的网络则可以产生与集中训练的网络类似的性能。数值结果还表明，提出的分布式算法允许单个代理协同识别所有10个类别，即使它们只能访问与单个类别相对应的数据也是如此。

APPENDIX

A. Useful Lemmas