带权二分/wqs二分/凸优化入门——由【HYSBZ 4518】征途引入的对函数意义理解和二分、斜率优化细节的讨论
天幕
- 引入
- 真正的引入
- 正解
- 感性理解
- 真正的分析
- 再说一点
- 代码
- HYSBZ 4518征途题解
- 题目描述
- 题解
- 小知识点:确定斜率优化的方法
- 小知识点:对二分细节的讨论
- 普适方法介绍
- 二分模板
- 代码
- 总结
引入
先来一段的总结(引用自讲课ppt),希望可以在各位阅读后再回头看时带来更深的理解。
“带权二分描述了二分的过程,“凸优化”揭示了算法的本质,而“wqs二分”阐明了算法的发现人。
这也是这篇博客内容的核心。
这篇博客先暂未讨论二分的精度问题,说不定未来的某一天会补上
特别鸣谢:
强大的几何画板& KaTeX \KaTeX KATEX之神MiMiZhaner
沉迷讨论的LSK
真正的引入
一个简单的题目: n n n个点, m m m条边,每条边有颜色(黑或白)和边权,求恰好含 k k k条白边的最小生成树。
正解
这里必然会出现些妖魔鬼怪的做法,或对或错我们不予讨论。
既然是引入,便直接上一下有关这个算法的正解。
我们对每条白边添加一个附加边权,再做一个最小生成树,这样就可以限制所选白边的数量。我们二分这个附加边权,每次统计所选白边数量,直到所选数量为m。
二分的单调性是显然的对吧。
感性理解
正确性反正就是很可以理解对吧。
呃,附加边权越大所选白边越小的单调性也可以感受对吧。
好像不太感性吧。
真正的分析
虽然这道题不太需要,但为了后面一道题,先大概讲一下。
下面是一段不负责任的分析。
记 f ( x ) f(x) f(x)为选 x x x条白边的最小生成树权值和。(不考虑附加权值,不管是怎么求出来的)
可以比较理性的发现, f ( x ) f(x) f(x)长这样

技艺粗糙,大概理解一下吧。
这就是所谓的凸函数。
为了便于理解,我们令这时最小生成树的权值和为 b m i n b_{min} bmin(这是计算了附加权值的)。
这道题目中,我们可以从两个角度来理解:
(1)可以简单地理解为用附加权值 C C C来限制白边数量但不实际计算附加权值;
(2)令 g ( x , C ) g(x,C) g(x,C)表示附加权值为 C C C时选取 x x x条白边的最小生成树(实际计算附加权值),这个别管我们怎么算的。非常显然的是它跟上一个不管是怎么求出来的东西的关系: g ( x , C ) = f ( x ) + C ⋅ x g(x,C)=f(x)+C·x g(x,C)=f(x)+C⋅x
那么对于一个 C C C必然会有一个最小的 g ( x , C ) g(x,C) g(x,C)
令对于一个附加权值 C C C,我们就找到此时的最优决策点 x 0 x_0 x0
并且 f ( x ) = − C ⋅ x + g ( x , C ) f(x)=-C·x+g(x,C) f(x)=−C⋅x+g(x,C)
以及
f ( x 0 ) = − C ⋅ x 0 + g ( x , C ) m i n f(x_0)=-C·x_0+g(x,C)_{min} f(x0)=−C⋅x0+g(x,C)min
我们可以理解为是由 f ( x ) , C f(x),C f(x),C共同影响得到了 g ( x , C ) m i n g(x,C)_{min} g(x,C)min
形象的说就是 f ( x ) f(x) f(x)上的点对应一个 g ( x , C ) g(x,C) g(x,C),去找让 g ( x , C ) g(x,C) g(x,C)最小的 x x x,而 g ( x , C ) g(x,C) g(x,C)就是过 ( x , f ( x ) ) (x,f(x)) (x,f(x))过一点做一条斜率为 − C -C −C的直线与 y y y轴的交点。
可以抽象成一个简单的数学题目:给一个凸函数 f ( x ) f(x) f(x),一条过 f ( x ) f(x) f(x)上点的直线的斜率 − C -C −C,求此时该直线最小截距。
那么很显然此时的 y = − C ⋅ x + g ( x , C ) m i n y=-C·x+g(x,C)_{min} y=−C⋅x+g(x,C)min就是 f ( x ) f(x) f(x)的切线。
⋯ ⋯ \cdots\cdots ⋯⋯呃,为了吸引 方便读者,放个图解释一下为什么是切线吧:

非常明显的是 A A A是最小的。
并且从这个式子 f ( x ) = − C ⋅ x + g ( n , C ) f(x)=-C·x+g(n,C) f(x)=−C⋅x+g(n,C)
可知我们只需要让 x = m x=m x=m,就能得到此时的 f ( x ) f(x) f(x)。于是不断二分 C C C,影响 x x x使其逼近 m m m。
而且我们想象一下当斜率不断增大,这个切点是在不断右移的,这也进一步说明了二分的正确性。
好了,已经入门了。
再说一点
可以发现的是对于每一个 C C C所算的 g ( n , C ) g(n,C) g(n,C)本应该是互相独立并且受 C C C实际影响的,为什么这道题里我们可以不实际算 C C C呢?
因为 K r u s k a l Kruskal Kruskal是一个贪心算法,它对每一个 C C C的转移方法都是一样的,附加权值只影响加边的顺序。
而在大多数题目中,如果不实际计算附加权值是无法进行正确的转移和限定的。
代码
没有实际算附加权值
/*Wiz_HUA*/
#includeHYSBZ 4518征途题解
以及对二分的讨论和斜率优化的补充
题目描述
Pine开始了从 S S S地到 T T T地的征途。
从 S S S地到 T T T地的路可以划分成n段,相邻两段路的分界点设有休息站。
Pine计划用m天到达T地。除第m天外,每一天晚上Pine都必须在休息站过夜。所以,一段路必须在同一天中走完。
Pine希望每一天走的路长度尽可能相近,所以他希望每一天走的路的长度的方差尽可能小。
帮助Pine求出最小方差是多少。
设方差是v,可以证明, v × m 2 v×m^2 v×m2是一个整数。为了避免精度误差,输出结果时输出 v × m 2 v×m^2 v×m2。
题解
化简…本来想省略了
p p p是每一段路程的平均数, s 2 s^2 s2是方差, S S S是总距离
{ S = ∑ x i = m ⋅ p p = ∑ x i m s 2 = ∑ ( x i − p ) 2 m a n s = s 2 ⋅ m 2 \begin{cases} S={\sum{x_i}}=m·p\\\\ p=\dfrac{\sum{x_i}}{m}\\\\ s^2=\dfrac{\sum{(x_i-p)^2}}{m}\\\\ ans=s^2·m^2 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧S=∑xi=m⋅pp=m∑xis2=m∑(xi−p)2ans=s2⋅m2
m ⋅ s 2 = ∑ ( x i − p ) 2 = ∑ x i 2 + m ⋅ p 2 − 2 p ⋅ ∑ x i = ∑ x i 2 + m ⋅ p 2 − 2 m ⋅ p 2 = ∑ x i 2 − m ⋅ p 2 \begin{aligned} m·s^2&= \sum{(x_i-p)^2}\\\\ &=\sum{{x_i}^2}+m·p^2-2p·\sum{x_i}\\\\ &=\sum{{x_i}^2}+m·p^2-2m·p^2\\\\ &=\sum{{x_i}^2}-m·p^2 \end{aligned} m⋅s2=∑(xi−p)2=∑xi2+m⋅p2−2p⋅∑xi=∑xi2+m⋅p2−2m⋅p2=∑xi2−m⋅p2
a n s = m ⋅ ∑ x i 2 − S 2 ans=m·\sum{{x_i}^2}-S^2 ans=m⋅∑xi2−S2
显然,我们要求的就是 ∑ x i 2 \sum{{x_i}^2} ∑xi2的最小值。
带权二分给每段加一个权,再求段数没有限制的 min { ∑ x i 2 } \min\{\sum{{x_i}^2}\} min{∑xi2},并处理处最小值的时候的段数。很容易发现加的权越大,这个段数越少;加的权越小,这个段数就越大;那就看这个段数刚好等于 m m m的时候,就是答案了。
为了方便读者感知我们大概讲一下加权与段数的关系(下文讨论凸函数的时候也与此相关)。为了方便我们只讨论一下较特殊的情况,这也是足够说明的。假设有 x 1 , x 2 , x 3 … … x n x_1,x_2,x_3……x_n x1,x2,x3……xn,当附加权值 C C C为0或更小时,显然我们会选择每一个 x x x分一段 ( a + b ) 2 = a 2 + b 2 + 2 a b > a 2 + b 2 (a+b)^2=a^2+b^2+2ab>a^2+b^2 (a+b)2=a2+b2+2ab>a2+b2;但当 C → ∞ C\rightarrow\infty C→∞我们会让所有的 x x x成为一段,那么只会加一个附加权值。
现在的问题就只剩下求段数没有限制的 min { ∑ x i 2 } \min\{\sum{{x_i}^2}\} min{∑xi2}了。
这是一个很easy to know的斜率优化dp。
d p [ i ] dp[i] dp[i]表示前 i i i个数,分成任意段的 min { ∑ x i 2 } \min\{\sum{{x_i}^2}\} min{∑xi2}。
d p [ i ] = min { d p [ j ] + ( d [ i ] − d [ j ] ) 2 + C } ( j < i ) dp[i]=\min\{dp[j]+(d[i]-d[j])^2+C\}\quad(j
怎么说呢,你观察一下数据范围,发现这个东西可以直接暴力,那么下面的斜率优化过程你就可以忽略了。
先推式子。
令 j 1 < j 2 , d [ j 1 ] < d [ j 2 ] , d p [ j 1 ] j_1
d p [ j 1 ] + ( d [ i ] − d [ j 1 ] ) 2 + C < d p [ j 2 ] + ( d [ i ] − d [ j 2 ] ) 2 + C dp[j_1]+(d[i]-d[j_1])^2+C
令 g ( i ) = d p [ i ] + d [ i ] 2 g(i)=dp[i]+d[i]^2 g(i)=dp[i]+d[i]2
则
g ( j 1 ) − g ( j 2 ) < 2 ⋅ d [ i ] ⋅ ( d [ j 1 ] − d [ j 2 ] ) g(j_1)-g(j_2)<2·d[i]·(d[j_1]-d[j_2]) g(j1)−g(j2)<2⋅d[i]⋅(d[j1]−d[j2])
又 d [ j 1 ] − d [ j 2 ] < 0 d[j_1]-d[j_2]<0 d[j1]−d[j2]<0
g ( j 1 ) − g ( j 2 ) d [ j 1 ] − d [ j 2 ] > 2 ⋅ d [ i ] \dfrac{g(j_1)-g(j_2)}{d[j_1]-d[j_2]}>2·d[i] d[j1]−d[j2]g(j1)−g(j2)>2⋅d[i]
这就是斜率式嘛,转移的时候记录一下段数就OK了。
小知识点:确定斜率优化的方法
以这道题目为例,即当 g ( j 1 ) − g ( j 2 ) d [ j 1 ] − d [ j 2 ] > 2 ⋅ d [ i ] \dfrac{g(j_1)-g(j_2)}{d[j_1]-d[j_2]}>2·d[i] d[j1]−d[j2]g(j1)−g(j2)>2⋅d[i], j 1 j_1 j1优于 j 2 j_2 j2
先确定凸包形状
假设是如图的上凸包

此时 K ( j 1 , j 2 ) > k > K ( j 2 , j 3 ) K(j_1,j_2)>k>K(j_2,j_3) K(j1,j2)>k>K(j2,j3),所以 j 1 j1 j1优于 j 2 j2 j2, j 3 j3 j3优于 j 2 j2 j2,而且无论 k k k怎么变化,都至少会有一个比 j 2 j2 j2优,所以 j 2 j2 j2不应该保留,所以上凸包不对。
那么再检验一下下凸包
此时 j 2 j_2 j2比较优,并且显然 j 1 , j 3 j_1,j_3 j1,j3是还可以随 k k k的变化挣扎的,所以就是上凸包。
那么现在分析它维护的是对首还是队尾
可以看以下图示:
可以发现,最初是队首比较优,在这根线的旋转(斜率不断增大)过程中,前面的点逐渐变得不优。所以我们得到:维护队首最优。
小知识点:对二分细节的讨论
首先,我们来画一画这道题目的凸函数,大概是这样。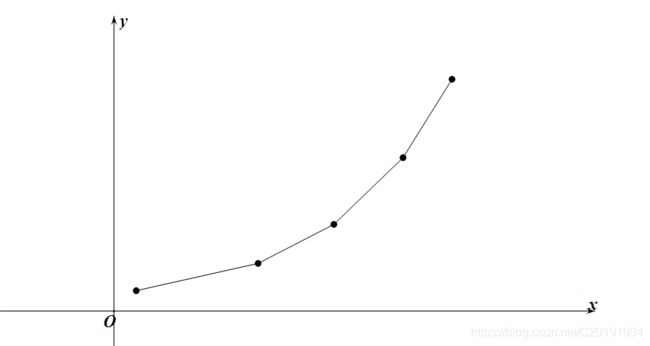
我们仍然发现,它是一个下凸的函数,并且是单调的(虽然没什么用但是就是想说)。画这幅图突出的重点是它是离散的(图中未体现,这是一种下面会讨论的特殊情况)。
这会导致什么呢?可以先自己思考一下。
我们先想一下我们是怎么找到 x = m x=m x=m的:二分斜率,可以形象地看做是旋转一根线往 f ( x ) f(x) f(x)上贴近。类似这样:
因为上面是离散点,所以一个 C C C可能对应着两个点(有同学说可能对应更多个,暂时还没碰倒,因为原本连续f(x)是一个斜率严格上升的下凸包) 我屈服了,就多个吧;也就是两个相邻点的斜率等于 C C C的情况。
那么这个时候我们就会发现存在1个 x x x对应多个 C C C和1个 C C C对应多个 x x x的情况。
这就会可能不存在一个会使我们最后返回的段数为 x = m x=m x=m的 C C C,那怎么稳定地使我们的二分正确呢。
如果你感到没太明白这是在叙述什么情况请在思考一会后勇敢地直接往下看
下面介绍一个普适的方法(鸣谢沉迷讨论的LSK)。
普适方法介绍
前置操作:把一个附加权值的最值看成 b = f ( x ) ± c ⋅ x b=f(x)\pm c·x b=f(x)±c⋅x这样做的意义就是我们可以完全根据 C C C的大小来理解斜率。
以一个下凸函数为例:
先谈一下我对这个用斜率找点的过程的理解,就是用一条线去贴 f ( x ) f(x) f(x),同时我们同样可以把一个斜率放到一个点上去理解。
例如该图中就完全可以用 c n t cnt cnt去反映 C C C这个斜率。
并且我们发现当 C C C变大或变小时 c n t cnt cnt的移动是单调的。
下文的二分都是采用 ( L , R ] (L,R] (L,R],并且对于一个多点共线的斜率 C C C我们找到的是那条直线上最小的 c n t cnt cnt
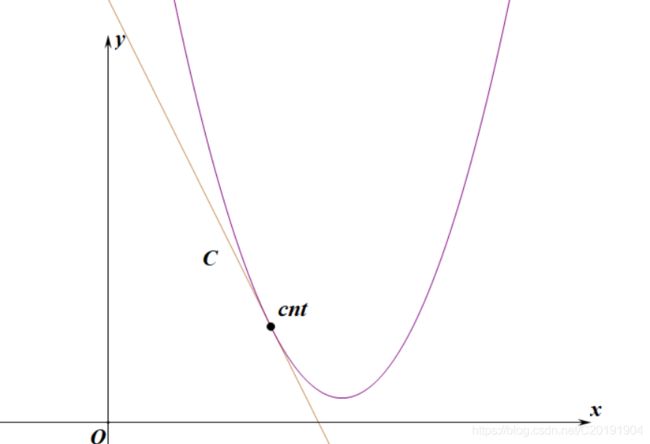
如果在某一次 C h e c k Check Check中我们的 c n t < m cnt
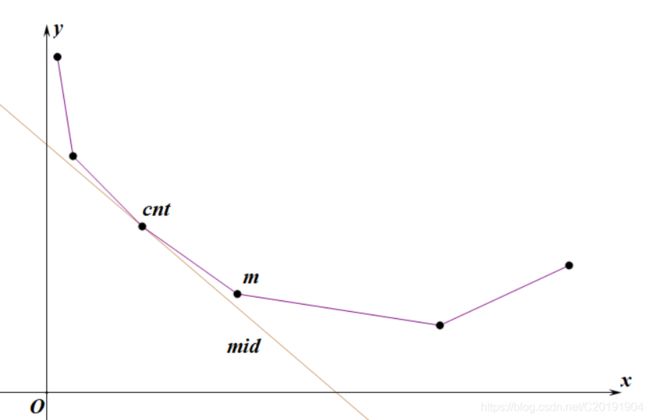
那么与之对应的 c n t > m cnt>m cnt>m 如图所示,那么就应该让线陡一点,即让 L = m i d L=mid L=mid
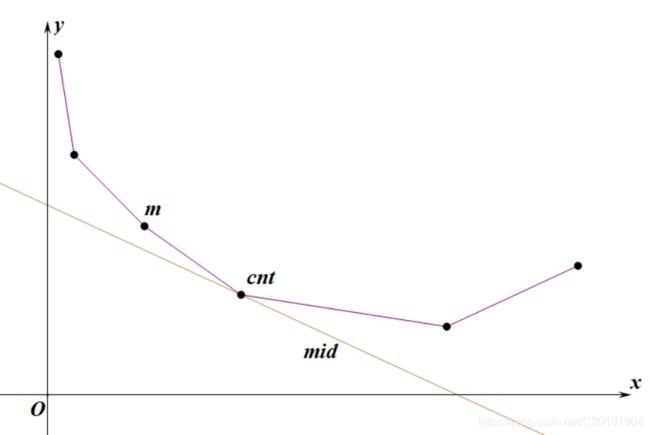
接下来并不是直接讨论 c n t = m cnt=m cnt=m。
我们来看一种必然会发生的情况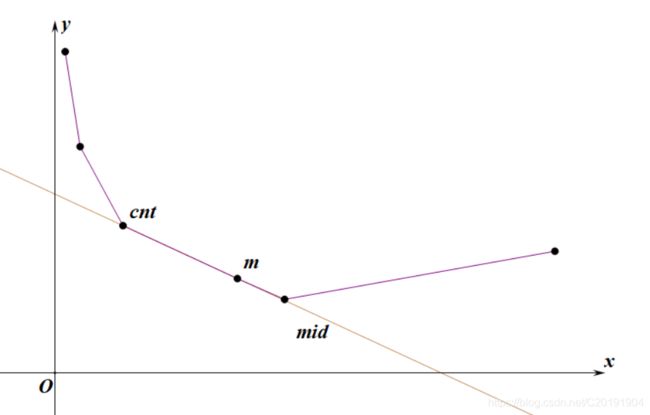
那么这时反映 m i d mid mid的点就是 c n t cnt cnt,可以感知的是我们永远不会二分到一个 C C C使得 c n t = m cnt=m cnt=m
但同样可以知道的是此时我们用 c n t cnt cnt和 m m m算出的答案都是一样的,这证明了我们在 ( L , R ] (L,R] (L,R]的设定下 c n t < m cnt
又因为我们的闭端点是 R R R,再结合以上的讨论,所以当 c n t = m cnt=m cnt=m时显然是该让 R = m i d R=mid R=mid。
下面会总结一个保证二分正确的模板。
二分模板
伪代码小王子。
int GetCnt() {
//在最优的情况下使得cnt最小
}
int BS() {
int l=RangeL-1,r=RangeR;//(l,r]
while(l+1<r) {
int mid=(l+r)/2;
C=mid;
if(GetCnt()<=m)
r=mid;
else l=mid;
}
C=r;
GetCnt();
return Ans;
}
代码
说不定你都快要把征途忘了吧
/*Wiz_HUA*/
#include总结
欢乐的时光总是那么短暂,写了一天(真的)也快要写完了。
最后再重申一下我对忘情水二分:用一个 C C C来限制决策数量以减少对数量的枚举,并在同一个 C C C中取到最优。让这个最优的方案满足题目要求(在数量上)。一般用来做恰好 m m m个的题目。
有关二分精度的问题,作者有空再填吧。
最最最最后,再次鸣谢:
强大的几何画板& KaTeX \KaTeX KATEX之神MiMiZhaner
附上他关于这个问题的讨论
沉迷讨论的LSK
T h a n k s Thanks Thanks F o r For For R e a d i n g ! Reading! Reading!