计算方法实验报告PC版 —王世儒、王金金
计算方法实验
—(14级计算机科学与技术2班)
实验仪器和环境:PC-机、codeblocks 10.05、MATLAB R2013a
编程语言:C、C++、MATLAB
实验一:编写程序求多项式的和
实验目的:
比较两种求和方法发计算复杂度,通过比较两种程序的运行时间来实现。
实验内容:
计算多项式:
方法一:一般算法,程序运行过程中,所算乘法次数为 ,由于所加项共(n+1)项,则加法次数为n,C语言代码实现如下:
#include
#include
#include
using namespace std;
double a[100005];
int main()
{
double second1,second2;
second1=(double)clock()/CLOCKS_PER_SEC;//clock()函数返回值本为毫秒,除以CLOCK_PER_SEC之后单位即变为秒
int n,x;
double mul,sum;
n=10000;//记得给n更换取值看所用时间的差别
x=1;//防止数据过大超范围,将x初始化为1
sum=0;
for(int i=0;i<=n;i++)
{
a[i]=1;//防止数据过大超范围,初始化为1
}
for(int i=0;i<=n;i++)
{
mul=1;
for(int j=0;j 方法二:秦九昭算法,已知递推公式为: ,u[n]即为所求结果,则整个过程中共进行了n次加法和n次乘法,C语言代码实现如下:
#include
#include
#include
#include
using namespace std;
double a[100005];
double u[100005];
int main()
{
double second1,second2;
second1=(double)clock()/CLOCKS_PER_SEC; //clock()函数返回值本为毫秒,除以CLOCK_PER_SEC之后单位即变为秒
int n,x;
n=100000;//记得给n更换取值看所用时间的差别
x=1;//防止数据过大超范围,将x初始化为1
memset(u,0,sizeof(u));
for(int i=0;i<=n;i++)
{
a[i]=1;
}
u[0]=a[n];
for(int i=1;i<=n;i++)
{
u[i]=u[i-1]*x+a[n-i];
}
cout<<"Pn(x)="< second2=(double)clock()/CLOCKS_PER_SEC; cout<<"second1="< cout<<"second2="< cout<<"用时为: "< return 0; } 当n=10000时,输出为: Pn(x)=10001 second1=0.001 second2=0.002 用时为: 0.001 当n=100000时,输出为: Pn(x)=100001 second1=0.001 second2=0.003 用时为: 0.002 经比较,秦九韶算法比普通的算法快得多,算法更加优化,运算时间更短,复杂度更小,且当n越大时,这种差距体现的更加明显,所以秦九韶算法是一种非常好的方法。 实验二:求解线性方程组的解 实验目的: 用雅克比迭代法和高斯-赛德尔迭代法解线性方程组Ax=b,式中A为非奇异实矩阵。在给定迭代初值的情况下,进行迭代,直到满足精度要求。 实验内容: 试分别用雅克比迭代法,高斯-赛德尔迭代法解线性方程组: 方法一:用雅克比迭代法求解线性方程组 MATLAB代码实现: yakebi.m文件函数实现:%函数名和文件名一致 %A=[5,1,-1,-2;2,8,1,3;1,-2,-4,-1;-1,3,2,7]; % b=[-2;-6;6;12];
function Y=yakebi(A,b)
if(any(diag(A))==0)
error('error,pause')
end
eps=input('误差限eps=');
N=input('迭代次数N=');
D=diag(diag(A));
B=inv(D)*(D-A);
f=inv(D)*b;
K=0;
x0=zeros(size(b));
while 1
x1=B*x0+f
K=K+1;
fprintf('第%d次迭代的近似解为',K)
disp(x1');
if norm(x1-x0,inf) fprintf('满足精度要求的解为\n') disp(x1'); break end if K>N fprintf('迭代超限') end x0=x1; end
Command Window 中实现:
>> A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-13 2 7];
>> b=[-2 -6 6 12]';
>> yakebi(A,b);
误差限eps=0.00001;
迭代次数N=50;
x1 =
-0.4000
-0.7500
-1.5000
1.7143
第1次迭代的近似解为 -0.4000 -0.7500 -1.5000 1.7143
x1 =
0.1357
-1.1054
-1.6536
2.4071
第2次迭代的近似解为 0.1357 -1.1054 -1.6536 2.4071
x1 =
0.4532
-1.4799
-1.5152
2.6798
第3次迭代的近似解为 0.4532 -1.4799 -1.5152 2.6798
x1 =
0.6649
-1.6788
-1.3167
2.8462
第4次迭代的近似解为 0.6649 -1.6788 -1.3167 2.8462
x1 =
0.8109
-1.8190
-1.2059
2.9050
第5次迭代的近似解为 0.8109 -1.8190 -1.2059 2.9050
x1 =
0.8846
-1.8914
-1.1140
2.9542
第6次迭代的近似解为 0.8846 -1.8914 -1.1140 2.9542
x1 =
0.9372
-1.9397
-1.0717
2.9695
第7次迭代的近似解为 0.9372 -1.9397 -1.0717 2.9695
x1 =
0.9614
-1.9639
-1.0382
2.9857
第8次迭代的近似解为 0.9614 -1.9639 -1.0382 2.9857
x1 =
0.9794
-1.9802
-1.0241
2.9899
第9次迭代的近似解为 0.9794 -1.9802 -1.0241 2.9899
x1 =
0.9872
-1.9881
-1.0125
2.9955
第10次迭代的近似解为 0.9872 -1.9881 -1.0125 2.9955
x1 =
0.9933
-1.9935
-1.0080
2.9966
第11次迭代的近似解为 0.9933 -1.9935 -1.0080 2.9966
x1 =
0.9958
-1.9961
-1.0041
2.9986
第12次迭代的近似解为 0.9958 -1.9961 -1.0041 2.9986
x1 =
0.9978
-1.9979
-1.0027
2.9989
第13次迭代的近似解为 0.9978 -1.9979 -1.0027 2.9989
x1 =
0.9986
-1.9987
-1.0013
2.9995
第14次迭代的近似解为 0.9986 -1.9987 -1.0013 2.9995
x1 =
0.9993
-1.9993
-1.0009
2.9996
第15次迭代的近似解为 0.9993 -1.9993 -1.0009 2.9996
x1 =
0.9995
-1.9996
-1.0004
2.9999
第16次迭代的近似解为 0.9995 -1.9996 -1.0004 2.9999
x1 =
0.9998
-1.9998
-1.0003
2.9999
第17次迭代的近似解为 0.9998 -1.9998 -1.0003 2.9999
x1 =
0.9998
-1.9999
-1.0001
3.0000
第18次迭代的近似解为 0.9998 -1.9999 -1.0001 3.0000
x1 =
0.9999
-1.9999
-1.0001
3.0000
第19次迭代的近似解为 0.9999 -1.9999 -1.0001 3.0000
x1 =
0.9999
-2.0000
-1.0000
3.0000
第20次迭代的近似解为 0.9999 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第21次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第22次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第23次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第24次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
满足精度要求的解为
1.0000 -2.0000 -1.0000 3.0000
经过计算结果可知雅克比迭代法需要经过迭代24次之后才能得到精确解。
方法二:用高斯-赛德尔迭代法求解线性方程组
MATLAB代码实现:
gaosi.m文件函数实现:%文件名和函数名一致
%A=[5,1,-1,-2;2,8,1,3;1,-2,-4,-1;-1,3,2,7];
% b=[-2;-6;6;12];
function Y=gaosi(A,b)
if(any(diag(A))==0)
error('error,pause')
end
eps=input('误差限eps=');
N=input('迭代次数N=');
D=diag(diag(A));
L=tril(A,-1)
%下三角
U=triu(A,1)
%上三角
B=(-inv(D+L))*U;
f=inv(D+L)*b;
K=0;
x0=zeros(size(b));
while 1
x1=B*x0+f
K=K+1;
fprintf('第%d次迭代的近似解为',K)
disp(x1');
if norm(x1-x0,inf) fprintf('满足精度要求的解为\n') disp(x1'); break end if K>N fprintf('迭代超限') end x0=x1; end
在Command Window里面,当输入系数矩阵A= 和矩阵b= 时,调用函数gaosi(A,b),之后显示为:
误差限eps=0.00001;
迭代次数N=50;
L =
0 0 0 0
2 0 0 0
1 -2 0 0
-1 3 2 0
U =
0 1 -1 -2
0 0 1 3
0 0 0 -1
0 0 0 0
x1 =
-0.4000
-0.6500
-1.2750
2.3000
第1次迭代的近似解为 -0.4000 -0.6500 -1.2750 2.3000
x1 =
0.3950
-1.5519
-1.2003
2.7787
第2次迭代的近似解为 0.3950 -1.5519 -1.2003 2.7787
x1 =
0.7818
-1.8374
-1.0805
2.9222
第3次迭代的近似解为 0.7818 -1.8374 -1.0805 2.9222
x1 =
0.9203
-1.9408
-1.0301
2.9718
第4次迭代的近似解为 0.9203 -1.9408 -1.0301 2.9718
x1 =
0.9709
-1.9784
-1.0110
2.9897
第5次迭代的近似解为 0.9709 -1.9784 -1.0110 2.9897
x1 =
0.9894
-1.9921
-1.0040
2.9963
第6次迭代的近似解为 0.9894 -1.9921 -1.0040 2.9963
x1 =
0.9961
-1.9971
-1.0015
2.9986
第7次迭代的近似解为 0.9961 -1.9971 -1.0015 2.9986
x1 =
0.9986
-1.9989
-1.0005
2.9995
第8次迭代的近似解为 0.9986 -1.9989 -1.0005 2.9995
x1 =
0.9995
-1.9996
-1.0002
2.9998
第9次迭代的近似解为 0.9995 -1.9996 -1.0002 2.9998
x1 =
0.9998
-1.9999
-1.0001
2.9999
第10次迭代的近似解为 0.9998 -1.9999 -1.0001 2.9999
x1 =
0.9999
-1.9999
-1.0000
3.0000
第11次迭代的近似解为 0.9999 -1.9999 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第12次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第13次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
x1 =
1.0000
-2.0000
-1.0000
3.0000
第14次迭代的近似解为 1.0000 -2.0000 -1.0000 3.0000
满足精度要求的解为
1.0000 -2.0000 -1.0000 3.0000
由计算结果可知,高斯赛德尔迭代法需要迭代14次才能计算出满足精度要求的解。
实验三:迭代法求解方程的根
实验目的:
用不同方法求任意实函数方程f(x)=0在自变量区间[a,b]内或某一点附近的实根,并比较方法的优劣性。通过迭代次数和所用时间进行比较。
实验内容:
用4种迭代法求解方程 +x-4=0的根。
方程可改写为:x= ㏑(4-x) ,即x=f(x)的形式,此时f(x)收敛,则得到普通迭代公式:
= ㏑(4- ) ,n=0,1,2,3,4,…
方法一:用一般迭代法和埃特金加速算法C语言实现求解方程的根,C++代码实现如下:
#include
#include
#include
#include
using namespace std;
double x[1000];
double e,eqs;
double xx[1000];
double ffi(double w)
{
return 0.5*log(4-w);
}
void fun()
{
int i;
for(i=1; ; i++)
{
x[i]=0.5*log(4-x[i-1]);
e=fabs(x[i]-x[i-1]);
if(e break; } printf("普通迭代法所求方程满足精度的根为:%.5lf,迭代次数为:%d\n",x[i],i); } void Aitken() { int i; for(i=1; ; i++) { xx[i]=ffi(x[i-1]); xx[i+1]=ffi(xx[i]); x[i]=1.0*(x[i-1]*xx[i+1]-xx[i]*xx[i])/(x[i-1]-2*xx[i]+xx[i+1]); e=fabs(x[i]-x[i-1]); if(e break; } printf("Aitken迭代法所求方程满足精度的根为:%.5lf,迭代次数为:%d\n",x[i],i); } int main() { memset(x,0,sizeof(x)); x[0]=1.0; eqs=0.00001; fun(); Aitken(); return 0; } 结果讨论及分析: 结果输出显示为: 普通迭代法求解得根为:0.61036,迭代次数为:5 Aitken迭代法所求得根为:0.61036,迭代次数为:3 方法二:牛顿法。由于要实现任意一个收敛函数的迭代解法,必须要用到求解方程的一阶导数,则用C或者C++语言实现起来有难度,则选用MATLAB语言来实现,特别注意函数在传递参数的过程中的传递方法的实现。 牛顿法公式: .m文件中所用函数实现:
function Y=nd(f0)
syms x;
f1(x)=f0;
eps=input('误差限eps=');
N=input('迭代次数N=');
K=0;
x0=1;
while 1
f2(x)=diff(f1(x));
x1=double(x0-f1(x0)/f2(x0));
K=K+1;
fprintf('第%d次迭代的近似解为\n',K)
disp(x1');
if abs(x1-x0) fprintf('满足精度要求的解为\n') disp(x1'); break end if K>N fprintf('迭代超限') end x0=x1; end
Command Window中操作实现为:
>> syms x;
>> f(x)=exp(2*x)+x-4;
>> nd(f(x));
误差限eps=0.00001;
迭代次数N=50;
第1次迭代的近似解为
0.7218
第2次迭代的近似解为
0.6207
第3次迭代的近似解为
0.6105
第4次迭代的近似解为
0.6104
第5次迭代的近似解为
0.6104
满足精度要求的解为
0.6104
方法三:弦解法
C++代码实现:
#include
#include
#include
#include
using namespace std;
double a[1010];
double f(double x)
{
returnexp(2*x)+x-4;
}
int main()
{
memset(a,0,sizeof(a));
inti;
intflag=0;
a[0]=0.5;
a[1]=1.0;
doublee=100.0;
for(i=2;i<=50;i++)
{
a[i]=a[i-1]-(a[i-1]-a[i-2])*f(a[i-1])/(f(a[i-1])-f(a[i-2]));
e=fabs(a[i]-a[i-1]);
if(e<=0.00001)
{
flag=1;
break;
}
}
if(flag==1)
printf("满足精度的近似解为: %.5lf, 迭代次数为: %d\n",a[i],i);
else
printf("迭代超限\n");
return0;
}
运行结果为:
满足精度的近似解为: 0.61036, 迭代次数为: 6
小结:由于C语言和C++语言不能提供强大的求导函数,所以用C实现的普通的方法和艾特金加速算法还有弦解法都只是针对该题目中该特定的方程,而MATLAB提供强大的数学计算,所以可以实现对任意一个函数的牛顿法求解。
特别注意:函数作为参数时,参数的传递。
实验四:用最小二乘法拟合多项式曲线
实验目的:
用最小二乘法,在已知函数在点 处的函数值 的情况下,求拟合多项式并画出拟合曲线。
实验内容:
题目:通过实验获得数据如下:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2 |
3 |
4 |
6 |
7 |
8 |
|
2 |
3 |
6 |
7 |
5 |
3 |
2 |
试用最小二乘法求解多项式曲线,使于此数据组相拟合。
MATLAB代码实现:
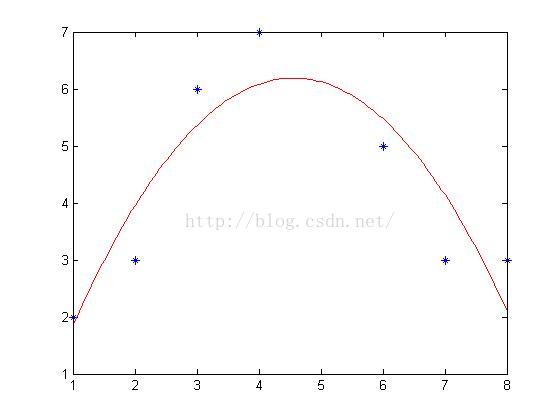
方法一:二次拟合
>> x=[1 2 3 4 6 7 8];
>> y=[2 3 6 7 5 3 2];
>> a=polyfit(x,y,2) %二次拟合
a =
-0.3864 3.4318 -1.3182 %多项式系数,按降幂排列,特别注意,该语句不能加分号,要让其直接显示出多项式的系数是多少,接下来要拿来使用。
>> x1=[1:0.05:8]; %以0.05为步长,从1到8,描点画线
>> y1=a(3)+a(2)*x1+a(1)*x1.^2; %y1为二次多项式的形式
>> plot(x,y,'*') %画X-Y轴
>> hold on %X-Y保持不变,继续作图
>> plot(x1,y1,'-r'); %用红色线条绘制拟合曲线
得到结果为如下图:
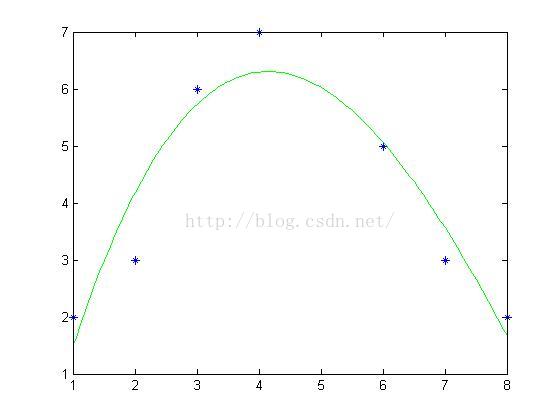
方法二:三次拟合
>> x=[1 2 3 4 6 7 8];
>> y=[2 3 6 7 5 3 2];
>> a=polyfit(x,y,3) %三次拟合曲线
a =
0.0251 -0.7200 4.6787 -2.5000 %多项式系数,按降幂排列
>> x1=[1:0.05:8];
>>y1=a(4)+a(3)*x1+a(2)*x1.^2+a(1)*x1.^3;
>> plot(x,y,'*')
>> hold on
>> plot(x1,y1,'-g'); %用绿色描绘三次拟合曲线
得到结果如下图所示:
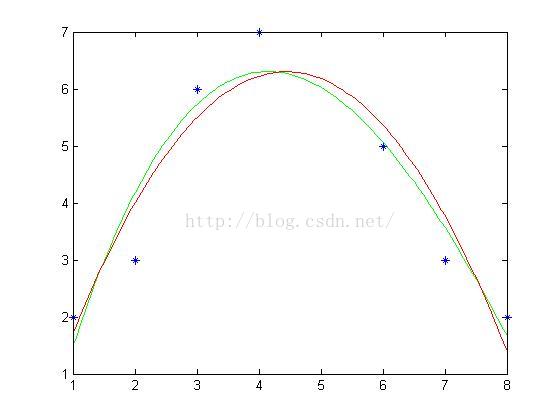
两种方法相比较得:
>> x=[1 2 3 4 6 7 8];
>> y=[2 3 6 7 5 3 2];
>> a=polyfit(x,y,3) %三次拟合曲线
a =
0.0251 -0.7200 4.6787 -2.5000 %多项式系数,按降幂排列
>> x1=[1:0.05:8];
>>y1=a(4)+a(3)*x1+a(2)*x1.^2+a(1)*x1.^3;
>> plot(x,y,'*')
>> hold on
>> plot(x1,y1,'-g'); %用绿色描绘三次拟合曲线
>> hold on %保持原状不变,继续画图
>> a=polyfit(x,y,2) %二次拟合曲线
a =
-0.3864 3.4318 -1.3182
>> x1=[1:0.05:8];
>> y1=a(3)+a(2)*x1+a(1)*x1.^2;
>> plot(x1,y1,'-r'); %把二次拟合曲线用红色线条描绘出来
得到结果如下图:
由上图可知,针对此问题,用二次拟合或者三次拟合所得到的图线相差不多,则两种方法都可以采用。
实验五:用数值积分的方法求解定积分
实验目的:
掌握梯形公式、新甫生公式和复化梯形公式、复化新甫生公式求解定积分并计算其精度。
实验内容:
㈠ 将积分区间等分为八等份,分别用梯形公式和新甫生公式计算定积分 的近似值。(MATLAB代码实现)
一、梯形公式:
function y=tixing(f1,a,b)
f(x)=f1; syms x;
s=double((f(a)+f(b))*(b-a)/2);
fprintf('梯形公式所求解为:\n');
disp(s);
Command Window 操作实现:
>> syms x;
>> f(x)=sqrt(1+x*x);
>> tixing(f(x),0,1)
梯形公式所求解为:
1.2071
二、复化梯形公式:
function y=fuhuatixing(f1)
syms x;
f(x)=f1;
a=input('积分下限a= ');
b=input('积分上限b= ');
n=input('等分次数n= ');
s=0;
k=0;
x0=a;
h=double((b-a)/n);
while 1
s=double(s+(f(x0)+f(double(x0+h)))/2);
fprintf('第%d次计算的结果为:\n',k);
disp(s);
k=k+1;
x0=x0+h;
if k>n-1
break;
end
end
%disp(s);
s=double(s*h);
fprintf('满足精度要求的解为:\n');
disp(s);
Command Window中操作为:
>> fuhuatixing(f(x))
积分下限a= 0;
积分上限b= 1;
等分次数n= 8;
第0次计算的结果为:
1.0039
第1次计算的结果为:
2.0232
第2次计算的结果为:
3.0726
第3次计算的结果为:
4.1656
第4次计算的结果为:
5.3142
第5次计算的结果为:
6.5288
第6次计算的结果为:
7.8182
第7次计算的结果为:
9.1897
满足精度要求的解为:
1.1487
三、复化辛甫生公式:
function y=simpson(f1)
syms x;
f(x)=f1;
a=input('积分下限a= ');
b=input('积分上限b= ');
n=input('等分次数n= ');
k1=0;
k2=0;
x0=a;
h=double(2*(b-a)/n);
%disp(h);
s=double(f(a)+f(b));
%disp(s);
s1=0;
s2=0;
x1=x0;
while 1
s1=s1+double(f(x0+h/2));
x0=x0+h;
k1=k1+1;
if k1>n/2-1
break;
end
end
while 1
s2=s2+double(f(x1+h));
x1=x1+h;
k2=k2+1;
if k2>=n/2-1
break;
end
end
%w=double(s+s1+s2);
%disp(w);
s=double(double(s+4*s1+2*s2)*h/6);
fprintf('复化辛甫生公式所求得解为:\n');
disp(s);
Command Window中操作为:
>> simpson(f(x))
积分下限a= 0;
积分上限b= 1;
等分次数n= 8;
复化辛甫生公式所求得解为:
1.1478
由上述两种复化的方法可知此两种方法都可以求得较为精确的解,但是哪种方法更好由于精度限制不能得到考量。
㈡ 通过用数值积分的方法求解计算已知圆的面积并判断复发梯形公式和复化新甫生公式的精度。
问题:已知圆心为(1,1),半径为1的圆的面积为 ,通过数值积分的方法,有
方法一、复化梯形公式:
>> syms x;
>> f1(x)=1+sqrt(1-(x-1)*(x-1));
>> fuhuatixing(f1(x))
积分下限a= 0;
积分上限b= 2;
等分次数n= 8;
第0次计算的结果为:
1.3307
第1次计算的结果为:
3.0945
第2次计算的结果为:
5.0116
第3次计算的结果为:
6.9957
第4次计算的结果为:
8.9798
第5次计算的结果为:
10.8970
第6次计算的结果为:
12.6607
第7次计算的结果为:
13.9914
满足精度要求的解为:
3.4979
>> s1=3.4979;
>> f2(x)=1-sqrt(1-(x-1)*(x-1));
>> fuhuatixing(f2(x));
积分下限a= 0;
积分上限b= 2;
等分次数n= 8;
第0次计算的结果为:
0.6693
第1次计算的结果为:
0.9055
第2次计算的结果为:
0.9884
第3次计算的结果为:
1.0043
第4次计算的结果为:
1.0202
第5次计算的结果为:
1.1030
第6次计算的结果为:
1.3393
第7次计算的结果为:
2.0086
满足精度要求的解为:
0.5021
>> s2=0.5021;
>> s=s1-s2
s =
2.9958
方法二、复化新甫生公式:
>> syms x;
>> f1(x)=1+sqrt(1-(x-1)*(x-1));
>> f2(x)=1-sqrt(1-(x-1)*(x-1));
>> simpson(f1(x));
积分下限a= 0;
积分上限b= 2;
等分次数n= 8;
复化辛甫生公式所求得解为:
3.5418
>> simpson(f2(x));
积分下限a= 0;
积分上限b= 2;
等分次数n= 8;
复化辛甫生公式所求得解为:
0.4582
>> s1=3.5418-0.4582
s1 =
3.0836
由上述比较可知,复化新甫生公式比复化梯形公式更加精确。