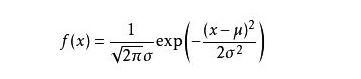机器学习数学基础总结（不断更新）

一、高数

1.1 

 

二、线代

2.1 

 

三、概率论

3.1 独立同分布 iid

        独立同分布independent and identically distributed (i.i.d.)  在西瓜书中解释是：输入空间中的所有样本服从一个隐含未知的分布，训练数据所有样本都是独立地从这个分布上采样而得。独立：每次抽样之间没有关系，不会相互影响；同分布：每次抽样，样本服从同一个分布；独立同分布：i,i,d，每次抽样之间独立而且同分布。

        独立同分布在机器学习中就是假设训练数据和测试数据是满足相同分布的，它是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。

        机器学习并不总要求独立同分布，在不少问题中要求样本数据采样自同一个分布是因为希望用训练数据集得到的模型可以合理的用于测试数据集，使用独立同分布假设能够解释得通。目前一些机器学习内容已经不再囿于独立同分布假设下，一些问题会假设样本没有同分布。

3.2 最大似然估计 MLE

        极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

        我们这样想，一当模型满足某个分布，它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下：

        通过极大似然估计，得到模型中参数μ和σ的值，那么这个模型的均值和方差（σ^2）以及其它所有的信息我们就都知道了。极大似然估计中采样需满足一个重要的假设，就是所有的采样都是独立同分布的。

3.3 概率分布函数和概率密度函数

        如果随机变量的值都可以逐个列举出来，例如，企业个数，职工人数，设备台数等则为离散型随机变量。如果随机变量X的取值无法逐个列举，例如，生产零件的规格尺寸，人体测量的身高，体重，胸围等则为连续型随机变量。        

研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！
所有概念，包括概率密度，概率分布，概率函数，都是在描述概率！

3.3.1 离散型随机变量的概率函数，概率分布和分布函数

        概率函数，就是用函数的形式来表达概率。概率函数一次只能表示一个取值的概率。比如P（X=1）=1/6,这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。

        概率分布，顾名思义就是概率的分布，这个概率分布还是讲概率的。我认为在理解这个概念时，关键不在于“概率”两个字，而在于“分布”这两个字。

        在很多教材中，这样的列表都被叫做离散型随机变量的“概率分布”。其实严格来说，它应该叫“离散型随机变量的值分布和值的概率分布列表”，这个名字虽然比“概率分布”长了点，但是肯定好理解了很多。因为这个列表，上面是值，下面是这个取值相应取到的概率，而且这个列表把所有可能出现的情况全部都列出来了！

        分布函数，全称叫做概率分布函数，下图中的分布律，这里的分布律明明就是我们刚刚讲的“概率函数”，完全就是一个东西。但是我知道很多教材就是叫分布律的。

        概率分布函数就是把概率函数累加。图上的公式，其中的F(x)就代表概率分布函数啦。这个符号的右边是一个长的很像概率函数的公式，但是其中的等号变成了小于等于号的公式。你再往右看看，这是一个一个的概率函数的累加！所以它又叫累积概率函数！概率函数和概率分布函数就像是一个硬币的两面，它们都只是描述概率的不同手段！

3.3.2 连续型随机变量的概率函数和分布函数

        连续型随机变量的“概率函数”换了一个名字，叫做“概率密度函数”。在陈希孺老师所著的《概率论与数理统计》这本书中，

        看看下面的这个公式：

        概率密度函数用数学公式表示就是一个定积分的函数，定积分在数学中是用来求面积的，而在这里，你就把概率表示为面积即可！

        左边是F(x)连续型随机变量分布函数画出的图形，右边是f(x)连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。两张图一对比，你就会发现，如果用右图中的面积来表示概率，利用图形就能很清楚的看出，哪些取值的概率更大！所以，我们在表示连续型随机变量的概率时，用f(x)概率密度函数来表示，是非常好的！

        概率密度函数在某一点的值的意义：某点的 概率密度函数 即为 概率在该点的变化率(或导数)。很容易误以为该点概率密度值 为 概率值.

3.4 常见分布函数