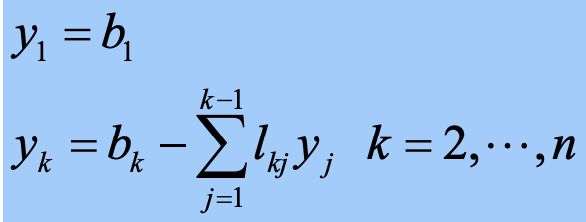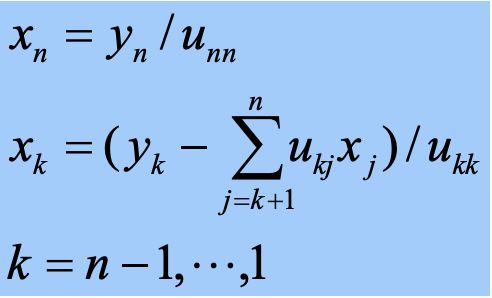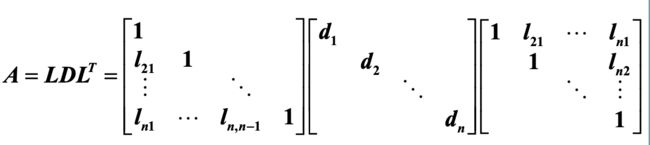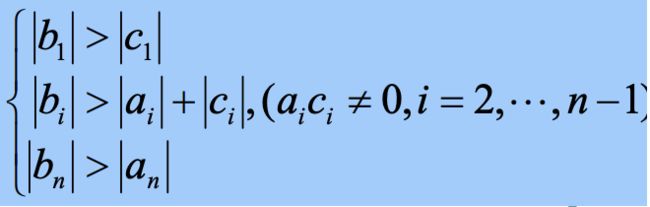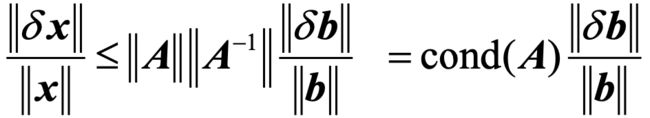线性和非线性方程数值解法_数值分析计算方法
传送门:
线性和非线性方程数值解法_数值分析计算方法
插值与逼近_数值分析计算方法
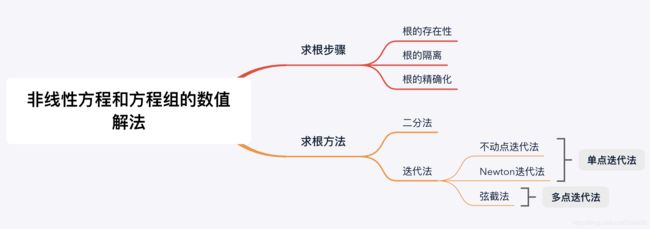
0 绪论
1 非线性方程数值解法
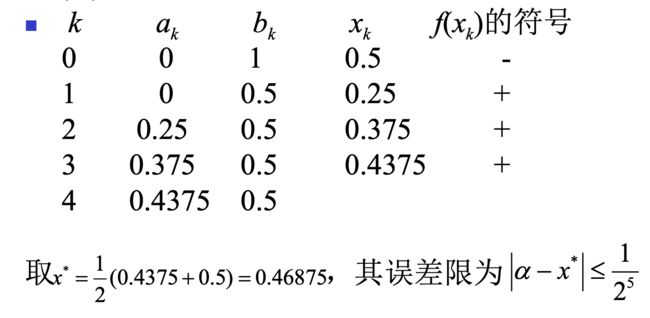
1.1 二分法
使用的条件
- 区间首尾异号
- 区间内连续
- 仅有一个根
步骤
先判断是否满足使用的条件,再使用
误差限的计算
1.2 迭代法
单点迭代法
将 f ( x ) = 0 f(x)=0 f(x)=0 改写成 x = ϕ ( x ) x=\phi(x) x=ϕ(x),
建立迭代公式 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk),
在根附近任取一点 x 0 x_0 x0,若得到的序列收敛于 α \alpha α且 ϕ ( x ) \phi(x) ϕ(x)连续
多点迭代法
x k + 1 = ϕ ( x k − n + 1 , . . . , x k − 2 , x k − 1 , x k ) x_{k+1}=\phi(x_{k-n+1}, ..., x_{k-2}, x_{k-1}, x_k) xk+1=ϕ(xk−n+1,...,xk−2,xk−1,xk)
迭代法的收敛性
全局收敛性:设 α \alpha α为 f ( x ) = 0 f(x)=0 f(x)=0的根,如果 ∀ x 0 ∈ [ a , b ] \forall x_0 \in [a, b] ∀x0∈[a,b] ,由迭代法产生的序列都收敛于根 α \alpha α, 则称该迭代法是全局收敛的;
局部收敛性:设方程 x = ϕ ( x ) x=\phi(x) x=ϕ(x)有根 α α α, 如果存在 α α α的某个邻域 Δ : ∣ x − α ∣ < δ \Delta: |x-\alpha| < \delta Δ:∣x−α∣<δ,对任意初值 x 0 ∈ Δ x_0 \in \Delta x0∈Δ,迭代过程所产生的序列均收敛于根 α α α,则称该迭代法是局部收敛的。
迭代过程的收敛速度
D e f . Def. Def. 记 e k = α − x k e_k=\alpha-x_k ek=α−xk,若 lim k → ∞ ∣ e k + 1 ∣ ∣ e k ∣ p = C ≠ 0 \displaystyle \lim_{k \to \infty}\frac{|e_{k+1}|}{|e_k|^p}=C\neq0 k→∞lim∣ek∣p∣ek+1∣=C=0,则称迭代过程是p阶收敛的;
特别地,当p=1时,称为线性收敛;
当p>1时,称为超线性收敛,
当p=2时,称为平方收敛.
迭代过程的效率指数
D e f . Def. Def. E I = p 1 θ EI=p^{1 \over \theta} EI=pθ1
为效率指数. 其中 p p p表示迭代的收敛阶, θ \theta θ表示每步迭代的计算量.
E I EI EI越大,计算效率越高.
1.2.1 不动点迭代法
T h 1.1 Th1.1 Th1.1 设 ϕ ( x ) \phi(x) ϕ(x)满足:
1)当 x ∈ [ a , b ] x\in[a, b] x∈[a,b]时, ϕ ( x ) ∈ [ a , b ] \phi(x)\in[a, b] ϕ(x)∈[a,b];
2) ∀ x 1 , x 2 ∈ [ a , b ] \forall x_1, x_2 \in [a, b] ∀x1,x2∈[a,b],有 ∣ ϕ ( x 1 ) − ϕ ( x 2 ) ∣ ≤ L ∣ x 1 − x 2 ∣ , L < 1 |\phi(x_1)-\phi(x_2)| \leq L|x_1-x_2|,L<1 ∣ϕ(x1)−ϕ(x2)∣≤L∣x1−x2∣,L<1,
则对任意初值 x 0 ∈ [ a , b ] x_0\in[a,b] x0∈[a,b],迭代过程 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk)收敛于 x = ϕ ( x ) x=\phi(x) x=ϕ(x)在 [ a , b ] [a, b] [a,b]上的唯一根 ,且有误差估计式: ∣ α − x k ∣ ≤ L 1 − L ∣ x k − x k − 1 ∣ |\alpha-x_k|\leq \frac L {1-L}|x_k-x_{k-1}| ∣α−xk∣≤1−LL∣xk−xk−1∣ ∣ α − x k ∣ ≤ L k 1 − L ∣ x 1 − x 0 ∣ |\alpha-x_k|\leq \frac {L^k} {1-L}|x_1-x_0| ∣α−xk∣≤1−LLk∣x1−x0∣
T h 1.2 Th1.2 Th1.2 设 ϕ ( x ) \phi(x) ϕ(x)在 [ a , b ] [a,b] [a,b]上具有一阶导数,且
1)当 x ∈ [ a , b ] x\in [a,b] x∈[a,b]时,有 ϕ ( x ) ∈ [ a , b ] \phi(x)\in[a,b] ϕ(x)∈[a,b];
2) ∀ x ∈ [ a , b ] \forall x \in [a,b] ∀x∈[a,b],有 ∣ ϕ ′ ( x ) ∣ ≤ L < 1 |\phi'(x)| \leq L < 1 ∣ϕ′(x)∣≤L<1,
则对任意初值 x 0 ∈ [ a , b ] x_0\in[a,b] x0∈[a,b],迭代过程 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk)收敛于 x = ϕ ( x ) x=\phi(x) x=ϕ(x)在 [ a , b ] [a, b] [a,b]上的唯一根。
T h 1.3 Th1.3 Th1.3 若 ϕ ( x ) \phi(x) ϕ(x)在方程 x = ϕ ( x ) x=\phi(x) x=ϕ(x)的根 α \alpha α的邻域内有一阶连续的导数,且 ∣ ϕ ′ ( x ) ∣ < 1 |\phi'(x)| < 1 ∣ϕ′(x)∣<1,则迭代过程 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk)具有局部收敛性。
T h 1.4 Th1.4 Th1.4 若 ϕ ( x ) \phi(x) ϕ(x)在方程 x = ϕ ( x ) x=\phi(x) x=ϕ(x)的根 α \alpha α的邻域内有充分阶连续的导数,则迭代过程 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk)在 α \alpha α的邻域是 p p p阶收敛的充要条件是 ϕ ( j ) ( α ) = 0 , j = 1 , 2 , . . . , p − 1 \phi^{(j)}(\alpha)=0, \quad j=1,2,...,p-1 ϕ(j)(α)=0,j=1,2,...,p−1 ϕ ( p ) ( α ) ≠ 0 \phi^{(p)}(\alpha) \neq 0 ϕ(p)(α)=0
1.2.2 牛顿迭代法
设有方程 f ( x ) = 0 f(x)=0 f(x)=0,在 f ( x ) = 0 f(x)=0 f(x)=0的根 α α α附近任取一点 x 0 x_0 x0作为初始近似根,由迭代公式 x k + 1 = x k − f ( x k ) f ′ ( x k ) ( k = 0 , 1 , 2... ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} \quad (k=0,1,2...) xk+1=xk−f′(xk)f(xk)(k=0,1,2...)逐次逼近方程 f ( x ) = 0 f(x)=0 f(x)=0的根 α α α,这种求根算法称为Newton法(切线法)。
局部收敛性:
T h Th Th Newton法的迭代函数是 ϕ ( x ) = x − f ( x ) f ′ ( x ) \phi(x)=x-\frac{f(x)}{f'(x)} ϕ(x)=x−f′(x)f(x),
若 α \alpha α是 f ( x ) = 0 f(x)=0 f(x)=0的一个单根,则在根α附近Newton法是局部二阶收敛的,即 p = 2 p=2 p=2;
若 α \alpha α是 f ( x ) = 0 f(x)=0 f(x)=0的一个重根,则在根α附近Newton法是局部线性收敛的,即 p = 1 p=1 p=1。
全局收敛性:
T h 1.5 Th1.5 Th1.5 设 f ( x ) f(x) f(x)在有根区间 [ a , b ] [a, b] [a,b]上二阶导数存在,且满足:
1) f ( a ) f ( b ) < 0 f(a)f(b)<0 f(a)f(b)<0;
2) f ′ ( x ) ≠ 0 , x ∈ [ a , b ] f'(x) \neq 0,\quad x \in [a,b] f′(x)=0,x∈[a,b];
3) f ′ ′ ( x ) f''(x) f′′(x)不变号 , x ∈ [ a , b ] ,\quad x \in [a,b] ,x∈[a,b];
4)初值 x 0 ∈ [ a , b ] x_0 \in [a,b] x0∈[a,b]且使 f ′ ′ ( x 0 ) f ( x 0 ) > 0 f''(x_0)f(x_0)>0 f′′(x0)f(x0)>0,
则 Newton迭代法收敛于 f ( x ) = 0 f(x)=0 f(x)=0在 [ a , b ] [a, b] [a,b]内的唯一根。
简化Newton迭代法
x k + 1 = x k − f ( x k ) C , k = 0 , 1 , 2 , . . . x_{k+1} = x_k - \frac{f(x_k)}{C} ,\quad k=0,1,2,... xk+1=xk−Cf(xk),k=0,1,2,...一般地,取 C = f ′ ( x 0 ) C=f'(x_0) C=f′(x0). 若 ∣ ϕ ′ ( x ) ∣ = ∣ 1 − f ′ ( x ) C ∣ < 1 |\phi'(x)|=|1-\frac{f'(x)}{C}|<1 ∣ϕ′(x)∣=∣1−Cf′(x)∣<1,则是一阶收敛的.
Newton下山法
x k + 1 = x k − λ f ( x k ) f ′ ( x k ) ( 0 < λ ≤ 1 , k = 0 , 1 , 2... ) x_{k+1}=x_k-\lambda\frac{f(x_k)}{f'(x_k)} \quad (0<\lambda \leq1, k=0,1,2...) xk+1=xk−λf′(xk)f(xk)(0<λ≤1,k=0,1,2...)其中 λ \lambda λ为下山因子, λ \lambda λ的选取应该满足条件: ∣ f ( x k + 1 ∣ < ∣ f ( x k ) ∣ |f(x_{k+1}|<|f(x_k)| ∣f(xk+1∣<∣f(xk)∣,从而保证所得的序列是收敛的.
1.2.3 弦截法
由牛顿迭代法修改而来,用两点之间的弦截线代替切线,无需每次迭代都求导:
在方程 f ( x ) = 0 f(x)=0 f(x)=0的根 α α α附近任取两初始近似根 x 0 x_0 x0, x 1 x_1 x1,由迭代公式
x k + 1 = x k − x k − x k − 1 f ( x k ) − f ( x k − 1 ) f ( x k ) ( k = 0 , 1 , 2 , . . . ) x_{k+1}=x_k-\frac{x_k-x_{k-1}}{f(x_k)-f(x_{k-1})}f(x_k)\quad(k=0,1,2,...) xk+1=xk−f(xk)−f(xk−1)xk−xk−1f(xk)(k=0,1,2,...)逐次逼近 f ( x ) = 0 f(x)=0 f(x)=0的根 α α α,这种求根算法称为弦截法.
收敛阶 p = 1 + 5 2 p=\frac{1+\sqrt5}2 p=21+5,指数效率 E I = 1 + 5 2 EI=\frac{1+\sqrt5}2 EI=21+5
1.2.4 重根情形的迭代法
已知根的重数 r r r
将Newton法修正为 x k + 1 = x k − r f ( x k ) f ′ ( x k ) k = 0 , 1 , 2 , . . . x_{k+1}=x_k-r\frac{f(x_k)}{f'(x_k)}\quad k=0,1,2,... xk+1=xk−rf′(xk)f(xk)k=0,1,2,...它是求 r r r重根 α α α的二阶局部收敛格式.
[证明]
根的重数未知
将Newton法修正为 x k + 1 = x k − u ( x k ) u ′ ( x k ) k = 0 , 1 , 2 , . . . x_{k+1}=x_k-\frac{u(x_k)}{u'(x_k)}\quad k=0,1,2,... xk+1=xk−u′(xk)u(xk)k=0,1,2,...其中 u ( x ) = f ( x ) f ′ ( x ) u(x) = \frac{f(x)}{f'(x)} u(x)=f′(x)f(x)
f ( x ) = 0 f(x)=0 f(x)=0的 r r r重根就是 u ( x ) = 0 u(x)=0 u(x)=0单根,故它是求 f ( x ) = 0 f(x)=0 f(x)=0重根的二阶局部收敛格式.
[证明]
迭代加速收敛的方法
1.2.5 解非线性方程组
Newton迭代法
直观解释:每一次迭代,目标函数在局部可以近似表示成二次函数,然后以该二次函数的极值点来代替目标函数的极值点,不断重复直到收敛。
拟Newton迭代法
2 线性方程数值解法
线性方程组 A x = b \pmb{Ax}=\pmb{b} AxAxAx=bbb,这里只讨论系数矩阵为非奇异的线性方程组。
计算机上求解线性方程组的方法:
- 直接法:其基本思想是通过等价 变换将线性方程组化为结构简单、易于求解的形 式,从而求解;
- 迭代法:基本思想是用某种极限过程逐次逼近方程组的解的方法。它具有占有储存单元少、程序设计简单、原始系数矩阵在计算过程中不变的优点,但需考虑收敛性和收 敛速度问题。
2.1 基本知识
向量的范数
1-范数: ∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1 = \sum\limits_{i=1}^n|x_i| ∣∣x∣∣1=i=1∑n∣xi∣
2-范数: ∣ ∣ x ∣ ∣ 2 = ( ∑ i = 1 n x i 2 ) 1 2 ||x||_2 = (\sum\limits_{i=1}^nx_i^2)^{1 \over 2} ∣∣x∣∣2=(i=1∑nxi2)21
∞ \infty ∞-范数: ∣ ∣ x ∣ ∣ ∞ = max 1 ≤ i ≤ n ∣ x i ∣ ||x||_\infty = \max\limits_{1 \leq i \leq n}|x_i| ∣∣x∣∣∞=1≤i≤nmax∣xi∣
p p p-范数: ∣ ∣ x ∣ ∣ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p ||x||_p = (\sum\limits_{i=1}^n|x_i|^p)^{1 \over p} ∣∣x∣∣p=(i=1∑n∣xi∣p)p1
(范数连续性定理)设 f ( x ) = ∣ ∣ x ∣ ∣ f(x)=||x|| f(x)=∣∣x∣∣为 R n \pmb{R}^n RRRn上任一向量范数,则 f ( x ) f(x) f(x)是 x x x的连续函数。
(范数等价性定理)设 ∣ ∣ x ∣ ∣ s , ∣ ∣ x ∣ ∣ t ||x||_s,\ ||x||_t ∣∣x∣∣s, ∣∣x∣∣t为 R n \pmb{R}^n RRRn上任意两种向量范数,则存在常数 c 1 , c 2 > 0 c1,\ c2>0 c1, c2>0,使得 c 1 ∣ ∣ x ∣ ∣ s ≤ ∣ ∣ x ∣ ∣ t ≤ c 2 ∣ ∣ x ∣ ∣ s , ∀ x ∈ R n c_1||x||_s \leq ||x||_t \leq c_2||x||_s , \forall x \in \pmb{R}^n c1∣∣x∣∣s≤∣∣x∣∣t≤c2∣∣x∣∣s,∀x∈RRRn.
(定理)向量序列 x ( k ) {x^{(k)}} x(k)收敛于 x ∗ x^* x∗的充分且必要条件 ∣ ∣ x ( k ) − x ∗ ∣ ∣ → 0 , k → ∞ ||x^{(k)}-x^*||\to0, k\to\infty ∣∣x(k)−x∗∣∣→0,k→∞ ,其中 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣是任一向量范数.
矩阵的范数
…
∣ ∣ A ∣ ∣ F = ( ∑ i = 1 n ∑ j = 1 n a i j 2 ) 1 2 ||A||_F = (\sum\limits_{i=1}^n\sum\limits_{j=1}^na_{ij}^2)^{1 \over 2} ∣∣A∣∣F=(i=1∑nj=1∑naij2)21
对于给定向量范数 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣和矩阵范数 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣,如果对任何向量 x ∈ R n x\in \pmb{R}^n x∈RRRn (或 C n \pmb{C}^n CCCn)和 A ∈ R n ∗ n A\in \pmb{R}^{n*n} A∈RRRn∗n(或 C n ∗ n \pmb{C}^{n*n} CCCn∗n),都有不等式 ∣ ∣ A x ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ x ∣ ∣ ||Ax||\leq||A||\cdot||x|| ∣∣Ax∣∣≤∣∣A∣∣⋅∣∣x∣∣成立,则称所给的矩阵范数与向量范数是相容的。
1-范数(列和范数): ∣ ∣ A ∣ ∣ 1 = max 1 ≤ j ≤ n ∑ i = 1 n ∣ a i j ∣ ||A||_1 = \max\limits_{1\leq j \leq n}\sum\limits_{i=1}^n|a_{ij}| ∣∣A∣∣1=1≤j≤nmaxi=1∑n∣aij∣
2-范数(谱范数): ∣ ∣ A ∣ ∣ 2 = ρ ( A H A ) ||A||_2 = \sqrt{\rho(A^HA)} ∣∣A∣∣2=ρ(AHA), A H A^H AH是 A A A的共轭转置矩阵
∞ \infty ∞-范数(行和范数): ∣ ∣ A ∣ ∣ ∞ = max 1 ≤ i ≤ n ∑ j = 1 n ∣ a i j ∣ ||A||_\infty = \max\limits_{1\leq i \leq n}\sum\limits_{j=1}^n|a_{ij}| ∣∣A∣∣∞=1≤i≤nmaxj=1∑n∣aij∣
定义设n阶方阵A的特征值为 λ 1 , λ 2 , . . . , λ n \lambda_1,\ \lambda_2,\ ...\ ,\lambda_n λ1, λ2, ... ,λn,则称 ρ ( A ) = max 1 ≤ i ≤ n ∣ λ i ∣ \rho(A) = \max\limits_{1\leq i \leq n}|\lambda_i| ρ(A)=1≤i≤nmax∣λi∣为 A A A的谱半径。
对于任意从属范数 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣, ρ ( A ) ≤ ∣ ∣ A ∣ ∣ \rho(A) \leq ||A|| ρ(A)≤∣∣A∣∣;
但当 A A A是正规矩阵,即 A A H A A^H AAH = A H A A^H A AHA时, ρ ( A ) = ∣ ∣ A ∣ ∣ 2 \rho(A)=||A||_2 ρ(A)=∣∣A∣∣2;
显然若A为实对称矩阵,则 ρ ( A ) = ∣ ∣ A ∣ ∣ 2 \rho(A)=||A||_2 ρ(A)=∣∣A∣∣2;
矩阵范数也有相应向量范数三个定理(范数连续性、范数等价性、向量序列收敛的充要条件)结论。
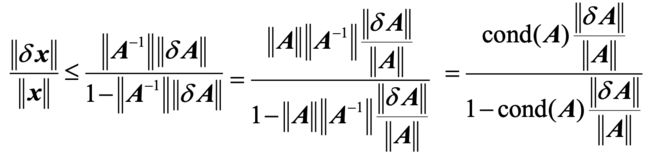
设 A A A为非奇异矩阵,称数 c o n d v ( A ) = ∣ ∣ A ∣ ∣ v ∣ ∣ A − 1 ∣ ∣ v cond_v(A) = ||A||_v ||A^{-1}||_v condv(A)=∣∣A∣∣v∣∣A−1∣∣v为矩阵 A A A的条件数.
c o n d v ( A ) = ∣ ∣ A ∣ ∣ v ∣ ∣ A − 1 ∣ ∣ v ≥ ∣ ∣ A A − 1 ∣ ∣ v = 1 cond_v(A) = ||A||_v ||A^{-1}||_v \geq ||AA^{-1}||_v = 1 condv(A)=∣∣A∣∣v∣∣A−1∣∣v≥∣∣AA−1∣∣v=1
2.2 直接法
2.2.1 Gauss消去法
但如果主元素的绝对值很小,用它除数,势必造成舍入误差的严重扩散,以致于方程组的解的精度受到严重影响,于是有:
选列主元的Gauss消去法
全选主元的Gauss消去法
ZJU的PPT
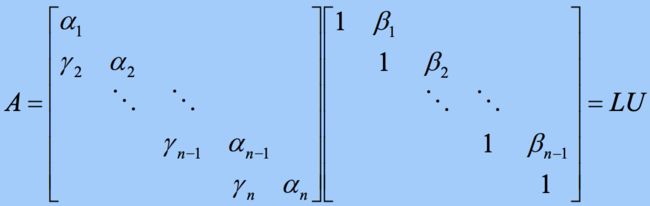
2.2.2 矩阵三角分解法
Doolittle分解法(直接三角分解法)
如果 A A A的所有顺序主子式均不为零,则 A A A可唯一分解为 A = L U A=LU A=LU,其中 L L L为单位下三角阵, U U U为上三角阵。
原方程组 A x = B Ax=B Ax=B,可改写为 L U x = B LUx = B LUx=B,令 y = U x y=Ux y=Ux可利用 L ( U x ) = L y = B L(Ux) = Ly= B L(Ux)=Ly=B求出 y y y,再由 y = U x y=Ux y=Ux求 x x x。
1)先求 L , U L, U L,U, O ( n 3 − n 3 ) O(\frac{n^3-n}3) O(3n3−n)
L L L从左往右逐列求, U U U从上往下逐行求
求出 U U U的前 k − 1 k-1 k−1行与 L L L的前 k − 1 k-1 k−1列后,第 k k k步中计算 U U U的第 k k k行、 L L L的第 k k k列元素的公式为:
2)由 L y = B Ly=B Ly=B求 y y y, O ( n 2 ) O(n^2) O(n2)
3)由 y = U x y=Ux y=Ux求 x x x, O ( n 2 ) O(n^2) O(n2)
Crout分解法
A = L ^ U ^ A=\hat L \hat U A=L^U^,其中 L ^ \hat L L^为下三角阵, U ^ \hat U U^为单位上三角阵。
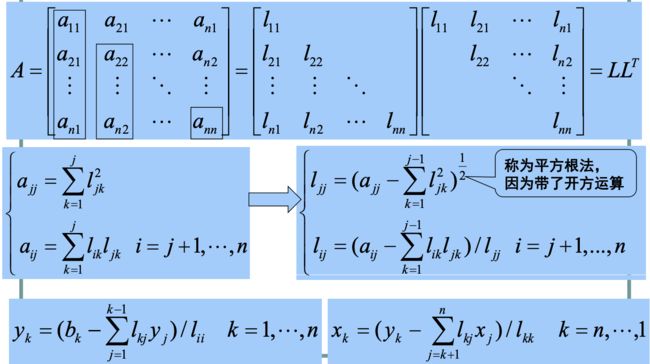
Cholesky分解法(对称正定矩阵方程组的平方根法)
若 A A A满足:
1)对称性, A T = A A^T = A AT=A
2)正定性, x T A x > 0 , ∀ x ∈ R n , x ≠ 0 x^TAx > 0, \forall x \in \textbf R^n, x ≠ 0 xTAx>0,∀x∈Rn,x=0
则 A A A可分解为 A = L L T A=LL^T A=LLT, L L L为非奇异下三角矩阵。
改进的 Cholesky 分解
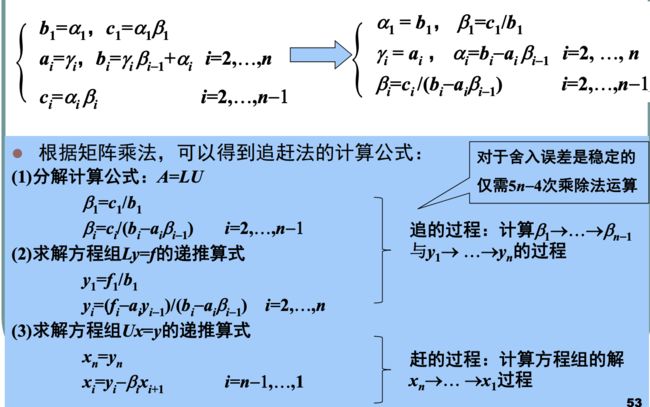
三对角方程组的追赶法
若
满足
则可以分解
于是可以计算
2.2.3 误差分析
线性代数方程组计算中得到近似计算结果的原因:
1)计算机的字长有限,不可避免地产生舍入误差;
2)初始数据有问题:由于系数矩阵 A A A和右端项 b b b元素带有某些观测误差,往往不是准确给出,或 A , b A,b A,b元素是计算结果,包含舍入误差。
方程组 A x = b Ax=b Ax=b的右端 b b b的扰动对解 x x x的影响
方程组 A x = b Ax=b Ax=b的系数阵 A A A的扰动对解 x x x的影响
2.3 迭代法
2.3.1 迭代法的收敛性
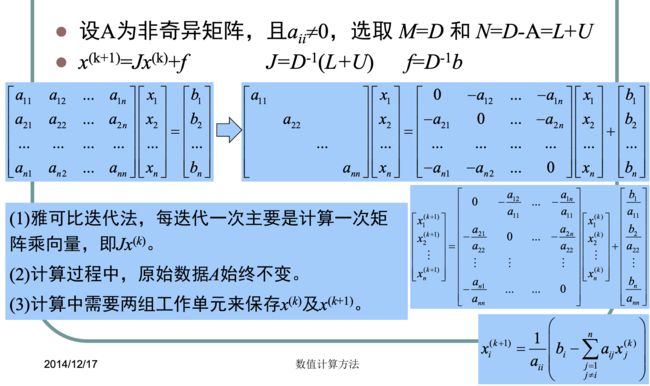
Th1)设 B ∈ K n ∗ n B \in \textbf K ^{n*n} B∈Kn∗n, lim k → ∞ B k \lim \limits_{k \to \infty}{B ^ k} k→∞limBk的充分必要条件是 ρ ( B ) < 1 \rho(B) < 1 ρ(B)<1
Th2)(迭代法的基本收敛定理)迭代过程 x k + 1 = B x k + g x^{k+1} = Bx^k+ g xk+1=Bxk+g 对于任意初始向量 x ( 0 ) x^{(0)} x(0)及右端向量 g g g均收敛的充分必要条件是迭代矩阵 B B B的谱半径 ρ ( B ) < 1 \rho(B)<1 ρ(B)<1, 并且 ρ ( B ) \rho(B) ρ(B)愈小,收敛速度愈快。
由此可知:迭代法的收敛性与收敛速度与迭代矩阵 B B B有关,而与右端向量 g g g和初始向量 x ( 0 ) x^{(0)} x(0)无关。
2.3.2 迭代法的误差估计
设 x ∗ x^* x∗为方程组 A x = b Ax=b Ax=b的精确解. 若迭代法 x k + 1 = B x k + g x^{k+1} = Bx^k+ g xk+1=Bxk+g 的迭代矩阵 B B B满足 ∣ ∣ B ∣ ∣ < 1 ||B||<1 ∣∣B∣∣<1,其中 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣是某种算子范数,则对于任意的初始向量 x ( 0 ) x^{(0)} x(0)与右端向量 g g g迭代法收敛,且有如下两个误差估计式:
2.3.3 基本迭代方法
2.3.4 Jacobi迭代法(同步迭代法)
2.3.5 高斯-赛德尔(Gauss-Seidel)迭代法(异步迭代法)
2.3.6 超松弛迭代法(SOR方法)
超松弛法收敛的必要条件为 0 < ω < 2 0<\omega<2 0<ω<2
2.3.7 某些特殊方程组迭代法的收敛性
Th.1 若线性方程组 A x = b Ax=b Ax=b的系数矩阵 A A A为对称正定阵,则Gauss-Seidel迭代法收敛.
Th.2 若线性方程组 A x = b Ax=b Ax=b的系数矩阵 A A A为对称正定阵,则当 0 < ω < 2 0<\omega<2 0<ω<2时, SOR方法收敛.
Def 称方阵 A = ( a i j ) n n A=(a_{ij})_{nn} A=(aij)nn为严格对角占优的,如果 ∑ j = 1 , j ≠ i n ∣ a i j ∣ < ∣ a i i ∣ ( i = 1 , 2 , . . . , n ) \sum \limits_{j=1,j≠i}^n |a_{ij}| < |a_{ii}|\quad(i = 1,2,...,n) j=1,j=i∑n∣aij∣<∣aii∣(i=1,2,...,n)或 ∑ j = 1 , j ≠ i n ∣ a i j ∣ < ∣ a j j ∣ ( j = 1 , 2 , . . . , n ) \sum \limits_{j=1,j≠i}^n |a_{ij}| < |a_{jj}|\quad(j = 1,2,...,n) j=1,j=i∑n∣aij∣<∣ajj∣(j=1,2,...,n)
Th.3 若线性方程组 A x = b Ax=b Ax=b的系数方阵 A = ( a i j ) n n A=(a_{ij})_{nn} A=(aij)nn是按行(或按列)严格对角占优的,则 Jacobi迭代法 和 Gauss-Seidel迭代法 都是收敛的。
Th.4 若线性方程组 A x = b Ax=b Ax=b的系数矩阵 A A A为严格对角占优矩阵,则当 0 < ω ≤ 1 0<\omega \leq 1 0<ω≤1时,SOR方法收敛。
Th.5 设 A A A是具有正对角线元素的对称矩阵,则解线性方程组 A x = b Ax=b Ax=b的Jacobi迭代法收敛的充分必要条件是 A A A和 2 D − A 2D-A 2D−A都为对称正定阵。
2.4 梯度法
ZJU的课件地址
任何组织或个人未经作者授权许可,均不得以任何方式或理由全文转载以及全文复制;
也不得修改、改编、盗链或制作镜像等。