基于Sklearn的多项式回归算法与Pipeline使用详解

基本思想：
将X^2与X理解为两个不同特征，所以平方项会让数据增加一个特征。
从[X^2,X,1]角度看，是一个线性方程
从[X,1]角度看，是一个非线性方程

一、多项式回归的由来

且看代码，比较两种线性回归方式的拟合效果

import numpy as np 
import matplotlib.pyplot as plt 
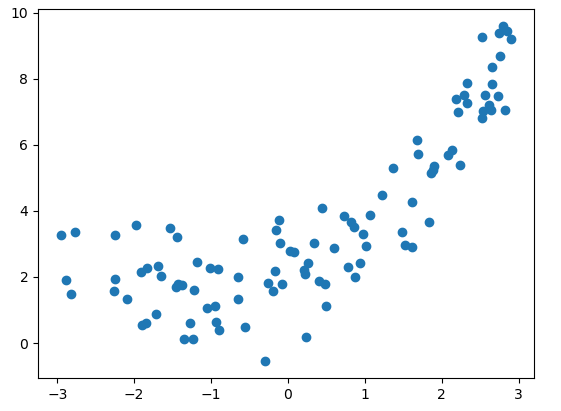
x = np.random.uniform(-3,3,size = 100)
#sklearn输入数据是矩阵类型，将x转换成二维矩阵
X = x.reshape(-1,1)  
#给方程增加点噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size = 100)
#绘制数据集分布的图
#plt.scatter(x,y)
#plt.show()
#图像见Figure1

Figure1

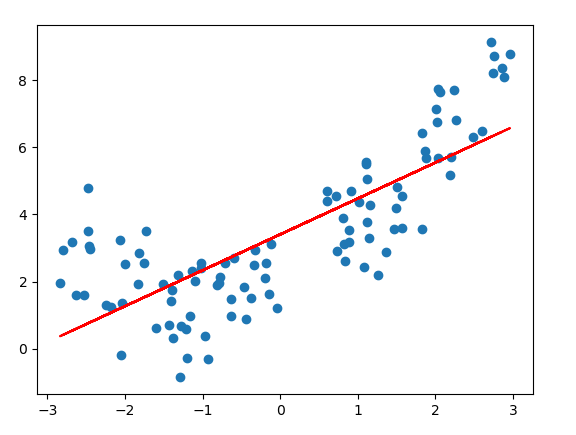
#Method1
#用线性回归拟合数据集:lin_reg
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
y_predict = lin_reg.predict(X)

plt.scatter(x,y)
plt.plot(x,y_predict,color = 'r')
plt.show()
#图像见Figure2

Figure2

#Method2
#从图像看，线性回归拟合得不够好
#解决：添加一个特征X2
X2 = np.hstack([X,X**2]) 
#新的数据集增加了一列
#用新的数据集进行线性回归拟合:lin_reg2
lin_reg2 = LinearRegression()
lin_reg2.fit(X2,y)
y_predict2 = lin_reg2.predict(X2)

plt.scatter(x,y)
plt.plot(x,y_predict2,color = 'r')
plt.show()
#图像见Figure3 
#Figure3的问题：x是没有顺序的

Figure3

#要生成平滑的曲线，需要对x进行排序
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color = 'r')
plt.show()
#图像见Figure4
#多项式回归采用线性回归的思路，对特征进行升维，解决了非线性问题

Figure4

二、Sklearn实现多项式回归

import numpy as np 
import matplotlib.pyplot as plt 
#生成虚拟数据集
x = np.random.uniform(-3,3,size = 100)
X = x.reshape(-1,1)  
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size = 100)

from sklearn.preprocessing import PolynomialFeatures
#degree :为数据添加几次幂
ploy = PolynomialFeatures(degree = 2)
ploy.fit(X)
X2 = ploy.transform(X)
#里面已经在第一列添加一列1了，所以不需要增加一列纯1的X0

from sklearn.linear_model import LinearRegression
lin_reg2 = LinearRegression()
lin_reg2.fit(X2,y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color = 'r')
plt.show()
#结果同Figure4

PolynomialFeatures机制

三、基于sklearn-Pipeline的多项式回归

每次进行多项式回归需要重复三个步骤：

1. 多项式的特征

2. 数据的归一化

3. 线性回归

使用Pipeline可以将这三步合在一起，避免调用时的重复

——————————我是分割线^ _ ^ —————————————

构造Pipeline时，传入的是一个列表

列表中包含：实现多项式回归的每一个步骤对应的那个类

每一个步骤对应的那个类：以元组的形式传入

每一个元组包含：

1. 表示步骤名称的字符串
2. 需要实例化的操作

from sklearn.pipeline import Pipeline
poly_reg = Pipeline([
	        ("poly",PolynomialFeatures(degree = 2)),
		  ("std_scaler",StandardScaler()),
		  ("lin_reg",LinearRegression())
	])

完整代码

import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.preprocessing import StandardScaler

x = np.random.uniform(-3,3,size = 100)
X = x.reshape(-1,1)  
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size = 100)

from sklearn.pipeline import Pipeline

poly_reg = Pipeline([
	        ("poly",PolynomialFeatures(degree = 2)),
		  ("std_scaler",StandardScaler()),
		  ("lin_reg",LinearRegression())
	])

poly_reg.fit(X,y)
#预测时使用Pipeline实例的predict
y_predict = poly_reg.predict(X)

转载于：
作者：郑可夫斯基
链接：http://www.imooc.com/article/286593
来源：慕课网