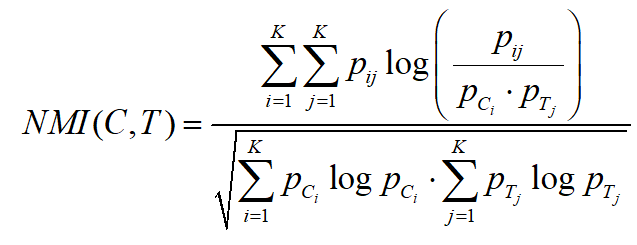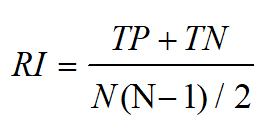MATLAB聚类有效性评价指标(外部)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
更多内容,请看标签:MATLAB、聚类
前提:数据的真实标签已知!
1. 归一化互信息(Normalized Mutual information)
定义
程序
function MIhat = nmi(A, B)
%NMI Normalized mutual information
% A, B: 1*N;
if length(A) ~= length(B)
error('length( A ) must == length( B)');
end
N = length(A);
A_id = unique(A);
K_A = length(A_id);
B_id = unique(B);
K_B = length(B_id);
% Mutual information
A_occur = double (repmat( A, K_A, 1) == repmat( A_id', 1, N ));
B_occur = double (repmat( B, K_B, 1) == repmat( B_id', 1, N ));
AB_occur = A_occur * B_occur';
P_A= sum(A_occur') / N;
P_B = sum(B_occur') / N;
P_AB = AB_occur / N;
MImatrix = P_AB .* log(P_AB ./(P_A' * P_B)+eps);
MI = sum(MImatrix(:));
% Entropies
H_A = -sum(P_A .* log(P_A + eps),2);
H_B= -sum(P_B .* log(P_B + eps),2);
%Normalized Mutual information
MIhat = MI / sqrt(H_A*H_B);
结果
>> A = [1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3];
>> B = [1 2 1 1 1 1 1 2 2 2 2 3 1 1 3 3 3];
>> MIhat = nmi(A, B)
MIhat =
0.3646
2. Rand统计量(Rand index)
定义
程序
function [AR,RI,MI,HI]=RandIndex(c1,c2)
%RANDINDEX - calculates Rand Indices to compare two partitions
% ARI=RANDINDEX(c1,c2), where c1,c2 are vectors listing the
% class membership, returns the "Hubert & Arabie adjusted Rand index".
% [AR,RI,MI,HI]=RANDINDEX(c1,c2) returns the adjusted Rand index,
% the unadjusted Rand index, "Mirkin's" index and "Hubert's" index.
if nargin < 2 || min(size(c1)) > 1 || min(size(c2)) > 1
error('RandIndex: Requires two vector arguments')
return
end
C=Contingency(c1,c2); %form contingency matrix
n=sum(sum(C));
nis=sum(sum(C,2).^2); %sum of squares of sums of rows
njs=sum(sum(C,1).^2); %sum of squares of sums of columns
t1=nchoosek(n,2); %total number of pairs of entities
t2=sum(sum(C.^2)); %sum over rows & columnns of nij^2
t3=.5*(nis+njs);
%Expected index (for adjustment)
nc=(n*(n^2+1)-(n+1)*nis-(n+1)*njs+2*(nis*njs)/n)/(2*(n-1));
A=t1+t2-t3; %no. agreements
D= -t2+t3; %no. disagreements
if t1==nc
AR=0; %avoid division by zero; if k=1, define Rand = 0
else
AR=(A-nc)/(t1-nc); %adjusted Rand - Hubert & Arabie 1985
end
RI=A/t1; %Rand 1971 %Probability of agreement
MI=D/t1; %Mirkin 1970 %p(disagreement)
HI=(A-D)/t1; %Hubert 1977 %p(agree)-p(disagree)
function Cont=Contingency(Mem1,Mem2)
if nargin < 2 || min(size(Mem1)) > 1 || min(size(Mem2)) > 1
error('Contingency: Requires two vector arguments')
return
end
Cont=zeros(max(Mem1),max(Mem2));
for i = 1:length(Mem1)
Cont(Mem1(i),Mem2(i))=Cont(Mem1(i),Mem2(i))+1;
end
程序中包含了四种聚类度量方法:Adjusted Rand index、Rand index、Mirkin index、Hubert index。
结果
>> A = [1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3];
>> B = [1 2 1 1 1 1 1 2 2 2 2 3 1 1 3 3 3];
>> [AR,RI,MI,HI]=RandIndex(A,B)
AR =
0.2429
RI =
0.6765
MI =
0.3235
HI =
0.3529
3. 参考文献
(simple) Tool for estimating the number of clusters
Mutual information and Normalized Mutual information 互信息和标准化互信息
Evaluation of clustering