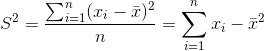OICLASS 普及组模拟测试2 题解
目录
T1 排序
T2 方差
T3 车票
T4 回家
T1 排序
此题数据存在争议，在此只讲思路，不提供代码
因要从小到大排序，而且只能换一个区间，所以只能选择一个从大到小的区间翻转，若有多个从大到小的区间则不能只翻一次就排好序
如： 1 2 3 6 5 4 7 8
我们只需把6 5 4 翻转即可，
又如：1 2 3 6 5 4 7 8 12 11 10 9 13
我们要翻两次，所以不成立
***注意：（此处是数据争议的地方）翻转后可能仍然无法成立 ，需要特判（数据没特判）。。。
如：10 11 12 5 4 3 2 14 15 16
T2 方差
化简方差公式可得 
因输出答案要乘
所以即是求L到R区间的 
快速求区间和可用前缀和，时间复杂度：读入O（n），查询O（1）
代码（C语言）
#include
int n,q;
long long a[1000006],a2[1000006],ha[1000006],ha2[1000006];
long long qa(int l,int r)
{
return ha[r]-ha[l-1];
}
long long qa2(int l,int r)
{
return ha2[r]-ha2[l-1];
}
int main()
{
scanf("%d",&n);
scanf("%d",&q);
for(int i=1;i<=n;++i)
{
scanf("%lld",&a[i]);
a2[i]=a[i]*a[i];
ha[i]=ha[i-1]+a[i];
ha2[i]=ha2[i-1]+a2[i];
}
for(int i=1;i<=q;++i)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%lld\n",qa2(l,r)*(r-l+1)-qa(l,r)*qa(l,r));
}
return 0;
}
/*
输入
3 4
1 2 2
1 1
1 2
1 3
2 3
输出
0
1
2
0
*/
T3 车票
还是前缀和。。。开数组（桶）记录其上下车时间（上车的时间点+1，下车车-1），对于每一天扫一次求每个时刻人数，输出这一天人数最大值
代码（C语言）
#include
#define max(a,b) ((a)>(b)?(a):(b))
int f[51][1000006];
int n,m,k;
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;++i)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
f[a][b]++;
f[a][c]--;
}
for(int i=1;i<=k;i++)
{
int maxans=0,sum=0;//当前车上人数 因记录上车时+1，下车时-1，所以只要扫过去就知道当前列车人数
for(int j=1;j<=n;++j)
{
sum+=f[i][j];
maxans=max(maxans,sum);
}
printf("%d\n",maxans);
}
return 0;
}
/*
10 5 3
1 1 3
1 3 5
2 1 4
1 7 8
2 2 10
*/ T4 回家
用 dijkstra 或 SPFA 记录经过每个点的次数。对于每个点，到这个点的最短路径数量为所有可以用最短路径到达这个点的点的最短路径数量总和
如样例
1->2->4 或 1->3->4 是最短的，共两条
注意：（1）单向变 （2）一边加一边取模，不然会爆int
代码（c++）写复杂了
#include
#include
#include
#include