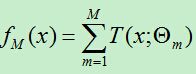理解集成学习Boosting思想之GBDT、XGBoost,附带案例
前言
前面我们介绍了使用 Boosting 思想的 AdaBoost ,它是通过前一轮决策的结果来给样本设置权重,决策正确的权重减小,决策错误的权重增加;然后将加权后的数据集输入下一个弱学习器训练,直到达到训练停止条件。
Boosting 思想的GBDT、XGBoost,在目前的竞赛和工业界中使用非常频繁,能够有效的应用到分类、回归,更是因为近几年被应用于构建搜索排序的机器学习模型而引起广泛关注。虽然用起来不难,但是要想完整理解它的原理及推导不是那么容易,本篇尽可能通过简单的方式来介绍。
一、提升树模型
提升树是以决策树为基分类器的提升方法,通常使用CART树。针对不同问题的提升树学习算法,主要区别在于使用的损失函数不同。
1)分类问题:指数损失函数。可以使用CART分类树作为AdaBoost的基分类器,此时为分类提升树。
2)回归问题:平方误差损失函数。
3)决策问题:一般损失函数。
1、提升树算法
提升树采用线性模型+前向分步算法+CART树(基函数)。提升树的加法模型可表示为:(此时树前面并没有权重!!下面有分析)
对于基函数是分类树时,我们使用指数损失函数,此时正是AdaBoost算法的特殊情况,即将AdaBoost算法中的基分类器使用分类树即可。
2)基函数是回归树
若基函数是回归树,则使用平方误差损失函数。
我们将回归树的输入空间划分为R1,R2,…,RJ个区域,每个区域的输出分别为:Cj,则回归树可以表示为:

前向分步算法第m步的得到的模型为:
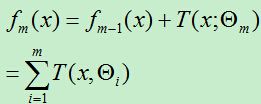
平方误差损失函数为:
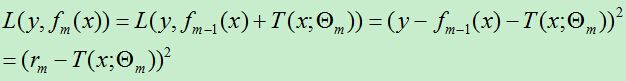
设:![]() ,rm即为当前模型拟合数据的残差。对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
,rm即为当前模型拟合数据的残差。对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
因为需要用到上一步的分类器,故而在每轮都需要计算残差,然后遍历可能的切分点,找出平方损失函数最小的切分点将输入划分为两个子集,然后依次类推,直到不能继续划分。
算法过程:
训练集为:T={(x1,y1),(x2,y2),…,(xn,yn)}。
1)初始化:f0(x)=0
2)下面共进行M轮的迭代,对于第m轮的迭代过程如下:(m=1,2,…,M)
A)遍历每个特征的每个可能取值,计算残差:
![]()
B)对于特征的每个可能取值,选择平方损失函数![]()
最小的切分点,得到树![]()
C)更新![]()
3)最终得到回归问题提升树:
在上面的算法中,并没有在每个基分类器前面加上权值,此算法通过每次减小残差的方式来减小每轮所产生的模型的损失函数,通过这种方式,逐步减小残差值来使得损失函数减小,这样的话最初的模型的损失函数应该最大,那么在最终的线性组合中应该减小它的权重,但是上述算法并没有这样做,而是将每轮产生的模型通过均值或投票的方式来产生最终的结果??
其实,在每轮的迭代过程中生成的![]() 并不是一个独立的分类器,它只是对残差的拟合,只有将它添加到前一轮的累加模型中才会对训练集有好的分类或回归效果。
并不是一个独立的分类器,它只是对残差的拟合,只有将它添加到前一轮的累加模型中才会对训练集有好的分类或回归效果。
3、损失函数最小化方法
对于最开始提到的三种损失函数,其最小化方法各有不同。当损失函数为下面几种函数时,最小化损失函数的方法如下:
1)指数函数
当损失函数为指数函数时,比如AdaBoost算法的损失函数是指数函数,这时通过前向分步算法来解决。
前向分布算法在每轮迭代时,通过将上一轮所生成的模型所产生的损失函数最小化的方法来计算当前模型的参数。
2)平方误差损失函数
在回归树提升算法中,遍历当前输入样例的可能取值,将每种可能值计算一遍损失函数,最终选择损失函数最小的值。(很原始)
在计算平方损失误差时,可能出现残差项(y-fm-1(x)),此时可以通过如下方法来进行优化:每一轮迭代是为了减小上一步模型的残差,为了减少残差,每次在残差的负梯度方向建立一个新的模型,这样一步一步的使得残差越来越小。
3)一般损失函数
对于一般损失函数,可以通过梯度下降的方法来使得损失函数逐步减小,每次向损失函数的负梯度方向移动,直到损失函数值到达谷底。
2、实例
通过数据数据进一步理解回归提升树。已知训练数据x xx的取值范围为[0.5,10.5] [0.5, 10.5][0.5,10.5],y yy的取值范围为[5.0,10.0] [5.0, 10.0][5.0,10.0],如下表:

下面就按照上面的回归问题的提升树算法来求:
考虑以下优化问题: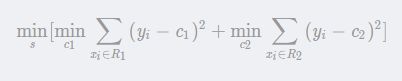
求解训练数据的切分点s:
容易求得在R1,R2 内部使平方损失误差达到最小值的c1,c2 为:
这里N1,N2 是R1,R2的样本点数。
第一步:求T1(x)
求训练数据的切分点,根据所给数据,考虑如下切分点:1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5
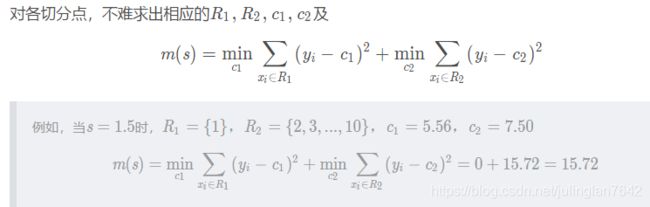
计算所有切分点s ss的m(s) m(s)m(s),如下表:


第二步:求T2(x)

重复以上步骤,求得:


假设此时已经满足误差要求,那么 f(x)=f6(x)即为所求提升树。
二、GBDT(Gradient Boosting Decison Tree)(梯度提升迭代决策树)
1、 GBDT 与 AdaBoost 的区别:
AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值,然后一轮一轮的迭代;
GBDT也是迭代,但是GBDT要求弱学习器必须是CART模型,而且GBDT在模型训练的时候,是要求模型预测的样本损失尽可能的小。
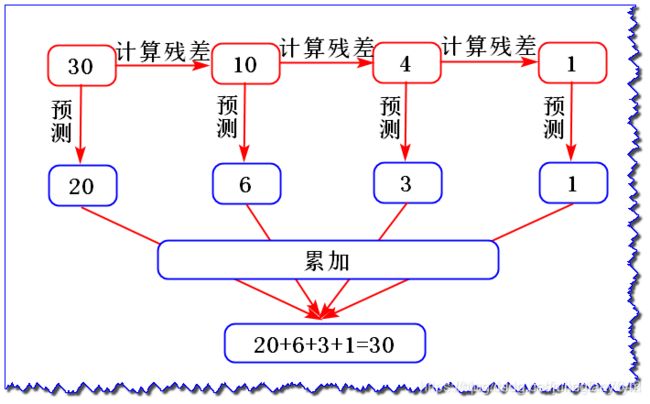
2、直观理解

3、简单实例
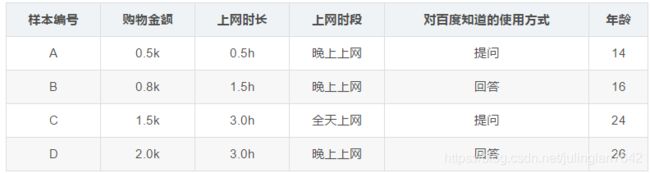
假设训练集如下:
如果按传统的决策树构建,可如下图:

对于训练集,此决策树的准确率为100%;
我们知道在构建决策树的时候,为了尽可能正确分类训练样本,节点划分过程不断重复,有时候就会导致决策树节点过多,造成模型过拟合;
假设待预测数据为:购物金额0.5k,上网时长1.5h,晚上上网,提问,14岁
传统决策树会预测为16岁
如果使用GBDT来训练

图中,上面一棵树还是按有收入是否划分,下面一棵树以前面一个数的残差作为训练样本,当新的预测值与残差相等(也就第二次计算的残差中为0的),则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄;第二棵树的残差都为0,说明所有样本都正确预测了
A:0.5k;0.5h;晚上上网;提问;预测年龄:(-1)+15=14
B:0.8k;1.5h;晚上上网;回答;预测年龄:1+15=16
C:1.5k;3.0h;全天上网;提问;预测年龄:(-1)+25=24
D:2.0k;3.0h;晚上上网;回答;预测年龄:1+25=26
其实,我们发现两个方法的准确率都是100%,那么为什么要用GBDT呢?
原因就是,传统的决策树容易过拟合,假设有个新数据待预测:购物金额0.5k,上网时长1.5h,晚上上网,提问,14岁;
传统决策树预测结果为16岁;
GBDT 预测为:(-1)+15=14岁;
现在,我们回头来看看上图,由20变为0,变化比较大,容易造成过拟合;
可以给定步长 step,在构建下一棵树的时候使用step * 残差值作为输入,这样可以避免过拟合。
三、GBDT 算法推导
GBDT由三部分构成:DT(Regression Decistion Tree)、GB(Gradient Boosting)和Shrinkage(衰减)
1、DT(Regression Decistion Tree)——回归决策树
GBDT 中的决策树都是回归树,不是分类树:
回归树:用于预测实数值,比如温度、年龄等;
分类树:用于分类标签,比如:性别、晴天/阴天、是否等;
我们知道GBDT的思想使用了集成学习,也就是将每棵决策树(弱学习器)的结果累加,得到最终结果:
如果我们将每棵回归树的预测结果相加,比如年龄:20岁+6岁+3岁+1岁=30岁 是有意的;
但是如果我们将分类树的预测结果相加,比如性别:男+女 = ? 显然无意义。
因此 GBDT 中决策树只能回归树。
2、GB(Gradient Boosting)——梯度提升
本篇一开始介绍了提升树利用加法模型与前向分步算法实现学习的优化过程。提升树使用平方误差损失和指数损失函数时,每一步优化都可以如上面的步骤简单实现。但是对于一般损失函数而言,往往每一步优化并不那么容易,针对这个问题,Freidman提出了梯度提升算法,这是利用最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值。

1)假设第m-1轮强学习器为
损失函数为:![]()
(2)第m轮强学习器为: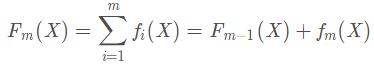
损失函数为: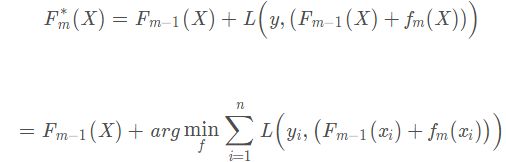
其中,n 为样本数


3、Shrinkage(衰减)
基本思想就是:
\quad\quad每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。换句话说缩减思想不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分,只有通过多学几棵树才能弥补不足。
Shrinkage仍然以残差作为学习目标,但由于它采用的是逐步逼近目标的方式,导致各个树的残差是渐变的而不是陡变的。之所以这样做也是基于模型过拟合的考虑。
四、GBDT 案例
sklearn 库 ensemble.GradientBoostingRegressor 类API:
sklearn.ensemble.GradientBoostingRegressor(loss=’ls’, learning_rate=0.1,
n_estimators=100, subsample=1.0, criterion=’friedman_mse’, min_samples_split=2,
min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3,
min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None,
max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False,
presort=’auto’, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001)
五、XGBoost
1、简介
XGBoost 是 GBDT 的升级版,前面介绍到,GBDT 是一种基于 Boosting 集成思想的学习器,并采用梯度提升的方法进行每一轮的迭代最终组合出强学习器,这样的话算法的运行往往要生成一定数量的树才能达到令我们满意的准确率。当数据集大且较为复杂时,运行一次极有可能需要几千次的迭代运算,这将对我们使用算法造成巨大的计算瓶颈。
针对这一问题,华盛顿大学的陈天奇博士开发出了 XGBoost ,XGBoost 最大的特点在于它能够自动利用CPU的多线程进行并行计算,同时在算法上加以改进,极大地提升了模型训练速度和预测精度。
2、目标函数

引入正则化项是因为我们的目标是希望生成的模型的泛化性能比较好,能够很好的预测新数据,而不是简单的拟合训练集的结果(这样会导致过拟合);
需要在保证模型“简单”的基础上最小化训练误差,这样得到的参数才具有好的泛化性能;
正则项就是用于惩罚复杂模型,避免预测模型过分拟合训练数据,常用的正则有 L1 L2正则

3、XGBoost 推导过程
这里先给出一些数据,以便接下来使用;假设有如下数据,判断谁愿意去玩游戏:
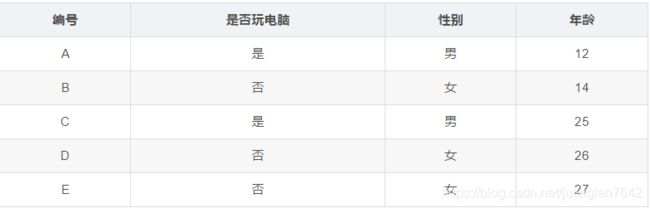

图中权重表示该人愿意去玩游戏的得分,得分越大越愿意;得分为负,表示不愿意
最终A的得分为2.9,B的得分为-0.8,C的得分为-0.1,D的得分为-1.9,E的得分为-1.9;
1目标函数构建



具体计算如下图:





集成学习Stacking思想
集成学习除了Bagging、Boosting思想,还有Stacking,此处只提一下,不做具体介绍,因为现在基本不使用了。
\quad\quadStacking是指训练一个模型用于组合(combine)其它模型(基模型/基学习器)的技术。即首先训练出多个不同的模型,然后再以之前训练的各个模型的输出作为输入来新训练一个新的模型,从而得到一个最终的模型。一般情况下使用单层的Logistic回归作为组合模型。
Stacking 跟现在比较火的深度学习很相似,所以现在一般不使用Stacking
部分内容来源于:
原文链接:https://blog.csdn.net/Daycym/article/details/84593744