统计学习方法笔记---感知机

感知器

本章概要

1. 感知器是根据输入实例的特征向量x对其进行二类分类的线性分类模型：
   $$f(x)=sign(w\cdot x+b)$$
   感知器模型对应于输入空间中的分离超平面$w\cdot x+b=0$
2. 感知器学习的策略是极小化损失函数：
   $$mi{n}_{w,b}L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
   损失函数对应于误分类点到分离超平面的总距离，若$y_i(w\cdot x_i+b)<0$ 则为误分类点，M为误分类点的集合 。
3. 感知器学习算法是基于随机梯度下降法的对损失函数的最优化模型，有原始形式和对偶形式。算法简单且易于实现。原始形式中，首先任意选取一个超平面，然后利用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降
4. 当训练数据集线性可分时，感知器学习算法是收敛的。感知器算法在训练数据集上的误分类次数K满足不等式：
   $$k\le (\frac{R}{\gamma }{)}^2$$
   当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解可有由于不同的初始值或不同的迭代顺序而有所不同。

基本算法

极小化损失函数：采用随机梯度下降，在极小化的过程中，不是一次使分类点集合M中所有的误分类点的梯度下降，而是随机选取一个误分类点使其梯度下降

原始形式每一次迭代需要重新计算$w,b$，计算量较大。

对偶形式每一次迭代只需要计算${\alpha }_i$ 和 $b$，当学习率为1时，${\alpha }_i$表示第i个实例由于误分类需要更新的次数。

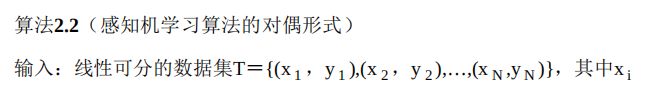
感知器的收敛性

收敛性：有限迭代次数内，得到一个能将数据集全部分类正确的分离超平面和感知器模型

作业

1.思考感知机模型假设空间是什么？模型复杂度体现在哪里？

感知器是一种线性分类模型，属于判别模型，
感知机模型的假设空间是定义在特征空间中的所有**线性分类模型**，即：

$$WX+b=0$$

模型复杂度体现为数据的维度X(X1,X2,...Xd)

2.已知训练数据集D，其正实例点是x1=(3,3)T,x2=(4,3)T，负实例点是x3=(1,1)T:

(1) 用python 自编程实现感知机模型，对训练数据集进行分类，并对比误分类点选择次序不同对最终结果的影响。可采用函数式编程或面向对象的编程。

误分类点的选择不同，决策边界也不同。

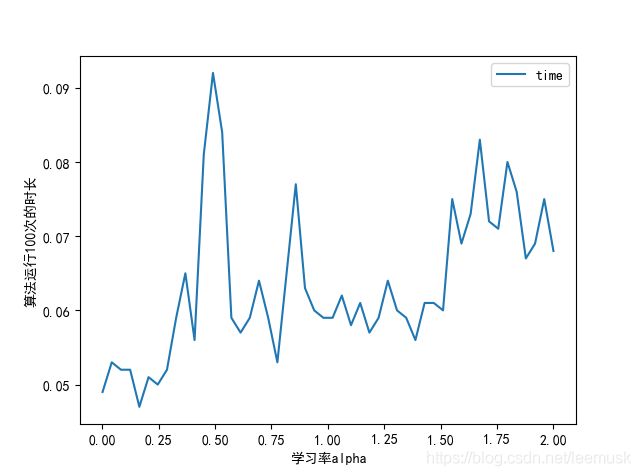
(2)试调用sklearn.linear_model 的Perceptron模块，对训练数据集进行分类，并对比不同学习率h对模型学习速度及结果的影响。

学习率对模型的结果没有影响，因为w,b的初始值都设为0，最终值都是学习率的整数倍，最后公式将可将学习率约掉,则与学习率无关。
学习率与训练时间为波动性。

(3)附加题：

对比传统感知机算法及其对偶形式的运行速度。

 传统感知器的运行速度有数据的特征数量即维度d决定，对偶形式有数据的样本数量决定

代码结果如下：
(1) python 自编程

import numpy as np 
import matplotlib.pylab as plt

# 主函数
def main():
    # 构造训练数据集 numpy array
    x_train = np.array([[3,3],[4,3],[1,1]])
    y = np.array([1,1,-1])

    #构建感知器对象，对数据集进行训练
    perception = MyPerceptron()
    perception.fit(x_train,y)
    print(perception.w)
    print(perception.b)

    #结果图像绘制
    draw(x_train, y, perception.w ,perception.b)
    print("success")

class MyPerceptron:
    def __init__(self):
        # w参数定义为None，因为没有给定训练参数，所以无法得知X的特征维度，即w的维度
        self.w = None
        self.b = 0
        self.rate = 1

    # 核心算法实现
    def fit(self, x_train, y):
        # 用样本点的特征数更新初始w，如x1=(3,3),有两个特征。
        self.w = np.zeros(x_train.shape[1])
        i = 0
        while i < x_train.shape[0]:
            # 可以选择决定误分类点的不同选择顺序
            X = x_train[x_train.shape[0] - i -1]
            Y = y[x_train.shape[0] - i -1]
            if Y*(np.dot(self.w, X) + self.b) <= 0:
                self.w = self.w + self.rate * np.dot(Y,X)
                self.b = self.b + self.rate * Y
                # 如果是误判点，从0开始检测
                i = 0
            else:
                i += 1

def draw(x, y, w, b):
    postive = x[y == 1]
    negtive = x[y == -1]
    plt.plot(postive[:,0], postive[:,1],'b+', label='+1')
    plt.plot(negtive[:,0], negtive[:,1], 'r*', label ='-1')
    plt.legend()
    
    if w[1] != 0 and w[0] != 0:
        x = np.linspace(0,5,10)
        y = -x * w[0] / w[1] - b / w[0] #决策边界的方程应为：w[0]x1 + w[1]x2 + b = 0
        plt.plot(x, y, 'r', linestype='--')
    elif w[1] == 0:
        plt.axvline(-b / w[0],color='red',linestyle='--')
    else:
        plt.axhline(-b / w[1],color='red',linestyle='--')
    
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.show()

main()

(2) 调用sklearn.linear_model 的Perceptron模块

from sklearn.linear_model import Perceptron
import numpy as np
# 定义数据集
x_train = np.array([[3,3],[4,3],[1,1]])
y = np.array([1,1,-1])

# 新建Perceptron对象
myPerceptron = Perceptron()

# 训练数据集
myPerceptron.fit(x_train,y)

# 输出模型参数
print("coef: ", myPerceptron.coef_, "intercept: ", myPerceptron.intercept_)

# 输出模型预测的准确率
res = myPerceptron.score(x_train, y)
print("precision: {:.0%}".format(res))