动态规划求概率期望和高斯消元求解方程组
算法课的project有一道很有意思的题目,是用动态规划求概率期望,其中用到了高斯消元法,特此记录一下。
题目:
小 Z 来到一个古墓去寻找宝藏。 古墓中有非常多的路口和岔路, 有些路口有陷阱, 小 Z 在每次经过路口 i 的陷阱的时候都要掉 A[i]点血, 而且陷阱是永久有效的(即小 Z 每到一次路口 i 就要掉 A[i]点血) 。 幸运的是, 有一些路口没有陷阱。 可不幸的是, 小 Z 是个路痴, 他完全无法判断他走过哪里, 要去哪里; 他只能在每一个路口随机(等概率地) 走向某一条岔路到达下一个路口。 小 Z 现在在古墓的入口处(即路口 1) , 这里没有陷阱; 宝藏藏匿在路口 n, 那里也没有陷阱。
而你万万没有想到的是, 你是这个古墓的守护者。 你知道这个古墓所有的构造(包括它的路口、 岔路和陷阱的情况) , 现在你需要计算出小 Z 能活着见到宝藏的概率。
现给出了该函数的接口:
double func(int n, int hp, vector<int>& damage, vector<int>& edges) {
}
其中参数 n 是路口数量; hp 是小 Z 的初始血量; 数组 damage 是 n 个数据,代表 n 个路口陷阱的伤害(无陷阱处为 0, 保证路口 1 和 n 处无陷阱) ; 数据edges 是 2*(岔路条数) 个数据, 每 2 个数据是一条边, 边都是双向的。
举个例子:
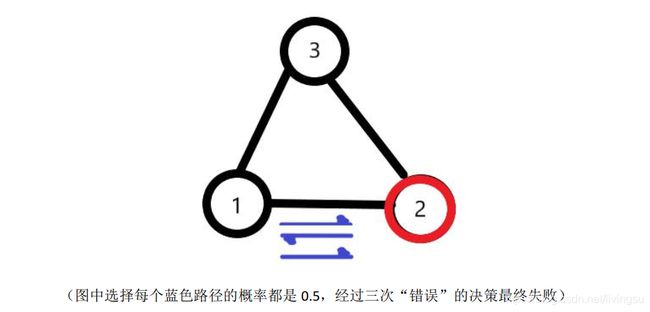
有个三角形路口 1, 2, 3。 小 Z 有 2 点血。 小 Z 在 1, 宝藏在 3, 陷阱在 2(伤害为 1) 。 那么它的结果为 0.875。 小 Z 在血量降到 0 之前走到 3 就算成功, 所以它失败的唯一路径是 1-2-1-2, 每次寻路都是随机的, 三次都走错的概率是 0.5^3 = 0.125, 那么成功走到 3 的概率就是 0.875。
示例输入:
3 2 3
0 1 0
1 2
1 3
2 3
n=3,hp=2,有3条边,damage[]={0,1,0},边是1->2,1->3,2->3,edges[]={1,2,1,3,2,3}。
思路:
建立二维数组dp[hp+1][n+1],其中dp[i][j]表示剩下i滴血时到达j点的期望次数。列出状态转移方程:

i=hp,j=1的时候要加1,因为开始点是节点1,所以必然会经过1次节点1。不包括终点的意思是:一旦到达终点就结束了,所以不能考虑到了终点又折返。
当damage[j]>0的时候,若将下面层均视为常数,则可以很轻松的求出dp[i][j]。而当damage[j]=0时,在这一hp层的所有damage为0的路口的dp值是相互有一个关系(即方程)的,不能直接求出值。要首先求出这一层damage不为0的路口dp值,将它们视为常数,然后利用高斯消元法求解damage=0的路口dp的线性方程组,就可以求出这一hp层的所有dp值。这一层求出来以后,就可以继续求解上一层。
最后,小Z能活着见到宝藏的概率是

即当hp>=1时,到达路口n的期望次数之和。
代码:
//选择列主元并进行消元
void upperTrangle(vector<vector<double>> &a,int n) {
double tmp; //用于记录消元时的因数
for (int i = 1; i <= n; i++) {
int r = i;
for (int j = i + 1; j <= n; j++)
if (fabs(a[j][i]) > fabs(a[r][i]))
r = j;
if (r != i)
for (int j = i; j <= n + 1; j++)
swap(a[i][j], a[r][j]);//与最大主元所在行交换
for (int j = i + 1; j <= n; j++) {//消元
tmp = a[j][i] / a[i][i];
for (int k = i; k <= n + 1; k++)
a[j][k] -= a[i][k] * tmp;
}
}
}
//高斯消元法(列选主元)
void Gauss(vector<vector<double>> &a, int n) {
upperTrangle(a, n);//列选主元并消元成上三角
for (int i = n; i >= 1; i--) {//回代求解
for (int j = i + 1; j <= n; j++)
a[i][n + 1] -= a[i][j] * a[j][n + 1];
a[i][n + 1] /= a[i][i];
}
}
vector<int> findAdjacent(vector<int> edges, int p) {//找p点的相邻点
vector<int> points;
for (int i = 0; i < edges.size() / 2; ++i) {
if (edges[2 * i] == p) {
points.push_back(edges[2 * i + 1]);
}
else if (edges[2 * i + 1] == p) {
points.push_back(edges[2 * i]);
}
}
return points;
}
double func(int n, int hp, vector<int>& damage, vector<int>& edges) {
vector<vector<double>> dp;
for (int i = 0; i < hp + 1; ++i) {
vector<double> tmp;
for (int j = 0; j < n + 1; ++j) {
tmp.push_back(0);
}
dp.push_back(tmp);
}
dp[hp][1] = 1;
vector<int> adjacentCount;//邻接点个数,下标是点标识
for(int i=0;i<=n;++i){
if(i==0) adjacentCount.push_back(0);
else adjacentCount.push_back(findAdjacent(edges,i).size());
}
for (int row = hp; row >= 1; --row) {
//先计算damage不为0的点
for (int col = 1; col <= n; ++col) {
if (damage[col - 1] > 0) {
for (int i : findAdjacent(edges, col)) {//不为终点的相邻点
if (i != n && row + damage[col - 1] <= hp) {
dp[row][col] += dp[row + damage[col - 1]][i]/(double)adjacentCount[i];
}
}
}
}
//计算damage为0的点
vector<int> zero;
vector<vector<double>> matrix;//增广矩阵的扩大
for (int col = 1; col <= n; ++col) {
if (damage[col - 1] == 0) {
zero.push_back(col);
}
}
for (int i = 0; i < zero.size() + 1; ++i) {//矩阵n+1行 n+2列 第1行第1列均为0 其余部分为增广矩阵
vector<double> tmp;
for (int j = 0; j < zero.size() + 2; ++j) {
tmp.push_back(0);
}
matrix.push_back(tmp);
}
//填充增广矩阵
for (int i = 0;i<zero.size();++i){
matrix[i + 1][i + 1] = -1;
matrix[i+1][zero.size() + 1] = -dp[row][zero[i]];//常数项
for (int k : findAdjacent(edges, zero[i])) {
if (k != n) {
if (damage[k-1] > 0) {//若damage>0,则为常数项
matrix[i+1][zero.size() + 1] -= dp[row][k]/(double)adjacentCount[k];
}
else {//若damage=0,则为未知项
for (int index = 0; index < zero.size(); ++index) {
if (zero[index] == k) {
matrix[i+1][index + 1] = 1/(double)adjacentCount[k];
break;
}
}
}
}
}
}
//高斯消元法求解
Gauss(matrix, zero.size());
//将解写回dp中
for (int i = 0; i < zero.size(); ++i) {
dp[row][zero[i]] = matrix[i + 1][zero.size() + 1];
}
}
double result = 0;
for (int i = 1; i <= hp; ++i) {
result += dp[i][n];
}
return result;
}
时间复杂度是O(hp*n^2),空间复杂度是O(hp*n)。