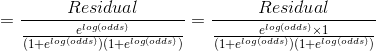集成算法学习（3）-Boosting(GBDT分类)（举例说明，通俗易懂）

通过前面两贴Bagging、Boosting(AdaBoost)原理与公式推导和Boosting(GBDT回归)（举例说明，通俗易懂）对GBDT有了大致了解，这帖就来讲一讲GBDT分类。

GBDT分类是对类别变量进行分类。

还是通过例子了解。

1、案例讲解

总共有 6 个样本，每个样本有三个属性 Likes Popcorn，Age，Favorite Color，对每个样本是否 Loves Troll 2 进行判别。

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2
1	Yes	12	Blue	Yes
2	Yes	87	Green	Yes
3	No	44	Blue	No
4	Yes	19	Red	No
5	No	32	Green	Yes
6	No	14	Blue	Yes

1）初始化 

因为GBDT分类使用的是逻辑函数，逻辑函数的平均值是某一类样本数/另一类样本数（odds）。该例中预测变量 Loves Troll 2 有4个 Yes，2个 No，因此初始叶结点的预测值 。

对于odds的理解，大家可以看一下这篇逻辑回归（含推导）里面有详细的讲解。

就像逻辑回归，  (范围在0-1）用于分类的最简单方式就是将其转化为概率，在GBDT中叫逻辑方程（Logistic Function）。

                                           

                                                                                   

因为，因此可以将所有训练样本预测为yes，即所有人都 Loves Troll 2。

在分类中0.5是常用的阈值，也可以选其他值。

第一次迭代（建第一棵树）：

2）计算残差 

初始预测值将所有样本都预测为 Yes，但在训练样本中有两个No，因此初始预测值不是很准，此时需要引入伪残差。

在逻辑回归中 ，因此 Yes 的概率值用 1，No 的概率值用 0 表示，如下表所示：

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2	概率
1	Yes	12	Blue	Yes	1	0.3 = 1-0.7
2	Yes	87	Green	Yes	1	0.3
3	No	44	Blue	No	0	-0.7
4	Yes	19	Red	No	0	-0.7
5	No	32	Green	Yes	1	0.3
6	No	14	Blue	Yes	1	0.3

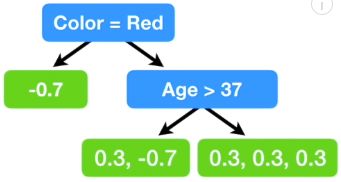
3）建树，用 Likes Popcorn，Age，Favorite Color 去预测 Residuals，构建的树如下所示：

                                                         

注意：GBDT不论是回归还是分类，叶结点的数量都是有限制的。

4) 对叶结点的值进行转换

类似回归，预测值都是用前面的预测值加上残差预测，但是分类中的预测值是 ，因此无法直接与残差预测值相加，如下图：

                                                 

如上图所示，预测值   与第一分支的叶结点值-0.7是无法直接相加的，因此残差需要转换：

                      单个叶结点的残差转换：              

 这是单个叶结点的所有残差和以及单个叶结点的单个样例的前一个模型的预测值 。

对于第一个叶结点（从左往右）只有一个值，因此转换后的值 =

第二个叶结点：

第三个叶结点：

上面就是三个叶结点的输出值。

5）计算预测值（概率）

正常情况下会在决策树前面加一个学习率，学习率正常取0.1，具体原因可以看一下GBDT回归那一帖。

， 代表学习率

                                    

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2	概率	Transformed		(概率值）
1	Yes	12	Blue	Yes	1	1.4	1.8	0.9（Yes)
2	Yes	87	Green	Yes	1	-1	-0.1	0.5（Yes)
3	No	44	Blue	No	0	-1	-0.1	0.5（Yes)
4	Yes	19	Red	No	0	-3.3	-1.94	0.1（No)
5	No	32	Green	Yes	1	1.4	1.8	0.9（Yes)
6	No	14	Blue	Yes	1	1.4	1.8=0.7+0.8*1.4

第二次迭代（建第二棵树）：

22) 计算残差 

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2	概率	(概率值）
1	Yes	12	Blue	Yes	1	0.9	0.1=1-0.9
2	Yes	87	Green	Yes	1	0.5	0.5
3	No	44	Blue	No	0	0.5	-0.5
4	Yes	19	Red	No	0	0.1	-0.1
5	No	32	Green	Yes	1	0.9	0.1
6	No	14	Blue	Yes	1		0.1

23）建树

                                           

24) 对叶结点的值进行转换

         第一个叶结点：

         第二个叶结点：

         第三个叶结点：      

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2	概率		Transformed
1	Yes	12	Blue	Yes	1	0.1=1-0.9	0.6
2	Yes	87	Green	Yes	1	0.5	2
3	No	44	Blue	No	0	-0.5	-2
4	Yes	19	Red	No	0	-0.1	0.6
5	No	32	Green	Yes	1	0.1	0.6
6	No	14	Blue	Yes	1	0.1	0.6

25）计算预测值（概率）

 

num	Likes Popcorn	Age	Favorite Color	Loves Troll 2	概率	Transformed	Transformed		(概率值）
1	Yes	12	Blue	Yes	1	1.4	0.6	2.3=0.7+0.8*1.4+0.8*0.6
2	Yes	87	Green	Yes	1	-1	2	1.5	0.8
3	No	44	Blue	No	0	-1	-2	-1.7	0.2
4	Yes	19	Red	No	0	-3.3	0.6	-1.46	0.2
5	No	32	Green	Yes	1	1.4	0.6	2.3	0.9
6	No	14	Blue	Yes	1	1.4	0.6	2.3	0.9

第三次迭代：

计算残差......

残差会越来越小

2、具体步骤讲解

由上总结GBDT分类的具体步骤如下：

1）

这一步确定样本和损失函数。

n 是样本数量，i 代表第几个样本， 代表属性， 代表观测类别概率值。

GBDT 分类中损失函数主要有  最大似然函数：  

 是 预测概率值。

因为损失函数是对预测值求导，而这里指的预测值是指 ，所以需要将上式转换为  的损失函数而不是预测概率p的损失函数。

因为上面的是求最大值，因此在前面加个负号，求最小值，如下所示：

   

   

    

    

    

     

     

接下来对损失函数微分：

                    

                    

2）

这一步得到所有样本的最佳初始 。

最小化观测值与预测概率  值之间的误差并对微分即可得到观测值的最佳初始。

  是观测值， 是常数 (这里用来代替初始) ， 表示初始。

          

                                       

计算 ：

3）

这一步，建立M 棵树。

这一步计算所有样本的第 m 棵树的残差。

 是损失函数的导数也叫梯度，F是（上一棵树的），

在  前面加个负号，这就是负向梯度， ，就是上面例子的 ，用  表示。

 代表第 m 棵树第  i 个样本的伪残差（为了区别于线性回归的残差）。

这一步根据 (A) 计算的残差构建树。注意每个叶结点都要有数据，不能为空。

j 代表第 m 棵树的第 j 个结点。

这一步对叶结点的残差值进行转换，跟上面例子中的 24）对叶结点的值进行转换一致。

 表示第 j 个叶结点残差， 表示第 j 个叶结点的观测值， 表示第 j 个叶结点 ， 是常数(用来替代第 j 个叶结点的残差转换后的值）。

对于每个结点都有一个最优残差值  是 第 j 个叶结点的观测值   与 (第 j 个叶结点 +第 j 个叶结点的残差转换值 ) 之间的最小误差。因此通过损失函数对 微分即可找到每个结点的最优残差转换值 。

假设第m棵树第1个叶结点有l个残差，则：

                                                

对上面的  求导会很繁琐，因此用二阶Taylor Polynomial 近似的代替损失函数。

                             

                              

                         

                                                         

                                                             

                                                             

                                                             

                                                             

                                                             

假设第m棵树第1个叶结点有l个残差，则：

                                                      

这一步计算新的 ，

4) 误差低于阈值或达到迭代次数，返回，然后算出预测的概率值，根据概率的阈值将其归到相应的类别。

 

参考：StatQuest with Josh Starmer