【线段树】CF #458 (Div. 1 + Div. 2, combined) D Bash and a Tough Math Puzzle

经典数据结构之线段树
介于复制粘贴文本过来后甚是难看的缘故，截个屏搬图片过来吧，嘿嘿
再来一个原网站地址：D-Bash and a Tough Math Puzzle


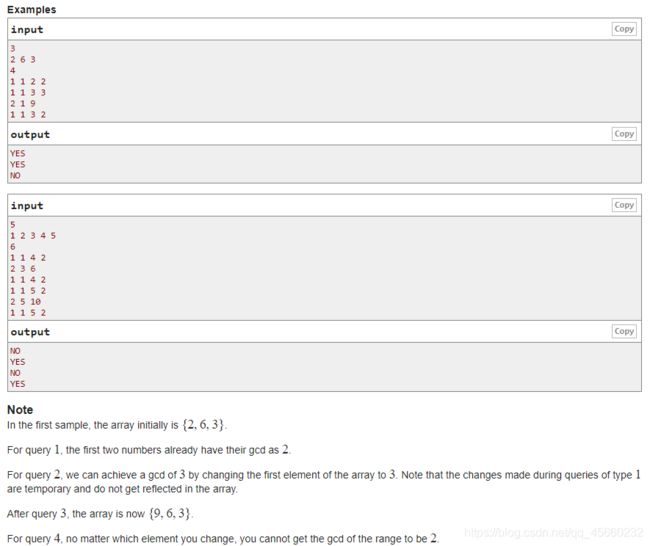
吐槽：光光学长讲太好了，讲的非常清楚，我竟然听懂了，哈哈哈，推一波他博客：光光学长博客

在这里我再来梳理一遍思路，以加深印象。
首先需要明确题意：给一个数组，在这里我们不妨用$arr$来表示;给定一个数$q$,表示$q$次询问，每一次询问可对应一种操作，一共有两种操作：$1:$询问区间 [$l$,$r$]中是否可以通过至多更改一个元素来满足给定的$x$是这个区间内所有数的最大公约数。$2:$更改原数组$arr$中的一个元素。

思路梳理：显然就是线段树的操作，对于第$2$种操作就不过多解释了，就是线段树的单点修改操作。重点来说一下第$1$种操作，要想满足$x$是区间[$l$,$r$]中在经过至多一次更改后是所有元素的最大公约数，假设这个区间内有$n$个元素，则必定要满足至少有$n-1$个元素能够整除$x$,即满足$arr[i]$%$x$==0的元素个数大于等于$n-1$个.

想必到这里肯定也会产生一个疑问，全部能够整除$x$就一定是最大公约数吗？例如下面的这个例子：
如果[$l$,$r$]中的元素是：
$4$，$8$，$12$，$16$. 明显这些元素在不进行更改的情况下最大公约数是$4$.

而此时如果$x$的值是$2$,对于区间内每个元素都能够整除，但$2$并不是最大公约数，想一下，这个是没有进行更改操作的情况，如果进行一次更改操作呢，显然一定能够满足条件。
所以对于这个问题就不需要顾虑了，只要能有大于等于$n-1$个元素满足%$x$==0就可。

注意下方的$n$非上方的$n$,下方的$n$指的是$arr$数组中的元素个数;，至于为什么不换个变量，因为我爱$n$,爱的深沉，哈哈哈哈哈

但是想一想，在查询的时候最多要判断$n-1$元素的对吧，这样的话时间复杂度就是$O(n\ast logn)$,时间复杂度过大，不太好，经过学长的测试也确实是超时了，接下来考虑一下优化，但是在哪里优化呢，$logn$这个肯定是优化不了了，所以就考虑将n这个值缩小；怎么缩小呢？来，下方见解释：
在判断的时候判断$2$个元素不能整除$x$总比判断$n-1$个元素能整除$x$快吧，具体的话，我也说不太清楚，从表面上看确实是这样。

好，这样就给化简为查询一个区间内有多少个不能整除$x$,大于或等于$2$个就t跳出输出$NO$,否则，输出$YES$.
对了，树中就存储一段区间的GCD.

写的有点啰嗦，别介哈，我都不介的，哼！

上代码：

#include
using namespace std;
const int N = 500010;
int a[N], n;
struct segment_tree {
	int l, r, val;//val记录区间内所有数的最大公约数
}tree[4 * N];
//求GCD
int gcd(int x, int y)
{
	if (y == 0) return x;
	else return gcd(y, x % y);
}
//更新父节点
void pushup(int node)
{
	tree[node].val = gcd(tree[2 * node].val, tree[2 * node + 1].val);
}
//建树
void build_tree(int node, int start, int ends)
{
	tree[node].l = start, tree[node].r = ends;
	if (start==ends)
	{
		tree[node].val = a[start];
		return;
	}
	int mid = (tree[node].l + tree[node].r) / 2;
	build_tree(2 * node, start, mid);
	build_tree(2 * node + 1, mid + 1, ends);
	pushup(node);
}
//更新叶子节点
void update(int node, int idx, int val)
{
	if (tree[node].l == idx && tree[node].r == idx)
	{
		tree[node].val = val;
		return;
	}
	int mid = (tree[node].l + tree[node].r) / 2;
	if (idx <= mid) update(2 * node, idx, val);
	else update(2 * node + 1, idx, val);
	pushup(node);
}
//查询操作
int tmp;
void query(int node, int L, int R,int x)
{
	if (tmp >= 2) return;
	if (tree[node].l==tree[node].r)
	{
		if (tree[node].val % x) tmp++;
		return;
	}
	int mid = (tree[node].l + tree[node].r) / 2;
	if (L <= mid && tree[node * 2].val % x) query(2 * node, L, R, x);
	if (R > mid&& tree[node * 2 + 1].val% x) query(2 * node + 1, L, R, x);
}
int main()
{
	scanf("%d",&n);
	for (int i = 1;i <= n;i++)
	{
		scanf("%d",&a[i]);
	}
	build_tree(1, 1, n);
	int q;
	scanf("%d",&q);
	while (q--)
	{
		int type;
		scanf("%d",&type);
		if (type == 1)
		{
			int l, r, x;
			tmp = 0;
			scanf("%d%d%d",&l,&r,&x);
			query(1, l, r, x);
			if (tmp <= 1) puts("YES");
			else puts("NO");
		}
		else {
			int idx, val;
			scanf("%d%d",&idx,&val);
			update(1, idx, val);
		}
	}
	return 0;
 
}