DBSCAN方法及其应用

1. DBSCAN密度聚类

1. DBSCAN算法是一种基于密度的聚类算法。
   
   • 聚类的时候不需要预先指定簇的个数。
   • 最终的簇的个数不定。

2. DBSCAN算法将数据点分为三类。

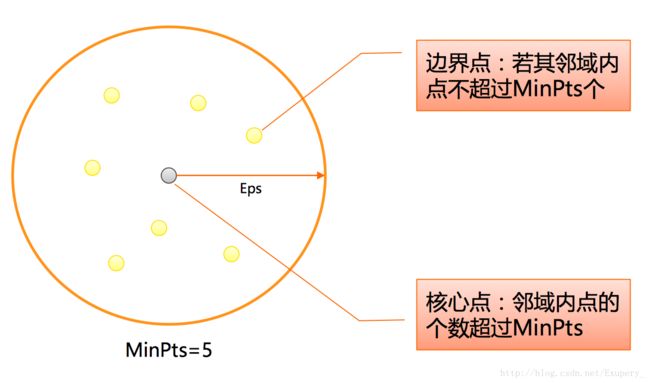
   • 核心点：在半径Eps内含有超过MinPts数目的点。
   • 边界点：在半径Eps内点的数目小于MinPts，但是落在核心点的临域内。
   • 噪音点：既不是核心点也不是边界点的点。

3. DBSCAN算法流程

   • 将所有点标记为核心点、边界点或噪声点。
   • 删除噪声点。
   • 为距离在Eps之内的所有核心点之间赋予一条边。
   • 每组连通的核心点形成一个簇。
   • 将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）。

2. 举例

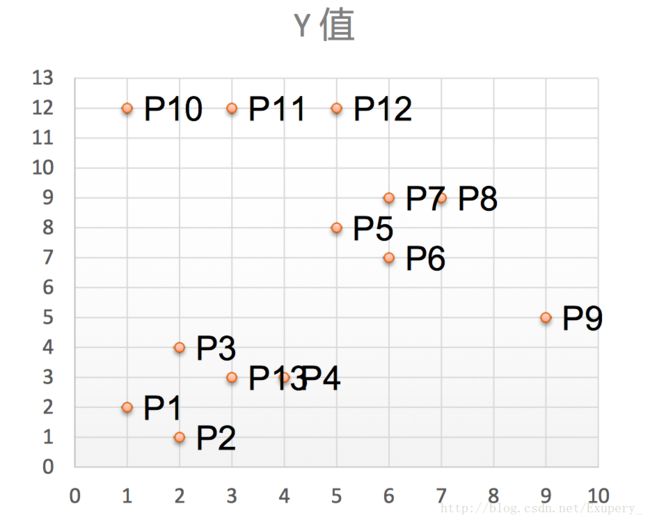
有如下13个样本点，使用DBSCAN进行聚类。

取Eps=3，MinPts=3，依 据DBSACN对所有点进行聚类 （曼哈顿距离）。

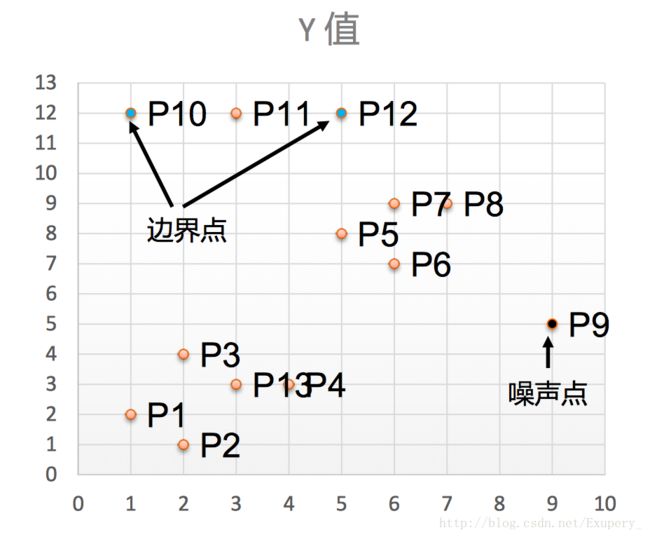
• 对每个点计算其邻域Eps=3内的点的集合。
• 集合内点的个数超过MinPts=3的点为核心点。
• 查看剩余点是否在核心点的邻域内，若在，则为边界点，否则为噪声点。

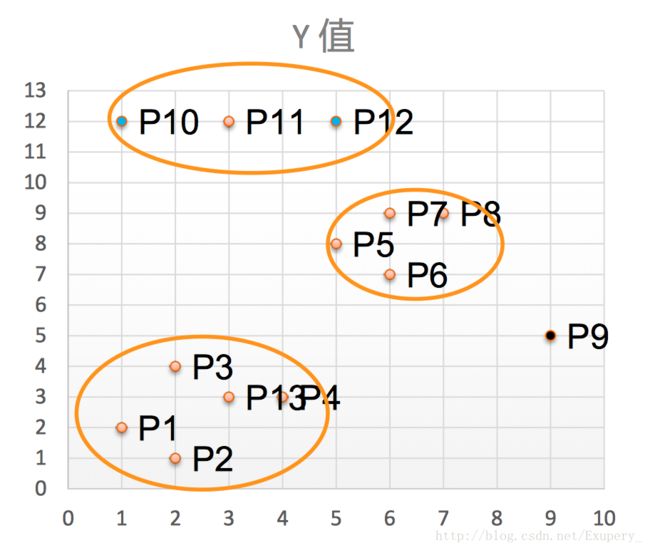
将距离不超过Eps=3的点相互连接，构成一个簇，核心点邻域内的点也会被加入到这个簇中。 则形成3个簇。

应用实例

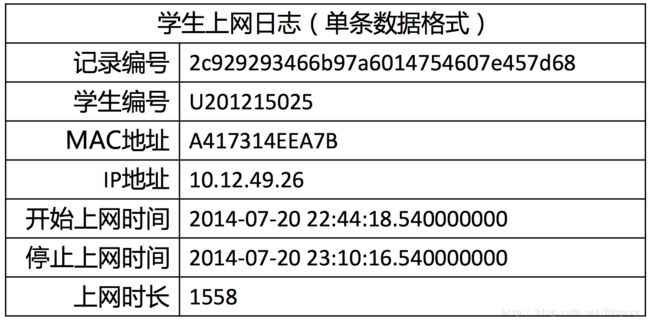
现有大学校园网的日志数据，290条大学生的校园网使用情况数据，数据包 括用户ID，设备的MAC地址，IP地址，开始上网时间，停止上网时间，上 网时长，校园网套餐等。利用已有数据，分析学生上网的模式。目的：通过DBSCAN聚类，分析学生上网时间和上网时长的模式。

数据实例

数据链接

DBSCAN主要参数

• eps：两个样本被看作邻居节点的最大距离。
• min_sample：簇的样本数。
• metric：距离计算方式。

根据上网时间聚类

import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
import matplotlib.pyplot as plt

mac2id = dict()
online_times = []
#f = open('E:/Anaconda/DATA/TestData.txt', encoding='utf-8')
f = open('E:/Anaconda/DATA/TestData.txt','r')
for line in f:

    # 读取每条数据中的mac地址，
    # 开始上网时间，上网时长

    mac = line.split(',')[2]
    online_time = int(line.split(',')[6])
    start_time = int(line.split(',')[4].split(' ')[1].split(':')[0])

    # mac2id是一个字典：
    # key是mac地址
    # value是对应mac地址的上网时长以及开始上网时间（精度为小时）

    if mac not in mac2id:
        mac2id[mac] = len(online_times)
        online_times.append((start_time, online_time))
    else:
        online_times[mac2id[mac]] = [(start_time, online_time)]

# -1:根据元素的个数自动计算此轴的长度
# X：上网时间
real_X = np.array(online_times).reshape((-1, 2))
X = real_X[:, 0:1]

# 调用DBSCAN方法进行训练，
# labels为每个数据的簇标签

db = skc.DBSCAN(eps=0.01, min_samples=20).fit(X)
labels = db.labels_

# 打印数据被记上的标签，
# 计算标签为-1，即噪声数据的比例。

print('Labels:')
print(labels)
raito = len(labels[labels[:] == -1]) / len(labels)
print('Noise raito:', format(raito, '.2%'))

# 计算簇的个数并打印，评价聚类效果

n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
print('Estimated number of clusters: %d' % n_clusters_)
print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(X, labels))

# 打印各簇标号以及各簇内数据

for i in range(n_clusters_):
    print('Cluster ', i, ':')
    print(list(X[labels == i].flatten()))

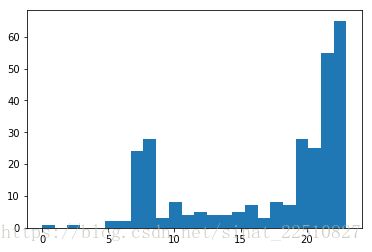
# 画直方图，分析实验结果

plt.hist(X, 24)
plt.show()

输出：

Labels:
[ 0 -1  0  1 -1  1  0  1  2 -1  1  0  1  1  3 -1 -1  3 -1  1  1 -1  1  3  4
 -1  1  1  2  0  2  2 -1  0  1  0  0  0  1  3 -1  0  1  1  0  0  2 -1  1  3
  1 -1  3 -1  3  0  1  1  2  3  3 -1 -1 -1  0  1  2  1 -1  3  1  1  2  3  0
  1 -1  2  0  0  3  2  0  1 -1  1  3 -1  4  2 -1 -1  0 -1  3 -1  0  2  1 -1
 -1  2  1  1  2  0  2  1  1  3  3  0  1  2  0  1  0 -1  1  1  3 -1  2  1  3
  1  1  1  2 -1  5 -1  1  3 -1  0  1  0  0  1 -1 -1 -1  2  2  0  1  1  3  0
  0  0  1  4  4 -1 -1 -1 -1  4 -1  4  4 -1  4 -1  1  2  2  3  0  1  0 -1  1
  0  0  1 -1 -1  0  2  1  0  2 -1  1  1 -1 -1  0  1  1 -1  3  1  1 -1  1  1
  0  0 -1  0 -1  0  0  2 -1  1 -1  1  0 -1  2  1  3  1  1 -1  1  0  0 -1  0
  0  3  2  0  0  5 -1  3  2 -1  5  4  4  4 -1  5  5 -1  4  0  4  4  4  5  4
  4  5  5  0  5  4 -1  4  5  5  5  1  5  5  0  5  4  4 -1  4  4  5  4  0  5
  4 -1  0  5  5  5 -1  4  5  5  5  5  4  4]
Noise raito: 22.15%
Estimated number of clusters: 6
Silhouette Coefficient: 0.710
Cluster  0 :
[22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22]
Cluster  1 :
[23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23]
Cluster  2 :
[20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
Cluster  3 :
[21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21]
Cluster  4 :
[8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]
Cluster  5 :
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7]

根据上网时长聚类

import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
import matplotlib.pyplot as plt

mac2id = dict()
online_times = []
f = open('E:/Anaconda/DATA/TestData.txt', 'r')
for line in f:

    # 读取每条数据中的mac地址，
    # 开始上网时间，上网时长

    mac = line.split(',')[2]
    online_time = int(line.split(',')[6])
    start_time = int(line.split(',')[4].split(' ')[1].split(':')[0])

    # mac2id是一个字典：
    # key是mac地址
    # value是对应mac地址的上网时长以及开始上网时间（精度为小时）

    if mac not in mac2id:
        mac2id[mac] = len(online_times)
        online_times.append((start_time, online_time))
    else:
        online_times[mac2id[mac]] = [(start_time, online_time)]

# -1:根据元素的个数自动计算此轴的长度
# X：上网时间
real_X = np.array(online_times).reshape((-1, 2))
X = np.log(1 + real_X[:, 1:])

# 调用DBSCAN方法进行训练 ，
# labels为每个数据的簇标签

db = skc.DBSCAN(eps=0.14, min_samples=10).fit(X)
labels = db.labels_

print('Lables:')
print(labels)
raito = len(labels[labels[:] == -1]) / len(labels)
print('Noise raito:', format(raito, '.2%'))

# Number of cluster in lables, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)

print('Estimated number of clusters: %d' % n_clusters_)
print('Silhouette Coefficient: %0.3f' % metrics.silhouette_score(X, labels))

# 统计每一个簇内的样本个数 ， 均值，标准差

for i in range(n_clusters_):
    print('Cluster ', i, ':')
    count = len(X[labels == i])
    mean = np.mean(real_X[labels == i][:, 1])
    std = np.std(real_X[labels == i][:, 1])
    print('\t number of sample: ', count)
    print('\t mean of sample  : ', format(mean, '.1f'))
    print('\t std of sample   : ', format(std, '.1f'))

输出

Lables:
[ 0  1  0  4  1  2  0  2  0  3 -1  0 -1 -1  0  3  1  0  3  2  2  1  2  0  1
  1 -1 -1  0  0  0  0  1  0 -1  0  0  0  2  0  1  0 -1 -1  0  0  0  3  2  0
 -1  1  0  1  0  0 -1  2  0  0  0  1  3  3  0  2  0 -1  3  0  0  2  0  0  0
  2  1 -1  0  0  0  0  0  0  1 -1  0  3  1  0  1  1  0  1  0  1  0  0 -1  1
  1  0  0  2  0  0  0  2  2  0  0  0 -1  0  0  4  0  1  2 -1  0  1  0  2  0
 -1 -1 -1  0  1  1  3 -1  0  1  0  2  0  0  2  1  1  0  0  0  0  4 -1  0  0
  0  0  2  0  0  0  0 -1  2  0  0  0  0  4  0  0 -1  0  2  0  0 -1  0  1  4
  0  0 -1  1  1  0  0  2  0  0  3 -1 -1 -1  1  0  0  2  1  0 -1 -1  3  2  2
  0  0  3  0  1  0  0  0  3  2  0 -1  0  1 -1 -1  0  2  2  1  4  0  0  1  0
  2  0  0  0  0  1  1  0  0  1  0  4 -1 -1  0  0  0 -1 -1  1 -1  4 -1  0  2
  2 -1  2  1  2 -1  0 -1  0  2  2  1 -1  0  1  2 -1 -1  1 -1  2 -1 -1  1  4
  2  3  1  0  4  0  0  4  2  4  0  0  2 -1]
Noise raito: 16.96%
Estimated number of clusters: 5
Silhouette Coefficient: 0.227
Cluster  0 :
         number of sample:  128
         mean of sample  :  5864.3
         std of sample   :  3498.1
Cluster  1 :
         number of sample:  46
         mean of sample  :  36835.1
         std of sample   :  11314.1
Cluster  2 :
         number of sample:  40
         mean of sample  :  843.2
         std of sample   :  242.9
Cluster  3 :
         number of sample:  14
         mean of sample  :  16581.6
         std of sample   :  1186.7
Cluster  4 :
         number of sample:  12
         mean of sample  :  338.4
         std of sample   :  31.9