R语言非线性方程组求解dfsane,nleqslv
首先,dfsane属于BB包,使用时应首先载入library("BB")
nleqslv 属于nleqslve包,同样使用时应载入 library("nleqslve")
Description
Derivative-Free Spectral Approach for solving nonlinear systems of equations
求解非线性方程组法
Usage
dfsane(par, fn, method=2, control=list(),
quiet=FALSE, alertConvergence=TRUE, ...)
library(BB)
fun <- function(x) {
f <- numeric(length(x))
f[1] <- x[1]/(1+exp(x[2]*0.215+x[3]))-134.03
f[2] <- x[1]/(1+exp(x[2]*5.06+x[3]))-80.2
f[3] <- x[1]/(1+exp(x[2]*9.85+x[3]))-13.4
f
}
startx <- c(132,0.5,0.5)
result = dfsane(startx,fun,control=list(maxit=2500,trace = FALSE))
theta = result$par
fun函数就是 fn,公式中第二个,你的非线性方程组的公式比如,在本例中 y = a/(1+exp(bx+c)
在本方程中x,y为已知坐标点,求a,b,c的值
在fun中,参数只为x,此x并非自变量x,而是一个list,也就是向量即你要求的参数值(a,b,c的值)的表示,也即用dfsane的求得的解,x[1]表示a,x[2]表示b,x[3]表示c。
由于0 = a/(1+exp(bx+c) - y, 所以即求 f = a/(1+exp(bx+c) - y由于要求a,b,c,在原方程中x,y已知,带入。
求解三个参数最少需要三个方程组联立,f[1],f[2],f[3]即为三个数组联立,用dfsane求解,求得的解即为要求a,b,c的值
control=list(maxit=2500,trace = FALSE),maxit搜索的迭代次数,一般100,200,trace默认值为true,把每一步迭代的结果都给列出事,事实上,我们用不到知道每一步的解,只要一个最终结果就行了,所以设置为false, control 里一般使用这两个参数
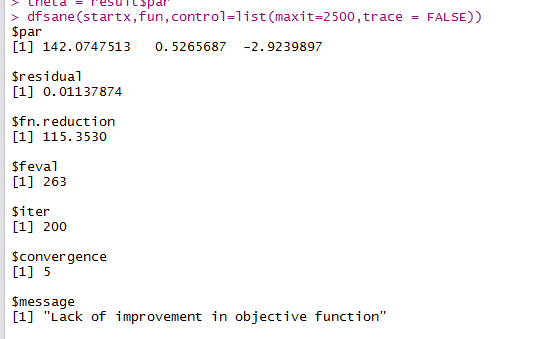
运行结果:
par就是要求的a,b,c的解,即为向量(list)x的值,可以用如下获取:
result = dfsane(startx,fun,control=list(maxit=2500,trace = FALSE))
theta = result$partheta即为向量x的值
在此例中a = theta[1],b= theta[2],c=theta[3]
http://www.inside-r.org/packages/cran/bb/docs/dfsane 点击打开链接
再来一个例子
#y ~ a +(b*exp(c*x^d))
tempFunction1 <- function(modelParams){
F = numeric(length(modelParams))
F[1] = modelParams[1]+(modelParams[2]*exp(modelParams[3]*(exp(2.751514))^modelParams[4])) - 107.20561
F[2] = modelParams[1]+(modelParams[2]*exp(modelParams[3]*(exp(5.509109))^modelParams[4])) - 70.53738
F[3] = modelParams[1]+(modelParams[2]*exp(modelParams[3]*(exp(6.779219))^modelParams[4])) - 42.44393
F[4] = modelParams[1]+(modelParams[2]*exp(modelParams[3]*(exp(8.542089))^modelParams[4])) - 17.10280
F
}
theta = dfsane(par= c(100 + 50*runif(1),runif(1),-runif(1),runif(1)), fn=tempFunction1,control = list(maxit = 2500,trace = FALSE))
theta$par
#那么a = theta$par[1] b = theta$par[2] c = theta$par[3] d= theta$par[4] 博主微博:文二十口