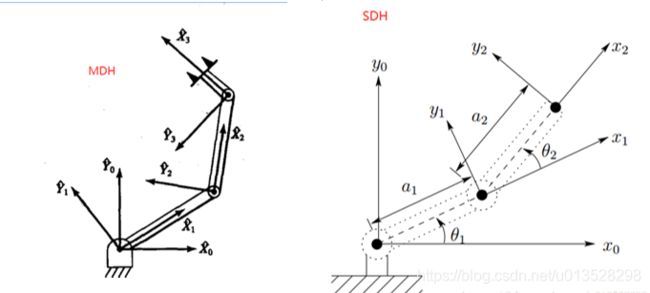
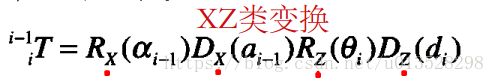建立DH模型的三种方法以及区别

目录

1.建立DH模型的三种方法

2.SDH和MDH的应用范围

3. SDH和MDH的区别

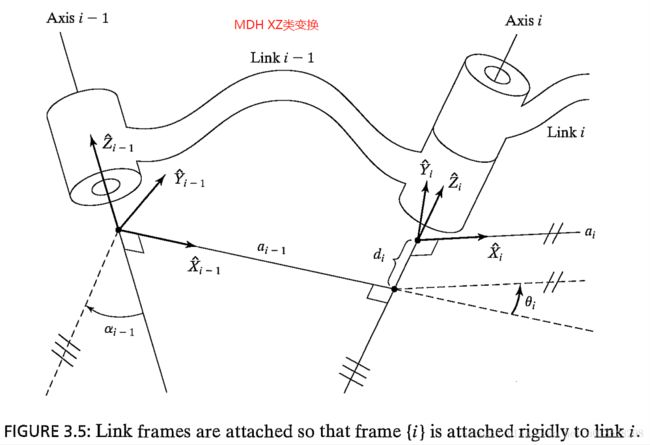
0.SDH是ZX类变换，MDH是XZ类变换 

1.SDH和MDH都是强调把坐标系建立在连杆上

2.举个例子说明SDH和MDH的区别

2.1SDD和MDH的dh条件

2.2举一个XZ变换的例子

2.3mdh和sdh都有0坐标系区别是什么

3.ZX变换和XZ类变换事实上是等价的

---

 

1.建立DH模型的三种方法

       6R工业机器人系统本质上是一种半闭环的控制结构， 系统只能精确控制关节伺服电机位置， 而电机位置与机器人末端执行器位姿之间关系通过运动学确定。 理论运动学模型与实际模型之间不可避免存在误差， 因此需要通过标定提高机器人的绝对位置精度。

        根据旋转顺序的不同将 24 种变换分成（1）（2）两类各 12 种：

（1） 先绕 Z 轴旋转，再绕 X 轴旋转（例如Spong书中的DH方法）
（2） 先绕 X 轴旋转，再绕 Z 轴旋转（例如Craig书中的DH方法）

          为方便描述， 称第一种为 ZX 类变换，第二种为 XZ 类变换。

虽然有点不准确，但是为了随大流，我们把Spong书中的DH方法叫做SDH，Craig书中的DH方法叫做MDH（个人认为增加了第五个参数的DH方法才能叫做MDH，不然的话应该是算做DH参数ZX变换或者XZ变换）

 

  (3)   在描述机器人的绝对定位误差模型时 ,传统的DH模型在相邻两关节轴线平行时 ,平行度的微小偏差将导致实际公法线的位置与理论公法线的位置存在极大偏差。因此 ,需要增加绕 Y 轴的转动项 ,即扭角Ui。当相邻关节轴线平行时扭角Ui 的值定义为零 。

补充：

(1)激光跟踪仪的作用：利用激光跟踪仪确定机器人的基坐标系并测量机器人绝对位置 

2.SDH和MDH的应用范围

 SDH模型是针对serial structure的机器人的。当用SDH模型来处理tree structure robot或者closed loop structure robot 的时候会产生歧义。MDH模型可以用统一的定义来处理serials structure, tree stucture, closed loop structure，甚至mobile robots.

3. SDH和MDH的区别

                   

0.SDH是ZX类变换，MDH是XZ类变换 

ZX类变换：一开始绕着i-1坐标系的的Zi-1轴旋转和平移，然后就到了X轴的旋转和平移，但这时是相对i坐标系的Xi轴进行旋转和平移。（也就是到了下一个坐标系，从i-1到i）

XZ类变换：与ZX类变换类似，就不赘述了       

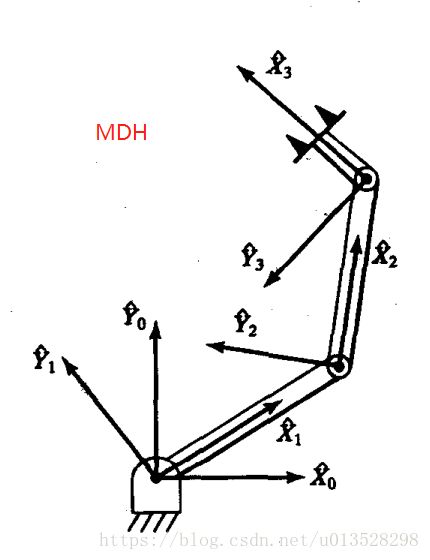
1.SDH和MDH都是强调把坐标系建立在连杆上

 sdh关节i上安装的是i-1坐标系，管的是连杆i-1(即连杆i-1上的点在i-1坐标系里表示)  ，即坐标系建在连杆的尾端                   

 mdh关节i上安装的是i坐标系，管的是连杆i (即连杆i上的点在i坐标系里表示)，即坐标系建在连杆的首端

2.举个例子说明SDH和MDH的区别

注：比如说a1，sdh方法是0坐标系到1坐标系的转换获得的，mdh方法是1坐标系到2坐标系的转换获得的。

(a) 

   

SDH的0坐标系和1坐标系 不重合，1坐标系绕着Z0转动 

因为0坐标系和1坐标系不重合 ，第一个连杆总是有长度的。

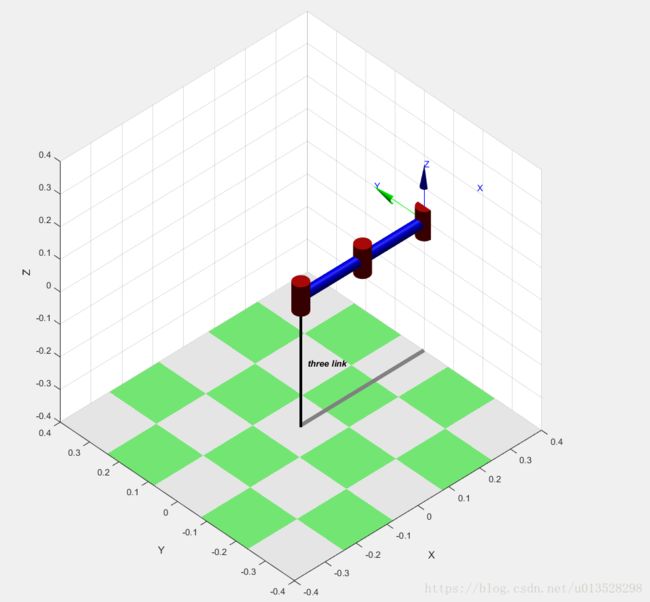
 使用matlab工具箱建模：

%2.创建一个具有n个自由度的机械臂  sdh
L(1)=Link('revolute', 'd',0, 'a', 1, 'alpha', 0);
L(2)=Link('revolute', 'd', 0, 'a', 0.8, 'alpha', 0);
 %3.通过构造函数给创建的机械臂对象命名，并显示出对象的信息
two_link=SerialLink(L,'name','two link')
%机器人正运动学
%1.数组中的参数是每一个关节的角度
% 获得的是坐标系N相对于坐标系0 的变换矩阵
two_link.fkine([0 0]);%获得的是T30变换矩阵
%2.将创建的机械臂可视化 数组中的参数是每一个关节的角度
two_link.plot([0 0 ])
 

可视化： 

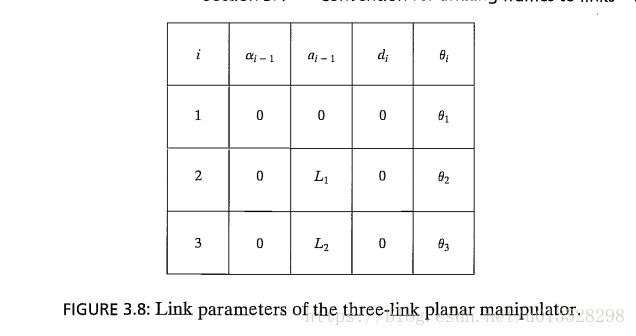
使用matlab工具箱建模(为了和下文对比建立的是3连杆机械臂) ：

%2.创建一个具有n个自由度的机械臂  sdh
L(1)=Link('revolute', 'd',0, 'a', 1, 'alpha', 0);
L(2)=Link('revolute', 'd', 0, 'a', 0.8, 'alpha', 0);
L(3)=Link('revolute', 'd', 0, 'a', 1, 'alpha', 0);
%3.通过构造函数给创建的机械臂对象命名，并显示出对象的信息
three_link=SerialLink(L,'name','three link')
%机器人正运动学
%1.数组中的参数是每一个关节的角度
% 获得的是坐标系N相对于坐标系0 的变换矩阵
three_link.fkine([0 0 0]);%获得的是T30变换矩阵
%2.将创建的机械臂可视化 数组中的参数是每一个关节的角度
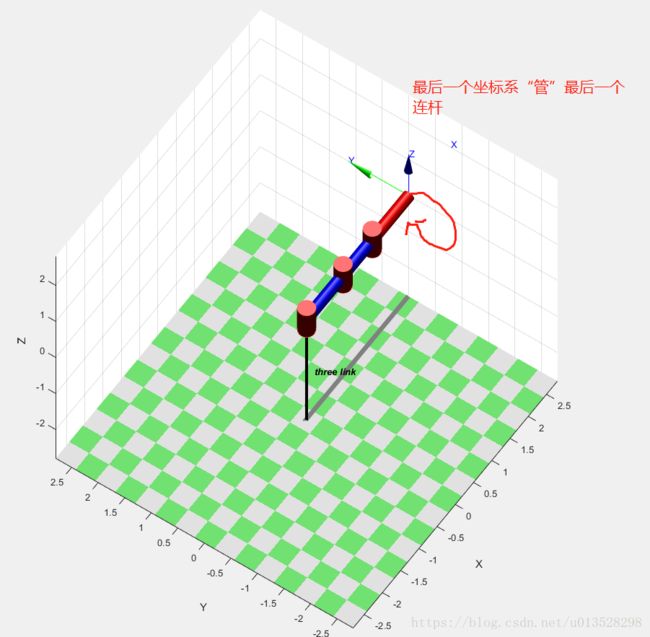
three_link.plot([0 0 0])

 可视化：

 

(b) 

            

    

                                                                    

  MDH的0坐标系和1坐标系 重合，1坐标系绕着Z1转动标题

      因为0坐标系和1坐标系重合，所以连杆0的长度总是0。 

                                                         

使用matlab工具箱建模 ：

%2.创建一个具有n个自由度的机械臂  使用mdh
L(1)=Link('revolute', 'd',0, 'a',0, 'alpha', 0,'modified');
L(2)=Link('revolute', 'd', 0, 'a', 0.2, 'alpha', 0,'modified');
L(3)=Link('revolute', 'd', 0, 'a', 0.2, 'alpha', 0,'modified');
%3.通过构造函数给创建的机械臂对象命名，并显示出对象的信息
three_link=SerialLink(L,'name','three link');
%4.获得创建的机械臂的各种参数
 three_link.n
%获得正运动学 
%1.数组中的参数是每一个关节的角度
% 获得的是坐标系N相对于坐标系0 的变换矩阵
three_link.fkine([0 0 0]);%获得的是T30变换矩阵
%2.将创建的机械臂可视化 数组中的参数是每一个关节的角度
three_link.plot([0 0 0])

可视化：

MDH

 

 

2.1SDD和MDH的dh条件

SDH：Xi和Zi-1垂直且相交                   MDH:Xi和Zi+1垂直且相交

（其实这就是连杆的坐标系是建在头部还是尾部造成的）

2.2举一个XZ变换的例子

                                                   

                                                                      

由图可以假设一个机械臂上已经固定好了坐标系，那么关节i-1上的坐标系i-1怎么通过旋转和平移转换到i坐标系上呢？

首先绕着Xi-1轴旋转使Zi-1轴和Zi轴平行，然后再沿Xi-1轴平行ai-1，此时i-1坐标系的原点和i坐标系的原点重合。

此时再进行旋转和平移就是针对i坐标系进行了，绕着Zi坐标系旋转，然后沿着Zi平移di，这时，i-1坐标系就和i坐标系完全重合了。

2.3mdh和sdh都有0坐标系区别是什么

仍然以二连杆举例

mdh：

0坐标系不动，1坐标系建立在首端，theta1是1坐标系的x轴和0坐标系的x轴之间的夹角。

sdh：

0坐标系不动，1坐标系建立在尾端，theta1是1坐标系的x轴和0坐标系的x轴之间的夹角。

 

3.ZX变换和XZ类变换事实上是等价的

                                    

欧几里得空间中，仅包含平移和旋转变换时的坐标系变换顺序定理：
定理 1： 在连续变换条件下，任意平移的顺序可互换；
定理 2： 在连续变换条件下，同一轴的旋转和平移顺序可互换。

所以我们可以得知二者是等价的.

 

4.坐标系的建立和DH参数并不是唯一的参考craig的书英文版P74

5.craig的书中第75页，关于针对每一个建立中间坐标系的思考方法非常漂亮，可以认真体会一下。

6.在现实中建立机器人模型的时候有的坐标系需要考虑零位，比如可能在零位的时候X1和X2是垂直的，那么绕着Z1轴的旋转角就是90+ θ2.

参考：

1.自己的手写笔记

2.Introduction to Robotics Mechanics and Control  John J.Craig

3.基于 DH 参数的机器人建模中几个要点的讨论和提出一种新的修正模型 李少珂