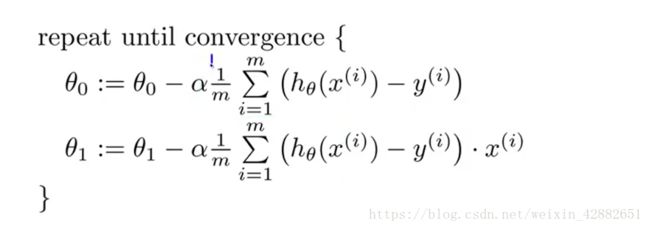初识：梯度下降算法 (Gradient Descent) ----直线拟合散点

我的第一个机器学习算法。

---

梯度下降算法解决散点拟合问题：
在直角坐标系中给出若干个点作为训练集(Training Set),使用梯度下降算法给出最合适的拟合直线。

---

1.大体思路(我个人的理解)：
对于许多散步在直角坐标系中的点，首先给出一个初始的拟合直线( 例如y=0*x+0)。然后在算出这条直线与训练集中的个点的距离差值的和的平方(误差函数 J(x1,x2) )。这里设拟合直线方程为y=x1 * x + x2。(x1,x2为变量)。然后对这个误差函数J(x1,x2)使用梯度下降算法求得当J(x1,x2)最小时，x1 x2的取值。进而就得到了最优的拟合直线 y= x1 * x + x2

---

梯度下降算法的大致思想：
对于一个函数J(x)，下式：x = x - (alpha) * ( J(x)' ) (这里的 ’ 是指导数)就是对于J(x)的梯度下降算法。
首先给x指定一个初值 x0
(1) 当在x0 处J(x)导数值为负：x就会增加
(2) 当在x0 处J(x)导数值为正：x就会减小
因此x会不断向J(x)的最低处所对应的x值偏移。

alpha 是一个参数，称为学习速率,它控制了x增大或减小的速度，也可以理解为每一步x走的距离。
(1)alpha过大时，可能会直接跳过最优点，从而得不到最优解，甚至逐渐发散。
(2)alpha过小时，则可能因为步子过小而经过很多次改变才得到最优解，消耗过多的资源。它的最好取值可能因数据不同而不同，还需要在程序中不断改变探索。

经过有限次的改变，x最终可以变为使J(x) 最小的值。

---

从而对于y=x1 * x + x2这样有两个变量的函数。只需要同时对x1 和 x2 进行梯度下降算法的处理，直到 x1 x2 均变为能使J(x1,x2)最小化的值即可得到最优的拟合直线。

那么要同时对x1 x2 进行梯度下降算法的处理，首先要保证它们同时参与 J(x1,x2) 的计算，又要保证它们各自梯度变化的独立性。
那么应当：
(1) 设定x1 x2 初值
(2)J(x1,x2)分别对x1 x2求偏导，分别得到x1与x2的误差函数J(x)
(3) 对x1 x2误差函数进行梯度下降
(4)检查x1与x2是否都达到了最优值，若否则返回(3)
(5)得到了最优拟合 y = x1 * x + x2

---

2.程序实现(C++)：
(1)给出训练集(散点集)，学习速率 αlpha

 //set_x与set_y 分别存储x,y 轴的坐标
double Train_set_x[17] = { 1.1, 2.4, 2.4, 3.1, 2.2, 4.42, 5.43, 4.5, 5.28, 7.35, 10, 8.27, 12.6, 12.8, 9.69, 15.0, 13.69 };
double Train_set_y[17] = { 2.5, 1.7, 3, 4.0, 5.2, 6.53, 7.33, 8.7, 4.2, 5.8, 6.05, 8.05, 7.41, 8.89, 10.12, 9.72, 10.83 };
double m = 17.00;       //共有17个点
double alpha = 0.0001;

(2)定义好过程中需要的变量

    double temp_1=0;     //用于更新x1的值
    double temp_2=0;     //用于更新x1的值
    double sum_1, sum_2;
    double x1 = 0;   // y=x1*x+x2  为所拟合出来的函数 先将x1 x2初始化为0
    double x2 = 0;

(3)进行梯度下降：

//为了防止alpha过大而导致的发散，这里循环里放了一个很大的数来限制，比如999999999,避免陷入死循环

for (i = 1;i<999999999 ; i++)   //符合跳出条件后，会 break跳出,i可以提示最后进行了多少次变化
    {
        sum_1 = 0;
        sum_2 = 0;  
        for (int j = 0; j <= 16; j++)  //进行求和操作
        {
            sum_1 += x2 + x1*Train_set_x[j] - Train_set_y[j];   //这里是J(x1,x2)对x2的偏导
        }
        for (int m = 0; m <= 16; m++)
        {
            sum_2 += (x2 + x1*Train_set_x[m] - Train_set_y[m])*Train_set_x[m];   //这里是J(x1,x2)对x1的偏导

        }

        temp_1 = x2 - alpha*(1 / m)*sum_1;   //梯度下降
        temp_2 = x1 - alpha*(1 / m)*sum_2;

---

这里取的标准是这个：
θ0即为x2 θ1即为x1
这里的表述应该是： y = θ1 * x + θ0

---

这里我大概写了个推导，应该是这样子的：

---

(4)检验是否为最优解：

if ( (temp_1==x2) && (temp_2 ==x1))  //若x1 x2都不再改变，即都已经收敛到了最优处，就可以退出循环，得到最优解
        {

            break;
        }

（5）若为达到最优解的条件，则更新x1 x2的值，进行下一次循环

        x2 = temp_1;   
        x1 = temp_2;

---

以下是完整的程序代码：

#include
#include

using std::cout;
using std::cin;
using std::endl;

 //set_a与set_b 分别存储x,y 轴的坐标
double Train_set_x[17] = { 1.1, 2.4, 2.4, 3.1, 2.2, 4.42, 5.43, 4.5, 5.28, 7.35, 10, 8.27, 12.6, 12.8, 9.69, 15.0, 13.69 };
double Train_set_y[17] = { 2.5, 1.7, 3, 4.0, 5.2, 6.53, 7.33, 8.7, 4.2, 5.8, 6.05, 8.05, 7.41, 8.89, 10.12, 9.72, 10.83 };
double m = 17.00;       //共有17个点

double m = 17.00;
double alpha = 0.001;


int main()
{
    int i ;
    double temp_1=0;
    double temp_2=0;
    double sum_1, sum_2;
    double x1 = 0;   // y=x1*x+x2  为所拟合出来的函数 先将x1 x2初始化为0
    double x2 = 0;


    for (i = 1; ; i++)   //符合跳出条件后，会break跳出
    {
        sum_1 = 0;
        sum_2 = 0;  
        for (int j = 0; j <= 9; j++)
        {
            sum_1 += x2 + x1*Train_set_a[j] - Train_set_b[j];
        }
        for (int m = 0; m <= 9; m++)
        {
            sum_2 += (x2 + x1*Train_set_a[m] - Train_set_b[m])*Train_set_a[m];
        }

        temp_1 = x2 - alpha*(1 / m)*sum_1;
        temp_2 = x1 - alpha*(1 / m)*sum_2;

        if ( (temp_1==x2) && (temp_2 ==x1))
        {

            break;
        }

        x2 = temp_1;
        x1 = temp_2;


    }
    if ((x2 < 0.0001) && (x2>-0.0001)) x2 = 0;

    cout << "拟合的结果为：  y=" << x1 << "x+" << x2 << endl;
    cout << "进行了" << i << "次" << endl;

    system("pause");

    return 0;
}

运行结果：

在纸上画了一下，还真没什么好挑剔的 :)