MATLAB强化学习入门——四、用DQN实现网格迷宫算例

上期我们聊了两个小问题，第一是为什么需要深度Q学习，第二则是MatLab神经网络工具箱的使用。那么本期，我们就尝试将DQN移植到第二期我们完成的Q-Learning网格迷宫程序中，尝试深度Q学习的算例实现。

一、Deep-Q-Network算法核心

总的来说，DQN的核心思想就是使用一个深度神经网络模型代替Q表来实现智能体对状态的估计。那么，这种替代就需要实现以下几个核心的功能：

1. 在Q-Learning中，智能体以‘状态-动作对’为索引在Q表中获得对该状态-动作对的价值估计——Q函数值。对应的，在DQN中，我们希望神经网络能以状态-动作对为输入，以Q函数值为输出。
2. 之所以Q-Learning、Sarsa等算法最终能够得到对状态的准确估计，原因在于这些算法在智能体运动时始终对Q函数表进行迭代。在DQN中，我们采用类似的思想，利用下一状态和奖赏获得目标Q值(Q_target)，与神经网络当前得到的Q值(Q_eval)进行比较；随后将两者的误差通过梯度下降法反向传播回神经网络中，从而实现Q-Network的训练与更新。

而为了实现Q-Network准确而高效的训练与更新，DQN算法的迭代策略展现出了两个重要区别：记忆重现(Replay Memory)与固定目标网络(Fixed Q Target)。
记忆重现是指：不同于Q-Learning里智能体会在每行动一步后即对对应Q值进行更新，我们将智能体所经历的状态、动作、次状态均记录在一个记忆回放的存储区内，间隔一定的运动步数方才更新神经网络。更新神经网络时，从ReplayMemory中取一定量的‘状态-动作-次状态对’计算次状态的最大Q值以及回报，从而得到对应目标Q值(Q_target)。最后将这一批(batch)数据统一输入神经网络中进行训练。由于ReplayMemory是独立于神经网络的存在，这保证了训练数据的相对独立性。也因此，一方面，神经网络模型不会在训练时因为最近几次可能的错误尝试而“练偏”；另一方面，我们甚至可以在ReplayMemory中添加筛选好的或者其它智能体的训练数据来训练当前神经网络。
固定目标网络则将Q-Network构成的“Q表”分成了两份，一份在智能体选择动作时使用，另一份则在智能体计算Q_target的时候使用。在程序初始化的时候，计算Q_target的目标网络与选择动作的评估网络是一致的。然而随后，目标网络的更新将滞后于评估网络：评估网络每更新数次，我们才将评估网络的参数赋给目标网络，实现目标网络的更新。从理论上将，这一方法能够提高算法的稳定性。
下图即用伪代码的形式展示了算法从Q-Learning变化至Deep-Q-Network的主要变更。变化主要体现在三部分，分别是：①神经网络模型及对应结构的初始化，②利用神经网络选择动作，③存储状态等信息并训练更新神经网络。

下图即用伪代码的形式展示了算法从Q-Learning变化至Deep-Q-Network的主要变更。变化主要体现在三部分，分别是：①神经网络模型及对应结构的初始化，②利用神经网络选择动作，③存储状态等信息并训练更新神经网络。

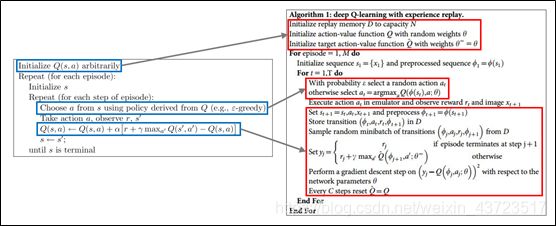
图1 DQN算法与Q-Learning算法的主要差异

而上图算法中没能展现出来的，还有DQN的另一个要点，就是DQN训练的分期。DQN的训练是依赖数据的，而程序初始化以后显然没有能够供DQN进行训练的数据。因此，我们在训练期之前需要设置一个观察期。在观察期内，智能体仅执行动作，不训练网络。从而在训练期初期，有足够的数据供神经网络训练。

二、 网格迷宫MatLab程序实现

在对算法有了足够的了解后，我们即可用流程图来分析网格迷宫算例的实现。我们将程序拆分为三个主要的执行阶段，分别是参数的初始化、观察期的执行与训练期的执行。

图2 DQN网格迷宫流程图

2.1 程序初始化

参数初始化阶段，我们需要完成环境参数、智能体参数、训练记录和动态绘图的初始化。首先是网格迷宫的有关参数，这些参数与Q-Learning算例中的参数是在形式上是一致的。然而既然使用了神经网络模型，我们不妨将迷宫的规模扩大一些，变为60×35的。另外，我们将迷宫大小等重要常参数设置为全局变量，以方便不同函数之间的调用。
随后我们使用fitnet()生成一个共两层，每层40个神经元的初始化神经网络。从这里我们可以看到，由于算例简单，我们实际上并不需要复杂的多层的神经网络来进行计算，简单的神经网络也能够满足运算。在该算例下，实际上并不存在DQN，而仅仅是Q-Network，随后的倒立摆问题亦是如此。虽然DQN在实际的设计过程中不仅需要优化神经网络结构，还需要详细考虑训练方式以提高效率，但其算法的核心思想与本篇所讨论的内容是几乎一致的。这也是为什么，在笔者所学习的资料以及本文中，使用的是一种非深度神经网络去讨论DQN的算法并实现算例。
在初始化神经网络后，我们还需要定义一个数据集训练神经网络以规定其输入和输出。最后将训练方法设计为梯度下降法，并关闭训练图窗（不停的跳出来实在是有点儿烦）。
初始化阶段最后的任务是生成动态绘图需要的数据结构并调用动态绘图指令，原因在于，在MatLab中，调用神经网络执行算例后，计算时间大大增加。我们没必要等到10000次训练结束后再分析结果，而可以用动态绘图的方式在程序运行的过程中即对程序是否编写正确进行判断。

clear all;
%定义全局参数，方便函数调用
global Gwidth Gheight N_act targetxy gamma;

%网格迷宫参数
Gwidth=60;
Gheight=35;
N_act=4;
%风速初始化
Windyworld.windx=zeros(Gheight,Gwidth);
Windyworld.windy=zeros(Gheight,Gwidth);
Windyworld.windy(:,6:9)=Windyworld.windy(:,6:9)+1;   %%Windyworld.windy(:,7:8)=Windyworld.windy(:,7:8)+1;
targetxy=[10,14];                 %!!注意：第一个坐标为y坐标，第二个坐标为x坐标 
startxy=[1,4];
step=1;

%时间设置：观察期，训练期
T_obs=500;                      
T_train=10000;
T_episode=200;

%DQN神经网络初始化
QNet_eval=fitnet([40,40]);
Iniset=zeros(4,400);  %前三行为输入，最后一行为目标输出
for i=1:40
    Iniset(1,i)=unidrnd(Gheight);
    Iniset(2,i)=unidrnd(Gwidth);
    Iniset(3,i)=unidrnd(N_act);
    if Iniset(3,i)==1
        Iniset(4,i)=0.2;
    
    else if Iniset(3,i)==2
            Iniset(4,i)=-0.2;
        end
        %}
    end
end
clear i;
QNet_eval=train(QNet_eval,Iniset(1:3,:),Iniset(4,:));
QNet_target=QNet_eval;
%将神经网络训练算法设置为自适应动量梯度下降法
QNet_eval.trainFcn='traingdx';  
%关闭训练图窗nntraintool
QNet_eval.trainParam.showWindow=0;


%Replaymemory初始化：
S_memo=8000;
Rmemo=zeros(5,S_memo);    %1:2：rolexy,3：act,4:5：nextxy
Memopointer=1;  %Replay memory的写入指针

%学习参数初始化
gamma=0.99;      
nBatch=400;
T_gap=400;   %20,25,30
T_renew=3*T_gap;

%记录列表初始化
Successmark=zeros(1,T_obs+T_train);
AveSuccess=zeros(1,T_obs+T_train);
TotalSuccess=zeros(1,T_obs+T_train);

%动态绘图初始化
Plotset=zeros(2,1);
p = plot(Plotset(1,:),Plotset(2,:),...
   'EraseMode','background','MarkerSize',5);
axis([0 T_obs+T_train 0 1]);

2.2 观察期与训练期：优化执行效率

观察期和训练的代码几乎一致，区别仅在于训练神经网络的部分。**在第三期里，我们讨论过神经网络调用效率的问题。简而言之，在MatLab中，调用神经网络400次计算400个输入的耗时将远高于一次使用神经网络计算400个输入。**在网格迷宫里，我们需要在两个地方调用神经网络，第一是在tcegreedy()函数中选择动作，第二是在获得次状态后计算Q_target.
在tcegreedy()函数中，我们需要计算当前状态下4个动作的Q值并选择其中Q值最大的动作作为输出。在tcegreedy()内部，我们需要将4个动作的输入拼接起来一次性输入神经网络中以提高效率；而在tcegreedy()外部，由于智能体执行动作并与环境交互的顺序性不能改变，我们只能一次次调用tcegreedy()而没法再提高调用效率了。
然而，计算Q_target的过程存在大幅提高调用效率的可能。由于神经网络的训练是存在间隔和采样批次的，我们没必要在每获得一个新状态后就立刻计算Q_target，而可以在ReplayMemory中记录‘状态-动作-次状态对’。在训练前从ReplayMemory中采样，一次性输入到QNet中获得次状态Q值以计算Q_target。这就是函数CalculationQtarget()的由来。

%观察期：此期间不更新Qnet,仅记录replay memory
for Ts=1:T_obs
    rolexy=startxy;
    %result(Ts).trace=zeros(40,3);
    %result(Ts).trace(1,:)=([1,rolexy(1),rolexy(2)]);
    for Tm=1:T_episode
      %根据tcegreedy策略执行动作
        [act,Q_now]=tcegreedy(Ts,rolexy,QNet_eval);
        nextxy=movement(act,rolexy,Windyworld);
      %Replaymemory记录+指针更新
        Rmemo(:,Memopointer)=[rolexy';act;nextxy'];
        Memopointer=PointerMove(Memopointer,S_memo);
      %更新位置
        step=step+1;
        rolexy=nextxy;
        %result(Ts).trace(Tm+1,:)=([Tm+1,rolexy(1),rolexy(2)]);
            %判断是否跳出本episode
        if rolexy(1)==targetxy(1)&&rolexy(2)==targetxy(2)
            Successmark(Ts)=1;
            break;
        else if rolexy(1)<1||rolexy(1)>Gheight||rolexy(2)<1||rolexy(2)>Gwidth
                break;
            end
        end    
    end
    %数据记录
    TotalSuccess(Ts)=sum(Successmark(1:Ts));
    AveSuccess(Ts)=TotalSuccess(Ts)/Ts;
    %动态绘图
    if mod(Ts,10)==0
        TempP=[Ts;AveSuccess(Ts)];
        Plotset=[Plotset,TempP];
        set(p,'XData',Plotset(1,:),'YData',Plotset(2,:));
        drawnow
        axis([0 T_obs+T_train 0 1]);             
    end
end

%探索期
%探索期开始更新神经网络参数
Tnode1=1+T_obs;
Tnode2=T_obs+T_train;
%网络训练参数更新
for Ts=Tnode1:Tnode2
    rolexy=startxy;
    %result(Ts).trace=zeros(40,3);
    %result(Ts).trace(1,:)=([1,rolexy(1),rolexy(2)]);
    for Tm=1:T_episode
      %根据tcegreedy策略执行动作
        [act,Q_now]=tcegreedy(Ts,rolexy,QNet_eval);
        nextxy=movement(act,rolexy,Windyworld);
      %为提高效率，Q_target统一在训练神经网络时更新
      %Replaymemory记录+指针更新
        Rmemo(:,Memopointer)=[rolexy';act;nextxy'];
        Memopointer=PointerMove(Memopointer,S_memo);
      %更新位置
        step=step+1;
        rolexy=nextxy;
        %result(Ts).trace(Tm+1,:)=([Tm+1,rolexy(1),rolexy(2)]);
        %判断是否跳出本episode
        if rolexy(1)==targetxy(1)&&rolexy(2)==targetxy(2)
            Successmark(Ts)=1;
            break;
        else if rolexy(1)<1||rolexy(1)>Gheight||rolexy(2)<1||rolexy(2)>Gwidth
                break;
            end
        end
        
      %按照T-renew间隔更新估计Q_target的目标神经网络QNet_target  
       if mod(step,T_renew)==0
           QNet_target=QNet_eval;
       end
       
       %按照T_gap的间隔训练估计Q_eval的评估神经网络QNet_eval
       if mod(step,T_gap)==0
           %1. 利用Rmemo生成训练数据级
           Trainset=zeros(6,nBatch);  %前五行与replaymemory一致，后一行为利用QNet_target计算得到的Q_target
           i=1;
           while i<=nBatch
               num1=unidrnd(S_memo);  %随机抽取ReplayMemory中的数据
               if Rmemo(1,num1)>0
                   Trainset(1:5,i)=Rmemo(:,num1);
                   i=i+1;
               end
           end
           %2. 计算Q_target
           Trainset(6,:)=CalculationQtarget(Trainset(1:5,:),QNet_target);
           %3. 训练QNet_eval
           QNet_eval=train(QNet_eval,Trainset(1:3,:),Trainset(6,:));
       end
    end    

    %数据记录
    TotalSuccess(Ts)=sum(Successmark(1:Ts));
    AveSuccess(Ts)=TotalSuccess(Ts)/Ts;
    %动态绘图
    if mod(Ts,10)==0
        TempP=[Ts;AveSuccess(Ts)];
        Plotset=[Plotset,TempP];
        set(p,'XData',Plotset(1,:),'YData',Plotset(2,:));
        drawnow
        axis([0 T_obs+T_train 0 1]);             
    end
end

2.3 Let it RUN

以上，我们就介绍了在MATLAB中使用DQN算法实现网格迷宫算例的编程要点。
Let it run and show the result.
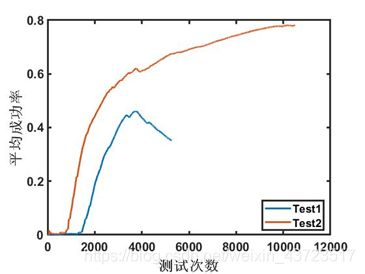我们展示DQN两个训练周期里的表现，Test1中，训练到3000左右时，智能体的表现突然下滑，这可能是神经网络过拟合造成的，也可能是不良训练样本训练造成的影响。Test2则表现出了较为正常的训练情况，曲线也与Q_Learning类似。

以上，我们就讨论完了《MatLab强化学习入门》第四期的所有内容。完整的代码包将以资源的形式上传。

十分欢迎有心读本文的CSDNer交流讨论；如果觉得本文有帮助的话，打赏一下可是更好(๑•̀ㅂ•́)و✧