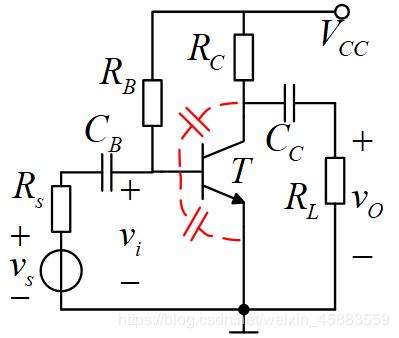
小信号放大电路的频率特性
小信号放大电路的频率特性
- 频率特性概述
- 频率特性基本概念
- 频率特性分析基本方法
- 多级放大电路增益的频率特性.
- 晶体管结电容对高频特性的影响
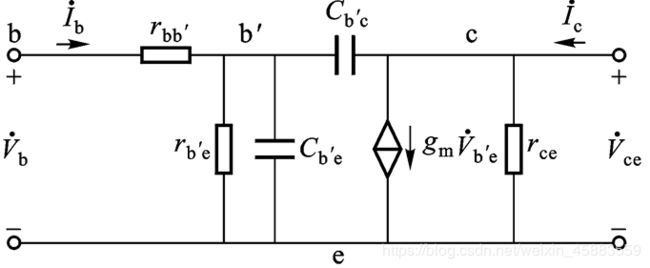
- 高频小信号模型
- 双极型晶体管放大电路频率特性
- 单管共射高频特性
- 重要分析方法:
频率特性概述
频率特性基本概念
- 幅频特性和相频特性: 频率特性包括幅频特性和相频特性, 前者指放大电路增益的大小随频率变化的关系, 后者则说明不同频率的信号在放大过程中所产生的相移随频率变化的关系.
- 将放大电路视为一个有源线性网络, 电路增益用系统传输函数H(s)表示. 通常在复数频域分析传输函数, 设输入, 输出的复频域信号分别为X(s),Y(s). X(s), Y(s)分别是输入, 输出信号的拉普拉斯变换. 则系统传输函数为 H ( s ) = Y ( s ) / X ( s ) H(s)=Y(s)/X(s) H(s)=Y(s)/X(s)
式中, s为复数频率, s = σ + j ω s=\sigma +j\omega s=σ+jω. 当 s = j ω s=j\omega s=jω(或 s = j 2 π f s=j2\pi f s=j2πf)时, H ˙ ( j ω ) \dot H(j\omega) H˙(jω)[或 H ˙ ( j f ) \dot H(jf) H˙(jf)]就是系统的稳态正弦频率响应函数, 简称为频率响应或频率特性. - 对于放大电路, H ˙ v \dot H_v H˙v是电压放大倍数, 可写为 A ˙ v \dot A_v A˙v,即 A ˙ v = V ˙ o V ˙ i = ∣ A ˙ v ( ω ) ∣ e j φ ( ω ) \dot A_v=\frac{\dot V_o}{\dot V_i}=|\dot A_v(\omega)|e^{j\varphi(\omega)} A˙v=V˙iV˙o=∣A˙v(ω)∣ejφ(ω)
∣ A ˙ v ( ω ) ∣ |\dot A_v(\omega)| ∣A˙v(ω)∣表示放大电路电压增益的模值与频率 ω ( ω = 2 π f ) \omega(ω=2\pi f) ω(ω=2πf), 称其为放大电路的幅频特性. φ ( ω ) \varphi (\omega) φ(ω)表示放大电路输 出电压与输入电压之间的相位差 φ \varphi φ与角频率 ω \omega ω之间的关系, 称其为相频特性. - 工作频段, 截止频率, 通频带
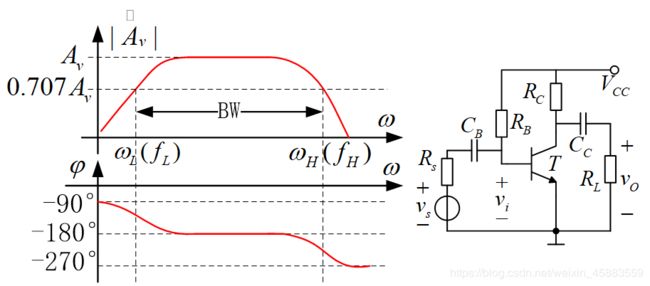
上图放大电路中, 输入信号为 V ˙ s \dot V_s V˙s, 输出信号为 V ˙ o \dot V_o V˙o, 左侧上下分别为这一电路的电压传输函数 A ˙ v = V ˙ o / V ˙ s = ∣ A ˙ v ( f ) ∣ e j φ ( f ) \dot A_v=\dot V_o/\dot V_s=|\dot A_v(f)|e^{j\varphi (f)} A˙v=V˙o/V˙s=∣A˙v(f)∣ejφ(f)的幅频特性 ∣ A ˙ v ( f ) ∣ |\dot A_v(f)| ∣A˙v(f)∣和相频特性 φ ( f ) \varphi(f) φ(f)的函数曲线图. - 有幅频特性曲线可见, 放大电路对各频率成分的放大倍数并不相同. 低频段时, 幅频和相频曲线平坦, 基本上为常数, 保持一定的电压增益和 − 18 0 o -180^o −180o的相移. 在低频段, 耦合电容和旁路电容不可以看作短路, 电压增益随信号频率的减小而减小, 相移减小. 在高频段, 晶体管的极间电容不能视为交流信号开路, 此时电压增益随信号频率增加而减小, 相移增大. 一般低频段的输出电压有超前于中频时的附加相移, 高频段的输出电压有滞后于中频的附加相移.
- 在低频段, 使电压增益下降为中频段增益 A v m A_{vm} Avm的 1 / 2 1/\sqrt2 1/2(相当于0.707倍)时的频率称为下限截止频率 f L f_L fL, 简称下截频; 高频段时, 使电压增益下降为中频段增益 A v m A_{vm} Avm的 1 / 2 1/\sqrt2 1/2时的频率称为上限截止频率 f H f_H fH(上截频). 从 f L f_L fL到 f H f_H fH的频段称为放大电路的通频带, 用BW表示, 即 B W = f H − f L BW=f_H-f_L BW=fH−fL
通常所说的放大电路增益一般都是中频增益. 由于截止频率处的功率传输函数恰为其中频值得一半, 因此截止频率也称半功率点. - 幅度失真和相位失真
幅度失真: 如果放大电路的通频带不够宽, 使电路对不同频率分量的增益不同, 从而引起输出信号中各频率分量的幅度比例发生了变化, 导致输出波形的失真.
相位失真: 如果放大电路的相移和频率关系不是线性的, 不同频率分量的信号通过放大电路后产生的时延不同而引起的失真.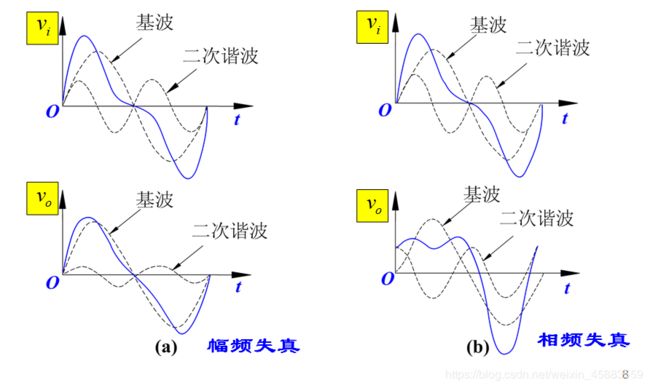
由于幅度失真和相位失真都是由线性电抗元件引起的, 因此又称为线性失真. 其特点是输出波形中没有产生新的频率. 若在输出波形中产生了输入信号没有的新频率, 则成为非线性失真. - 传输函数, 零点, 极点
在复数频率s域中, 电容的容抗为 1 / s C 1/sC 1/sC, 电感的感抗为 s L sL sL, 因而含有电抗成分的线性系统的传输函数 A s A_s As的一般表达式为 A ( s ) = Y ( s ) X ( s ) = b m s m + b m − 1 s m − 1 + . . . + b 1 s + b 0 a n s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 A(s)=\frac{Y(s)}{X(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+...+b_1s+b_0}{a_ns^n+a_{n-1}s^{n-1}+...+a_1s+a_0} A(s)=X(s)Y(s)=ansn+an−1sn−1+...+a1s+a0bmsm+bm−1sm−1+...+b1s+b0
将分母, 分子分别求根, 可将其写为 A ( s ) = K ( s − z 1 ) ( s − z 2 ) . . . ( s − z m ) ( s − p 1 ) ( s − p 2 ) . . . ( s − p n ) A(s)=K\frac{(s-z_1)(s-z_2)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)} A(s)=K(s−p1)(s−p2)...(s−pn)(s−z1)(s−z2)...(s−zm)
乘 z i z_i zi为传输函数的零点, p i p_i pi为传输函数的极点. 一个稳定的电子电路系统的零, 极点应满足两个基本条件:
(1). 零点个数小于等于极点个数
(2). 极点应是负实数或是实部为负的共轭复数对
(3). 有非独立电容的电路, 极点个数小于电容数

令 s = j ω s=j\omega s=jω, 得到系统的频率响应函数 A ˙ ( ω ) \dot A(\omega) A˙(ω), 在各 p i , z i p_i, z_i pi,zi均为实数的情况下, 令 − p i = ω p i , − z i = ω z i . ω p i , ω z i -p_i=\omega_{pi}, -z_i=\omega_{zi}. \ \omega_{pi},\omega_{zi} −pi=ωpi,−zi=ωzi. ωpi,ωzi分别被称为极点角频率, 零点角频率.则 A ˙ ( ω ) \dot A(\omega) A˙(ω)的表达式为 A ˙ ( ω ) = K ( j ω + ω z 1 ) ( j ω + ω z 2 ) . . . ( j ω + ω z m ) ( j ω + ω p 1 ) ( j ω + ω p 2 ) . . . ( j ω + ω p n ) \dot A(\omega)=K\frac{(j\omega +\omega_{z1})(j\omega+\omega_{z2})...(j\omega+\omega_{zm})}{(j\omega +\omega_{p1})(j\omega+\omega_{p2})...(j\omega+\omega_{pn})} A˙(ω)=K(jω+ωp1)(jω+ωp2)...(jω+ωpn)(jω+ωz1)(jω+ωz2)...(jω+ωzm)
根据 A ˙ ( ω ) \dot A(\omega) A˙(ω)可以得到幅频响应函数和相频响应函数.

对于多级放大电路, 总电压增益为各级增益之积, 总相移等与各级相移之和. 
频率特性分析基本方法
- 波特图: 幅频特性的波特图使用分贝作为纵坐标, 每十倍频率间隔作为横坐标.
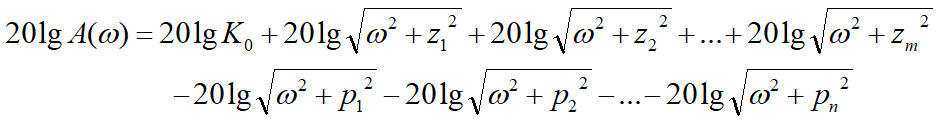
或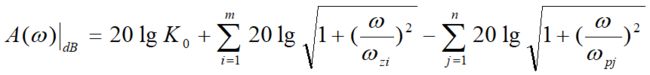
即: 总传输幅频特性(增益)为各零极点的代数和(差).- 一阶实数极点波特图.
低通电路稳定响应为: A ˙ v ( j ω ) = 1 1 + j ω R C = 1 1 + j ω / ω p , ω p = 1 R C \dot A_v(j\omega)=\frac{1}{1+j\omega RC}=\frac{1}{1+j\omega/\omega_p}, \omega_p=\frac{1}{RC} A˙v(jω)=1+jωRC1=1+jω/ωp1,ωp=RC1- 幅频特性: ω p \omega_p ωp为极点角频率, 幅频特性可表示为 A ( ω ) = 1 1 + ( ω / ω p ) 2 或 A ˙ v ( j f ) = 1 1 + j f / f p , ω = 2 π f 20 lg A ( ω ) = − 20 lg 1 + ( ω / ω p ) 2 A(\omega)=\frac{1}{\sqrt{1+(\omega/\omega_p)^2}}\\[2ex] 或\dot A_v(jf)=\frac{1}{1+jf/f_p}, \omega=2\pi f\\[2ex] 20\lg A(\omega)=-20\lg\sqrt{1+(\omega/\omega_p)^2} A(ω)=1+(ω/ωp)21或A˙v(jf)=1+jf/fp1,ω=2πf20lgA(ω)=−20lg1+(ω/ωp)2
当 ω < < ω p \omega<<ω_p ω<<ωp时, 20lgA(ω)为0
当ω= ω p \omega_p ωp时, 20lgA(ω)约为-3dB
当ω>> ω p \omega_p ωp时, 20lgA(ω)为以-20dB/十倍频率下降的直线
幅频特性可近似由上述三部分组成, 误差最大点在 ω p ω_p ωp, 误差为3dB., ω p \omega_p ωp称为上限截止频率.

- 相频特性:
A ( ω ) = 1 1 + ( ω / ω p ) 2 φ ( ω ) = − arctan ( ω / ω p ) A(\omega)=\frac{1}{\sqrt{1+(\omega/\omega_p)^2}}\\[2ex] \varphi(\omega)=-\arctan (\omega/\omega_p) A(ω)=1+(ω/ωp)21φ(ω)=−arctan(ω/ωp)
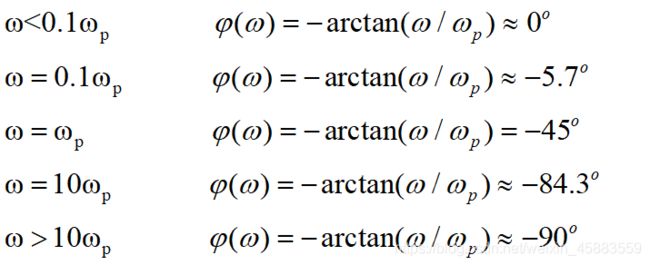
可用三条直线(频率用十倍频程)描述相频特性, 最大误差在0.1 ω p \omega_p ωp和 ω p \omega_p ωp处, 误差为5.7度. ω p \omega_p ωp为上限截止频率
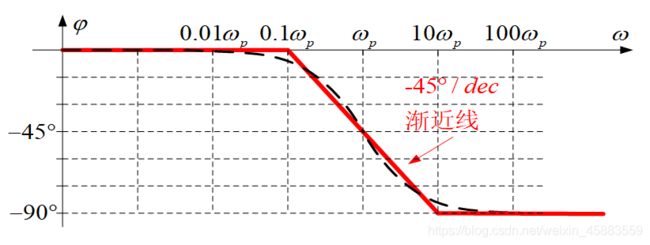
- 幅频特性: ω p \omega_p ωp为极点角频率, 幅频特性可表示为 A ( ω ) = 1 1 + ( ω / ω p ) 2 或 A ˙ v ( j f ) = 1 1 + j f / f p , ω = 2 π f 20 lg A ( ω ) = − 20 lg 1 + ( ω / ω p ) 2 A(\omega)=\frac{1}{\sqrt{1+(\omega/\omega_p)^2}}\\[2ex] 或\dot A_v(jf)=\frac{1}{1+jf/f_p}, \omega=2\pi f\\[2ex] 20\lg A(\omega)=-20\lg\sqrt{1+(\omega/\omega_p)^2} A(ω)=1+(ω/ωp)21或A˙v(jf)=1+jf/fp1,ω=2πf20lgA(ω)=−20lg1+(ω/ωp)2
- 一阶零点因子波特图: A ( j ω ) = 1 + j ω / ω z A(j\omega)=1+j\omega/\omega_z A(jω)=1+jω/ωz(不存在)
- 幅频特性: A ( ω ) = 1 + ( ω / ω z ) 2 A(\omega)=\sqrt{1+(\omega/\omega_z)^2} A(ω)=1+(ω/ωz)2
当 ω < < ω z \omega<<\omega_z ω<<ωz时, 20 lg A ( ω ) ≈ 0 20\lg A(\omega)\approx0 20lgA(ω)≈0
当 ω = ω z \omega=\omega_z ω=ωz, 20 lg A ( ω ) = 3 d B 20\lg A(\omega)=3dB 20lgA(ω)=3dB
当 ω > > ω z \omega>>\omega_z ω>>ωz, 以20dB/十倍频上升.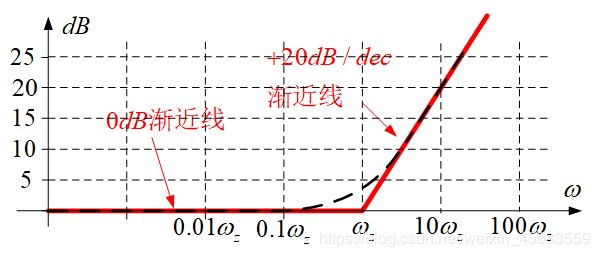
- 相频特性:
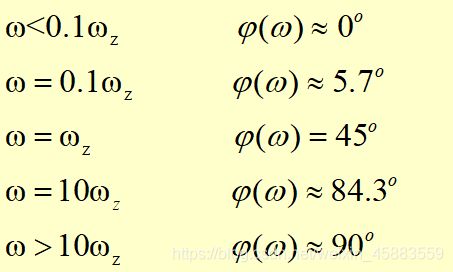
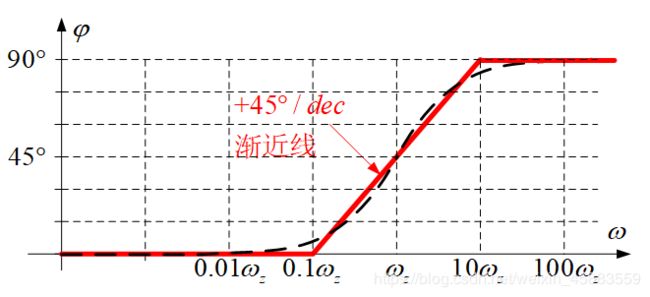
- 幅频特性: A ( ω ) = 1 + ( ω / ω z ) 2 A(\omega)=\sqrt{1+(\omega/\omega_z)^2} A(ω)=1+(ω/ωz)2
- RC高通电路波特图:
A v ( j ω ) = 1 1 + ω L / j ω = j ω / ω L 1 + j ω / ω L A_v(j\omega)=\frac{1}{1+\omega_L/j\omega}=\frac{j\omega/\omega_L}{1+j\omega/\omega_L} Av(jω)=1+ωL/jω1=1+jω/ωLjω/ωL
ω L \omega_L ωL处是0dB, 处于 ω \omega ω=0处的零点, ω = ω L \omega=\omega_L ω=ωL是一个极点.
幅频特性表达为:
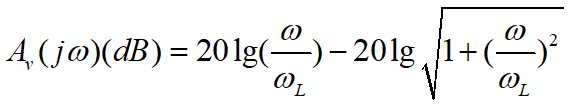
eg:
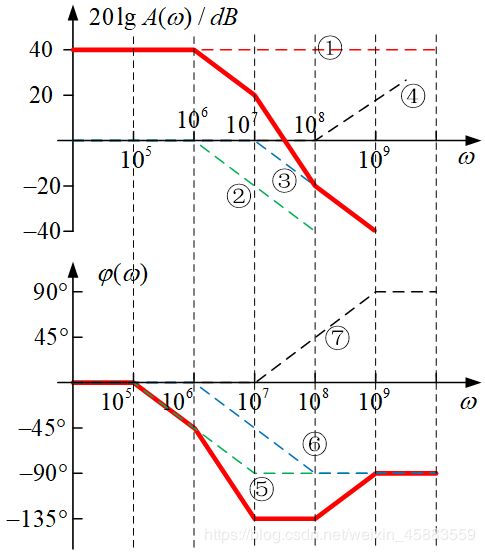
- 一阶实数极点波特图.
多级放大电路增益的频率特性.
- 幅频特性, 相频特性
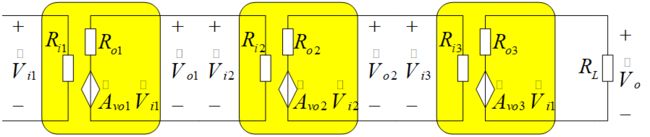

多级放大电路幅频特性为各单机放大电路幅频特性之积(分贝数之和), 相频特性为各单级放大电路相频特性之和. - 截止频率和通频带: 对于n级放大电路, 若各级上下限频率分别为 f L 1 . . f L n , f H 1 , , , f H n f_{L1}..f_{Ln},f_{H1},,,f_{Hn} fL1..fLn,fH1,,,fHn,整个电路上下截频分别为 f L , f H f_L,f_H fL,fH, 由于 20 lg ∣ A ˙ v ∣ = ∑ k = 1 n 20 lg ∣ A ˙ v k ∣ 20\lg|\dot A_v|=\sum_{k=1}^n20\lg|\dot A_{vk}| 20lg∣A˙v∣=∑k=1n20lg∣A˙vk∣, 求解使增益下降3dB的频率, 忽略高次项, 并修正: f L = 1.1 ∑ k = 1 n f L k 2 , 1 f H = 1.1 ∑ k = 1 n 1 f H k 2 f_L=1.1\sqrt{\sum_{k=1}^n f^2_{Lk}},\ \ \ \frac{1}{f_H}=1.1\sqrt{\sum_{k=1}^n\frac{1}{f^2_{Hk}}} fL=1.1k=1∑nfLk2, fH1=1.1k=1∑nfHk21
- 主极点: 在低通系统中若频率最低的极点比其他零极点小得多(小于离他最近的极点1/4以下), 则称该极点为主极点. 其他零极点对该频率处的幅度影响可以忽略.(相位影响不可以忽略, 若忽略应0.1以下). 同样, 若高通系统中频率最高的极点比其他零极点高得多, (大于4倍以上), 则称该极点为主极点.
eg:
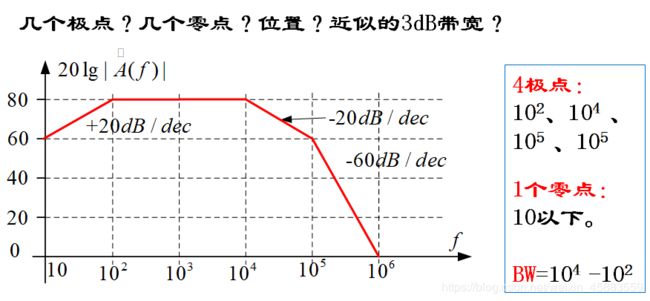
分析: 零点使直线向上20bB/10倍频率, 因此有一个零点在10之前, 极点使直线向下, 故 1 0 2 10^2 102一个极点, 1 0 4 10^4 104一个极点, 1 0 5 10^5 105两个极点. 通频带为 1 0 4 − 1 0 2 10^4-10^2 104−102, 带宽通过上面的公式, 上截频由一个零点确定, 下截频由4个极点确定.
晶体管结电容对高频特性的影响
高频小信号模型
- 密勒定理:
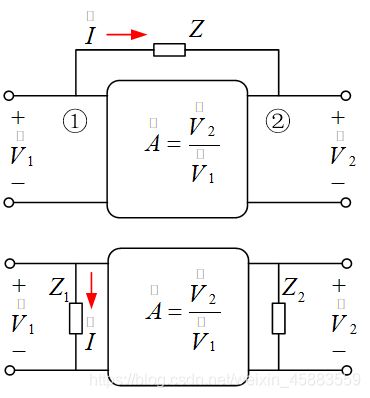
对于节点1:
对于结点2: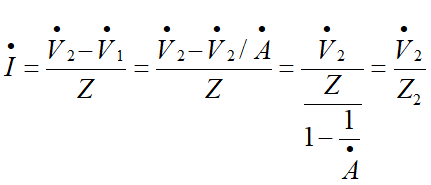
即:
- 密勒定理化简高频模型: C b ′ c C_{b'c} Cb′c跨在输入和输出回路之间, 不便计算, 利用密勒定理将 C b ′ c C_{b'c} Cb′c的影响变换到输入回路和输出回路, 计算得$ C M = ( 1 − A ˙ ) C b ′ c , C M ′ = A ˙ − 1 A ˙ C b ′ c C_M=(1-\dot A)C_{b'c}, C_M'=\frac{\dot A-1}{\dot A}C_{b'c} CM=(1−A˙)Cb′c,CM′=A˙A˙−1Cb′c
由于结电容的影响, 频率升高, 晶体管放大倍数下降, β \beta β使频率的函数, 用 β ˙ \dot \beta β˙表示. 低频时, β用 β 0 \beta_0 β0表示. 当频率增大时, 使得 ∣ β ˙ ∣ |\dot\beta| ∣β˙∣下降到 β 0 / 2 \beta_0/\sqrt2 β0/2的频率为 β ˙ \dot \beta β˙的共射截止频率 f β f_\beta fβ, ∣ β ˙ ∣ = 1 |\dot\beta|=1 ∣β˙∣=1时对应的频率称特征频率 f T f_T fT, f T > f β f_T>f_\beta fT>fβ

- 晶体管参数:

根据上图, 令c,e短路, 得到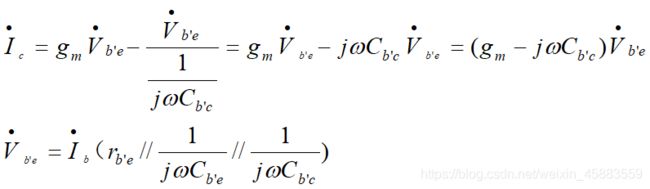
解得: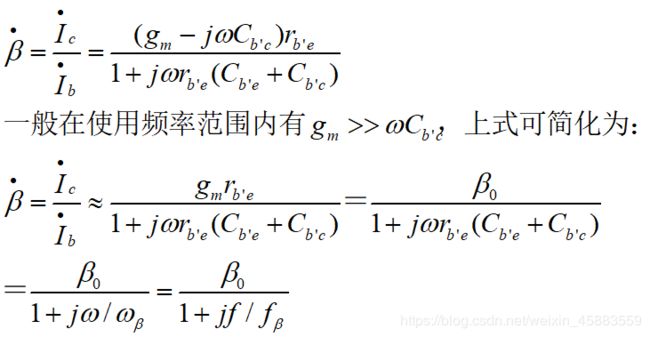

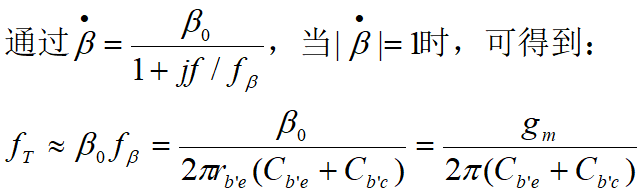

得到三个频率特性参数的关系: f α > f T > f β f_\alpha>f_T>f_{\beta} fα>fT>fβ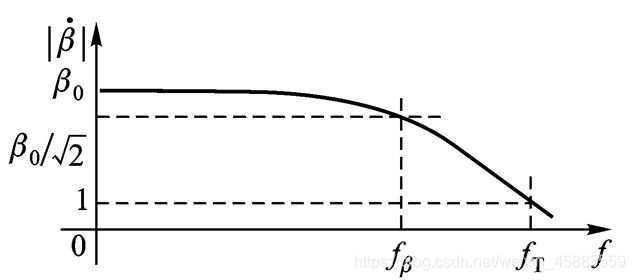
双极型晶体管放大电路频率特性
- 高频段: 受晶体管高频参数(结电容)的影响, 放大电路的放大能力会随工作频率的增到而减弱(海域晶体管的工作组态, 负载电阻, 信号源内阻有关).
- 低频段: 受电路中存在耦合电容或旁路电容的影响, 电路的放大能力也会随工作频率的降低而减弱.
单管共射高频特性
- 共射放大电路单向化等效电路:
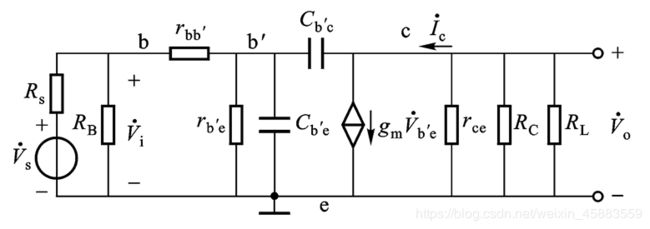
由上图可知, 输出电压
近似为放大器的中频增益, 再利用密勒效应, 得到高频微变等效电路:
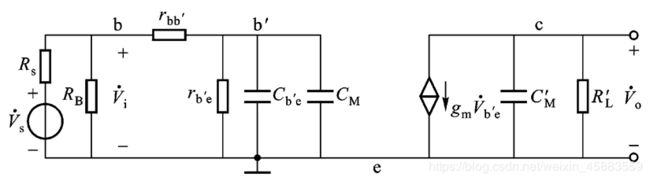
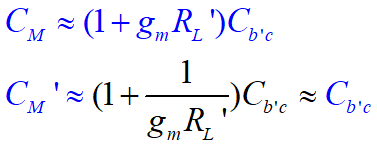
由于共射放大电路放大能力比较强, ∣ A ˙ ∣ > > 1 |\dot A|>>1 ∣A˙∣>>1, 显然有 C M > > C b ′ c C_M>>C_{b'c} CM>>Cb′c, 而 C M ′ ≈ C b ′ c C_M'\approx C_{b'c} CM′≈Cb′c比较小, 一般情况下 C M ′ C_M' CM′的容抗远远大于集电极总负载电阻 R L ′ R_L' RL′, C M ′ C_M' CM′中的电流可以忽略不记, 所以上图可以简化成下图, 期中 C 1 = C b ′ e + C M C_1=C_{b'e}+C_M C1=Cb′e+CM, 并利用戴维南等效定理继续化简
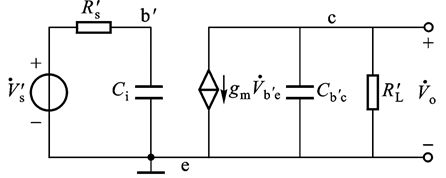
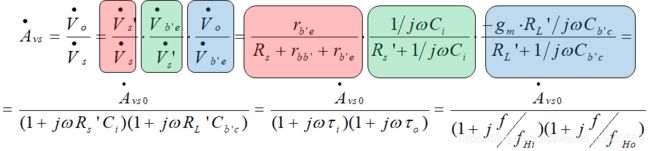
输入回路的时间常数 τ i = R s ′ ⋅ C i \tau_i=R_s'\cdot C_i τi=Rs′⋅Ci, f H i = 1 2 π τ i f_{Hi}=\frac{1}{2\pi\tau_i} fHi=2πτi1其中, f H o > > f H i f_{Ho}>>f_{Hi} fHo>>fHi, 可忽略该极点.

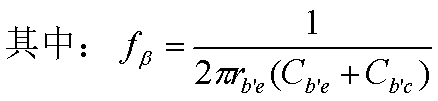
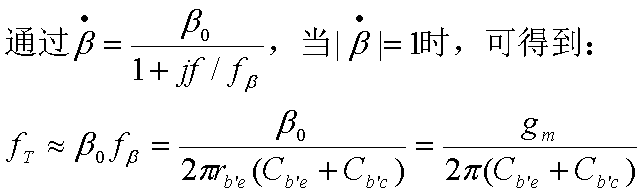

重要分析方法:
- 利用密勒效应求等效电容

- 求输入电路的源电压增益
- 求输入,输出回路的时间常数(等效电阻之积)
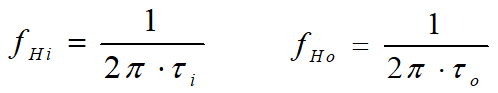
共射电路一般输入回路的极点为主极点. - 估算 A ˙ v = V ˙ o / V ˙ i \dot A_v=\dot V_o/\dot V_i A˙v=V˙o/V˙i, 上截频 f H 1 f_{H1} fH1
- 综合分析: A ˙ v \dot A_v A˙v和 f H f_H fH反映了信号源内阻 R S R_S RS趋于0时共射放大电路的高频特性和上限截止频率.
单管共射放大电路的高频放大特性通常主要取决于其输入回路, 为提高电压增益的上截至频率, 应减小输入回路的时间常数. 为此可采取以下措施:- 选择 r b b ′ 小 , C b ′ c 小 , f T r_{bb'}小,C_{b'c}小, f_T rbb′小,Cb′c小,fT高的晶体管.
- 减小信号源内阻
- 减小负载电阻及管的直流工作点电流, 使 C b ′ c C_{b'c} Cb′c的密勒电容随之减小, 但这也会导致中频增益减小.
- 增益带宽积: 放大电路中的中频电压增益与上截止频率的乘积称为增益带宽积, 对于单管共射电路, 当 f H ≈ f h i f_H\approx f_{hi} fH≈fhi时,
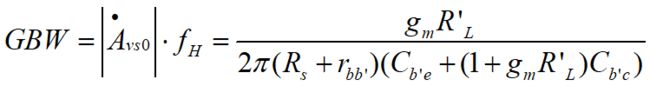
增益带宽积一般为一常数.