scipy.stats.norm
参考:https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html
首先来看下stats模块。Scipy的stats模块包含了多种概率分布的随机变量,随机变量分为连续和离散两种。所有连续随机变量都是rv_continuous的派生类的对象,而所有的离散随机变量都是rv_discrete的派生类的对象。
可以使用下面的语句获得stats模块中的所有的连续随机变量:
from scipy import stats
print([k for k,v in stats.__dict__.items() if isinstance(v,stats.rv_continuous)])
输出:
['genpareto', 'kappa4', 'pareto', 'genexpon', 'dweibull', 'frechet_l', 'fisk', 'erlang', 'exponpow',
'gumbel_r', 'nakagami', 't', 'mielke', 'rdist', 'gausshyper', 'triang', 'levy_stable', 'halfnorm',
'skewnorm', 'cosine', 'kstwobign', 'gumbel_l', 'invgamma', 'johnsonsu', 'expon', 'norm',
'truncnorm', 'dgamma', 'kappa3', 'gennorm', 'foldnorm', 'halfgennorm', 'pearson3', 'exponweib',
'truncexpon', 'loggamma', 'tukeylambda', 'rice', 'uniform', 'powernorm', 'genlogistic',
'recipinvgauss', 'reciprocal', 'gengamma', 'lomax', 'alpha', 'laplace', 'hypsecant', 'ksone', 'ncf',
'vonmises', 'maxwell', 'fatiguelife', 'loglaplace', 'levy', 'genextreme', 'chi2', 'argus', 'burr12',
'johnsonsb', 'frechet_r', 'gilbrat', 'invweibull', 'ncx2', 'semicircular', 'wrapcauchy', 'gamma',
'levy_l', 'weibull_max', 'bradford', 'invgauss', 'gompertz', 'cauchy', 'chi', 'powerlognorm',
'weibull_min', 'wald', 'halfcauchy', 'powerlaw', 'exponnorm', 'beta', 'arcsine', 'f',
'halflogistic', 'vonmises_line', 'trapz', 'anglit', 'burr', 'lognorm', 'betaprime', 'logistic',
'nct', 'rayleigh', 'foldcauchy', 'genhalflogistic']
连续随机变量对象都有如下方法:
- rvs:对随机变量进行随机取值,可以通过size参数指定输出的数组的大小。
- pdf:随机变量的概率密度函数
- cdf:随机变量的累积分布函数,它是概率密度函数的积分
- sf:随机变量的生存函数,它的值是1-cdf(t)
- ppf:累积分布函数的反函数
- stats:计算随机变量的期望值和方差
- fit:对一组随机采样进行拟合,找出最合适取样数据的概率密度函数的系数。
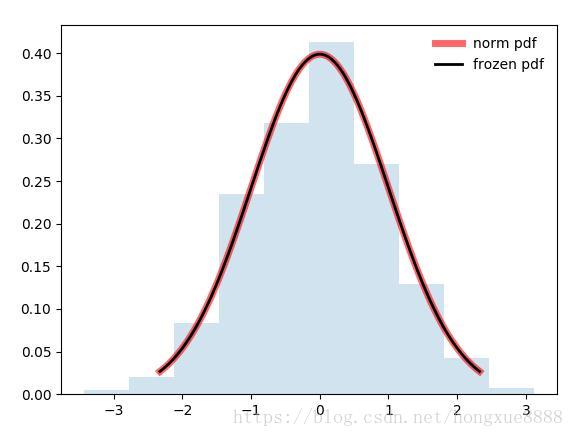
接下来看下scipy.stats.norm例子:
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
mean, var, skew, kurt = norm.stats(moments='mvsk')
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
ax.plot(x, norm.pdf(x), 'r-', lw=5, alpha=0.6, label='norm pdf')
rv = norm()
ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
vals = norm.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], norm.cdf(vals))
r = norm.rvs(size=1000)
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
输出: