二维数组的查找（编程题目）

题目描述：在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

题目分析

  任何一道算法题，在拿到题目之后，都是首先从基础的题干入手，了不起我看不懂任何题干中的隐藏信息，我直接暴力求解，起码让自己有一定的思路，先能解决问题，对于笔试题目的编程，有可能由于测试用例的量级比较小，直接求解了。而且对于一般的问题（排除很明显的动态规划、或者贪心算法暗示，这种题目暴力法很可能达到指数复杂度）。最最最传统的暴力法没有意义，不做讲解，首先抓住题干中的行（列）内有序，大不了这个有序就可以使用二分查找，同时也要认清楚线性有序，有序基本上必然和二分查找分不开了。

暴力求解$O(nlgn)$

  首先来讲解暴力求解，如上分析，这个暴力求解不是指$O(n^2)$复杂度的暴力求解，大不了对行内使用二分查找，这样就可以把行内的查找复杂度降低到$O(nlgn)$，但是这样最致命的缺点就是还有一个题干的信息没有用到，这就是列内也是有序的。

python代码如下：

class SolutionForce():
    def Find(self, target, arrays):
        for array in arrays:
            if self.binaryFind1d(array, target, 0, len(array) - 1):
                return True
        return False

    def binaryFind1d(self,array1d,target,beg,end):
        # 这里只需要判断是否找到，一般二分查找返回的是索引
        mid=(beg+end)>>1 # 右移一位，相当于除二
        if target==array1d[mid]:
            return True
        if target<array1d:
            return self.binaryFind1d(array1d,target,beg,mid-1)
        else:
            return self.binaryFind1d(array1d,target,mid+1,end)

  核心代码是一个一维的二分查找，复杂度刚才分析过了，对一行进行查找是$O(lgn)$，然后需要对n行都执行一个二分查找，最终复杂度是$O(nlgn)$。值得注意的是，在数据量比较小的情况下，代码的执行时间很可能是超过最暴力的方式，复杂度是$O(n^2)$的python代码，因为那个时候可以使用python的list内建关键字 in 来判断，而内建函数的执行速度是很快的。

技巧法$O(n)$

  读到题目，能发现一件很有趣的事情，既然行从前往后有序，列从上往下有序，那么说起来，是否就意味着，每个矩形最左下的元素，正好就是一行最小的，一列最大的元素，从上往下拐个直角弯，这个序列正好是有序的（矩形右上角元素也具备类似的性质）。如果对这个序列执行二分查找，事实上不会降低算法复杂度，因为还是要执行n次二分查找，每次查找的序列长度也是n的线性函数。
  但是我们不去对序列二分查找了，如果直接去查找矩形，和矩形最左下的元素去比较，如果查找值比该元素小，每次可以丢掉比该元素大的一行元素，如果查找值比该元素大，每次可以丢掉比该元素小的一列元素。这样相当于每一次比较多把问题规模减小了一行或者一列，而最多有n行n列，那么问题最差的复杂度就是$O(n)$。

如下数组，以查找13为例。

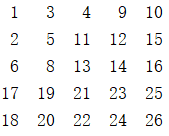
  首先13和18对比，13比18小，丢掉比18大的最后一行，矩形变为4×5，然后此时和17对比，再丢掉一行，此时数据变为3×5，然后和6对比，丢掉6所在的一列，矩形变为3×4，和8对比丢掉一列，数据变为3×3，最后和13对比查找成功。查找失败就相当于把整个矩阵都丢弃，也没有找到。

python代码如下

class SolutionO_n:
    def Find(self,target,array):
        h,v=len(array)-1,0
        while(h>=0 and v<=len(array[0])):
            if array[h][v]==target:
                return True
            if array[h][v] > target:
                h-=1
            else:
                v+=1
        return False

二维二分查找法$O(lgn)$

  既然想到一维二分查找，那么是否也有二维二分查找，如果整个数组都是有序的，相当于还是一维数组的二分查找，不过是对行和列加了一些限制而已，有没有真正意义上的矩阵里查找。还是和中间元素(行的中间，列的中间)对比，显然左上的元素一定比它小，因为有$x_{i-1,j-1}<x_{i,j-1}<x_{i,j}$，右下角元素一定比它大。那如果查找过程中，如果待查找的元素比当前元素小，那么右下角的元素就可以不去对比了，反之，如果大，左上角的元素一定不需要对比了。
  简而言之，就是通过一次与矩形中心对比，这样可以丢掉矩形大约1/4的元素，可以证明，当问题规模按照比例减少的时候，则算法的复杂度则是$O(lgn)$。
  如果以矩形为例， 想要查找举行中14的元素，则直接和矩阵最中心的元素$i=\frac{0+4}{2}=2,j=\frac{0+4}{2}=2$的元素，待查找元素14比当前元素13大，所以丢掉左上方的元素，只需要查找剩下的部分，绿色框区域，而绿色框区域又可以分成两个矩形，然后继续递归执行查找。

  同理，如果待查找元素比当前元素小，则可以丢掉右下角的所有元素，剩下的区域同样可以分成两个矩形，至于矩形如何划分不重要，重要的是递归过程中不要漏掉不能排除的元素，也尽量不要引入重复计算。

  查找整个矩阵，如果没有找到则表明查找失败，需要判断是否查找成功则返回 bool 值，如果需要返回索引，查找失败则返回-1，中间递归返回$max$两部分的返回索引。

python代码如下

class Solution_lgn:
    # array 二维列表
    def Find(self, target, array):
        return self.binary_find(array, target, 0, len(array) - 1, 0, len(array[0]) - 1)

    def binary_find(self, array, target, up, down, left, right):
        if down < up or right < left:
            return False
        h = (up + down) // 2
        v = (left + right) // 2
        if target == array[h][v]:
            return True
        if target < array[h][v]:
            return self.binary_find(array, target, h , down, left, v-1) or self.binary_find(array, target, up, h-1,left, right)
        else:
            return  self.binary_find(array, target, h + 1, down, left, v) or self.binary_find(array, target, up, down, v + 1, right)

  代码的注释我就不写了，想搞清代码的原理可以阅读文章，理解思路看代码就非常容易了。