凸优化基础学习:凸集、凸函数、凸规划理论概念学习
凸优化基础概念学习
- 1、计算几何是研究什么的?
- 2、计算几何理论中(或凸集中)过两点的一条直线的表达式,是如何描述的?与初中数学中那些直线方程有什么差异?有什么好处?
- 3、凸集是什么? 直线是凸集吗?是仿射集吗?
- 4、三维空间中的一个平面,如何表达?
- 5、更高维度的“超平面”,如何表达?
- 6、什么是“凸函数”定义?什么是Hessen矩阵? 如何判别一个函数是凸函数?f(x)=x^3 函数是凸函数吗?
- 7、什么是“凸规划”?如何判别一个规划问题是凸规划问题。举例说明?
1、计算几何是研究什么的?
计算几何是一门兴起于二十世纪七十年代末的计算机科学的一个分支,主要研究解决几何问题的算法。
计算几何的算法有:判断点是否在直线上、判断两线段是否相交、判断线段和直线是否相交、判断点是否在矩形内、判断线段、折线、多边形是否在矩形内、判断矩形是否在矩形内、判断圆是否在矩形内、判断矩形是否在圆内、判断点是否在多边形内、判断线段是否在多边形内、判断点是否在圆内
判断圆是否在圆内、计算点到线段的最近点、计算点到圆的最近点及点坐标、凸包求法等(来源:[维基百科])
2、计算几何理论中(或凸集中)过两点的一条直线的表达式,是如何描述的?与初中数学中那些直线方程有什么差异?有什么好处?
过两点的一条直线的表达式为 ( y − y 2 ) ( y 1 − y 2 ) = ( x − x 2 ) ( x 1 − x 2 ) \frac{(y-y_2)}{(y_1-y_2)}=\frac{(x-x_2)}{(x_1-x_2)} (y1−y2)(y−y2)=(x1−x2)(x−x2),适用不垂直于x,y轴的直线
直线方程表示为: y = k x + b y=kx+b y=kx+b,适用于不垂直x轴的直线
两点 式的表示方程,表示直线上的两点是确定的,表明这个直线的方程时可求的,而斜截式是要知道直线的斜率和在y轴上的截距。
两点式可以在知道两点之后直接写出直线的方程,而斜截式要根据两点式的方程来计算截距和斜率,表示方程的步骤更为麻烦。
3、凸集是什么? 直线是凸集吗?是仿射集吗?
凸集定义:设集合 D ⊂ R n D \subset R^n D⊂Rn,若对于任意两点 x , y ∈ D x,y \in D x,y∈D,及实数 α ( 0 ≤ α ≤ 1 ) \alpha (0 \leq \alpha \leq 1) α(0≤α≤1),都有:
α x + ( 1 − α ) y ∈ D \alpha x+(1-\alpha)y \in D αx+(1−α)y∈D则称集合D为凸集
常见的凸集有单点集{x},空集 ∅ \emptyset ∅,整个欧式空间 R n R^n Rn
仿射集的定义:设集合 D ⊆ R n D \subseteq R^n D⊆Rn,若对于任意两点 x , y ∈ D x,y \in D x,y∈D,及实数 α ∈ R \alpha \in R α∈R,都有:
α x + ( 1 − α ) y ∈ D \alpha x+(1-\alpha)y \in D αx+(1−α)y∈D则称集合D为仿射集
二维情况下,两点x1,x2的
线性组合为全平面
仿射组合为过这两点的直线
凸组合为连接这两点的线段
凸锥组合为以原点为锥顶并通过这两点的锥。
所以直线属于仿射集,也是凸集。因为任意仿射集和子空间都是凸集。直线、射线、线段都是凸集。
还有一些凸集:
超平面: H = x ∈ R n ∣ a 1 x 1 + a 2 x 2 + … + a n x n = b H={x \in R^n|a_1x_1+a_2x_2+\ldots+a_nx_n=b} H=x∈Rn∣a1x1+a2x2+…+anxn=b
半空间: H + = { x ∈ R n ∣ a 1 x 1 + a 2 x 2 + … + a n x n ≥ b } = { x ∈ R n ∣ a T x ≥ b } H^+=\{x \in R^n|a_1x_1+a_2x_2+\ldots+a_nx_n\geq b\}=\{x\in R^n|a^Tx\geq b\} H+={x∈Rn∣a1x1+a2x2+…+anxn≥b}={x∈Rn∣aTx≥b}
4、三维空间中的一个平面,如何表达?
三维空间中的平面由两个量确定:
1、一个法向量(垂直于该平面的向量) n ⃗ \vec n n
2、一个已知点(位于该平面上的一个点)
平面的方程为 a x + b y + c z − ( a x 0 + b y 0 + c z 0 ) = 0 ax+by+cz-(ax_0+by_0+cz_0)=0 ax+by+cz−(ax0+by0+cz0)=0
平面法向量为: n ⃗ = ( a , b , c ) T \vec n=(a,b,c)^T n=(a,b,c)T
平面一个已知点: P = ( x 0 , y 0 , z 0 ) T P=(x_0,y_0,z_0)^T P=(x0,y0,z0)T
参考博客:三维空间中的平面.
5、更高维度的“超平面”,如何表达?
超平面: H = x ∈ R n ∣ a 1 x 1 + a 2 x 2 + … + a n x n = b H={x \in R^n|a_1x_1+a_2x_2+\ldots+a_nx_n=b} H=x∈Rn∣a1x1+a2x2+…+anxn=b
超平面H是从n维空间到n-1维空间的一个映射子空间,它有一个n维向量和一个实数定义。因为是子空间,所以超平面一定过原点。一条直线是 R2 空间内的超平面,一个平面是 R3 空间内的超平面 。Rn 空间的超平面是Rn 空间内的一个 n - 1 维的仿射子空间。
6、什么是“凸函数”定义?什么是Hessen矩阵? 如何判别一个函数是凸函数?f(x)=x^3 函数是凸函数吗?
凸函数定义:设集合 D ⊂ R n D \subset R^n D⊂Rn是非空凸集, f ( x ) : s → R f(x):s\rightarrow R f(x):s→R,若对任意的 x , y ∈ D x,y\in D x,y∈D,及任意的 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1]都有 f ( α x + ( 1 − α ) y ) ≤ α f ( x ) + ( 1 − α ) f ( y ) f(\alpha x+(1-\alpha)y)\leq \alpha f(x)+(1-\alpha)f(y) f(αx+(1−α)y)≤αf(x)+(1−α)f(y)则称函数f(x)为D上的凸函数。
严格凸函数定义:设集合 D ⊂ R n D \subset R^n D⊂Rn是非空凸集, f ( x ) : s → R f(x):s\rightarrow R f(x):s→R,若对任意的 x , y ∈ D ( x ≠ y ) x,y\in D(x \neq y) x,y∈D(x=y),及任意的 α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)都有 f ( α x + ( 1 − α ) y ) < α f ( x ) + ( 1 − α ) f ( y ) f(\alpha x+(1-\alpha)y)< \alpha f(x)+(1-\alpha)f(y) f(αx+(1−α)y)<αf(x)+(1−α)f(y)则称函数f(x)为D上的严格凸函数。
Hessen矩阵的定义:是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。Hessen矩阵常用于牛顿法解决优化问题,利用Hessen矩阵可判定多元函数的极值问题。详情参考:Hessen矩阵 维基百科.
判断一个函数是凸函数的方法:
任意取两点,这两点的连线上的点,一直在这两点的函数曲线的上方,则这个函数为凸函数。
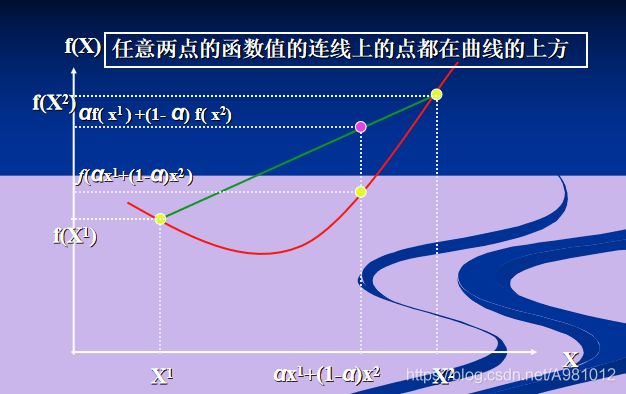
f ( x ) = x 3 f(x)=x^3 f(x)=x3不是凸函数,因为它的图像表示上,任意两点的连线段上的点不是全都在函数曲线的上方,

7、什么是“凸规划”?如何判别一个规划问题是凸规划问题。举例说明?
凸规划定义:若最优化问题的目标函数为凸函数,不等式约束函数也为凸函数,等式约束函数是仿射的,则称该最优化问题为凸规划。
设集合 D ⊆ R n D \subseteq R^n D⊆Rn为凸集,f(x)为D上的凸函数,则称规划问题 m i n x ∈ D f ( x ) min_{x\in D}f(x) minx∈Df(x)为凸规划问题。
min f ( X ) = x 1 2 + x 2 2 − 4 x 1 + 4 f(X)=x_1^2+x_2^2-4x_1+4 f(X)=x12+x22−4x1+4
s t = { g 1 ( X ) = − x 1 + x 2 − 2 ≤ 0 g 2 ( X ) = x 1 2 + x 2 + 1 ≤ 0 x 1 , x 2 ≥ 0 st=\begin{cases} g_1(X)=-x_1+x_2-2\leq 0\\\\ g_2(X)=x_1^2+x_2+1\leq 0\\\\ x_1,x_2\geq 0 \end{cases} st=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧g1(X)=−x1+x2−2≤0g2(X)=x12+x2+1≤0x1,x2≥0
▽ 2 f ( X ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 x 1 ∂ 2 f ∂ x 2 2 ] = [ 2 0 0 2 ] \triangledown ^2 f(X)=\begin{bmatrix}\frac{\partial^2f}{\partial x_1^2} &\frac{\partial^2f}{\partial x_1 \partial x_2} \\\\ \frac{\partial^2f}{\partial x_2x_1} &\frac{\partial^2f}{\partial x_2^2} \end{bmatrix} = \begin{bmatrix}2 & 0\\\\0 &2\end{bmatrix} ▽2f(X)=⎣⎢⎡∂x12∂2f∂x2x1∂2f∂x1∂x2∂2f∂x22∂2f⎦⎥⎤=⎣⎡2002⎦⎤,为正定,凸函数
▽ 2 g 1 ( X ) = [ ∂ 2 g 1 ∂ x 1 2 ∂ 2 g 1 ∂ x 1 ∂ x 2 ∂ 2 g 1 ∂ x 2 x 1 ∂ 2 g 1 ∂ x 2 2 ] = [ 0 0 0 0 ] \triangledown ^2 g_1(X)=\begin{bmatrix}\frac{\partial^2g_1}{\partial x_1^2} &\frac{\partial^2g_1}{\partial x_1 \partial x_2} \\\\ \frac{\partial^2g_1}{\partial x_2x_1} &\frac{\partial^2g_1}{\partial x_2^2} \end{bmatrix} = \begin{bmatrix}0 & 0\\\\0 &0\end{bmatrix} ▽2g1(X)=⎣⎢⎡∂x12∂2g1∂x2x1∂2g1∂x1∂x2∂2g1∂x22∂2g1⎦⎥⎤=⎣⎡0000⎦⎤,为半正定,凸函数
▽ 2 g 2 ( X ) = [ ∂ 2 g 2 ∂ x 1 2 ∂ 2 g 2 ∂ x 1 ∂ x 2 ∂ 2 g 2 ∂ x 2 x 1 ∂ 2 g 2 ∂ x 2 2 ] = [ 2 0 0 0 ] \triangledown ^2 g_2(X)=\begin{bmatrix}\frac{\partial^2g_2}{\partial x_1^2} &\frac{\partial^2g_2}{\partial x_1 \partial x_2} \\\\ \frac{\partial^2g_2}{\partial x_2x_1} &\frac{\partial^2g_2}{\partial x_2^2} \end{bmatrix} = \begin{bmatrix}2 & 0\\\\0 &0\end{bmatrix} ▽2g2(X)=⎣⎢⎡∂x12∂2g2∂x2x1∂2g2∂x1∂x2∂2g2∂x22∂2g2⎦⎥⎤=⎣⎡2000⎦⎤,为半正定,凸函数

可以判断出目标函数为凸函数,Hessen矩阵为正定的,表明有极小值,不等式约束函数也为凸函数,等式约束函数是仿射的
由此可得出该规划为凸规划
例题:验证min f ( X ) = 2 x 1 2 + x 2 2 + 2 x 3 2 + x 1 x 3 − x 1 x 2 + x 1 + 2 x 2 f(X)=2x_1^2+x_2^2+2x_3^2+x_1x_3-x_1x_2+x_1+2x_2 f(X)=2x12+x22+2x32+x1x3−x1x2+x1+2x2
s t = { g 1 ( X ) = − x 1 2 + x 2 2 − x 3 ≤ 0 g 2 ( X ) = x 1 + x 2 + 2 x 3 ≤ 16 g 3 ( X ) = − x 1 − x 2 + x 3 ≤ 0 st=\begin{cases} g_1(X)=-x_1^2+x_2^2-x_3\leq 0\\\\ g_2(X)=x_1+x_2+2x_3\leq 16\\\\ g_3(X)=-x_1-x_2+x_3\leq0 \end{cases} st=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧g1(X)=−x12+x22−x3≤0g2(X)=x1+x2+2x3≤16g3(X)=−x1−x2+x3≤0是凸规划
▽ 2 f ( X ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 1 ∂ x 3 ∂ 2 f ∂ x 2 x 1 ∂ 2 f ∂ x 2 2 ∂ 2 f ∂ x 2 ∂ x 3 ∂ 2 f ∂ x 3 x 1 ∂ 2 f ∂ x 3 ∂ x 2 ∂ 2 f ∂ x 3 2 ] = [ 4 − 1 1 − 1 2 0 1 0 4 ] \triangledown ^2 f(X)=\begin{bmatrix}\frac{\partial^2f}{\partial x_1^2} &\frac{\partial^2f}{\partial x_1 \partial x_2}&\frac{\partial^2f}{\partial x_1 \partial x_3}\\\\ \frac{\partial^2f}{\partial x_2x_1} &\frac{\partial^2f}{\partial x_2^2}&\frac{\partial^2f}{\partial x_2 \partial x_3} \\\\ \frac{\partial^2f}{\partial x_3x_1} &\frac{\partial^2f}{\partial x_3\partial x_2}&\frac{\partial^2f}{\partial x_3 ^2} \end{bmatrix} = \begin{bmatrix}4 & -1 & 1\\\\-1 & 2 &0\\\\1 & 0 & 4\end{bmatrix} ▽2f(X)=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2x1∂2f∂x3x1∂2f∂x1∂x2∂2f∂x22∂2f∂x3∂x2∂2f∂x1∂x3∂2f∂x2∂x3∂2f∂x32∂2f⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡4−11−120104⎦⎥⎥⎥⎥⎤是正定,凸函数
▽ 2 g 1 ( X ) = [ ∂ 2 g 1 ∂ x 1 2 ∂ 2 g 1 ∂ x 1 ∂ x 2 ∂ 2 g 1 ∂ x 1 ∂ x 3 ∂ 2 g 1 ∂ x 2 x 1 ∂ 2 g 1 ∂ x 2 2 ∂ 2 g 1 ∂ x 2 ∂ x 3 ∂ 2 g 1 ∂ x 3 x 1 ∂ 2 g 1 ∂ x 3 ∂ x 2 ∂ 2 g 1 ∂ x 3 2 ] = [ − 2 0 0 0 2 0 0 0 0 ] \triangledown ^2 g_1(X)=\begin{bmatrix}\frac{\partial^2g_1}{\partial x_1^2} &\frac{\partial^2g_1}{\partial x_1 \partial x_2}&\frac{\partial^2g_1}{\partial x_1 \partial x_3}\\\\ \frac{\partial^2g_1}{\partial x_2x_1} &\frac{\partial^2g_1}{\partial x_2^2}&\frac{\partial^2g_1}{\partial x_2 \partial x_3} \\\\ \frac{\partial^2g_1}{\partial x_3x_1} &\frac{\partial^2g_1}{\partial x_3\partial x_2}&\frac{\partial^2g_1}{\partial x_3 ^2} \end{bmatrix} = \begin{bmatrix}-2 &0 & 0\\\\0 & 2 &0\\\\0 & 0 & 0\end{bmatrix} ▽2g1(X)=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2g1∂x2x1∂2g1∂x3x1∂2g1∂x1∂x2∂2g1∂x22∂2g1∂x3∂x2∂2g1∂x1∂x3∂2g1∂x2∂x3∂2g1∂x32∂2g1⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡−200020000⎦⎥⎥⎥⎥⎤是半正定,凸函数
▽ 2 g 2 ( X ) = [ ∂ 2 g 2 ∂ x 1 2 ∂ 2 g 2 ∂ x 1 ∂ x 2 ∂ 2 g 2 ∂ x 1 ∂ x 3 ∂ 2 g 2 ∂ x 2 x 1 ∂ 2 g 2 ∂ x 2 2 ∂ 2 g 2 ∂ x 2 ∂ x 3 ∂ 2 g 2 ∂ x 3 x 1 ∂ 2 g 2 ∂ x 3 ∂ x 2 ∂ 2 g 2 ∂ x 3 2 ] = [ 0 0 0 0 0 0 0 0 0 ] \triangledown ^2 g_2(X)=\begin{bmatrix}\frac{\partial^2g_2}{\partial x_1^2} &\frac{\partial^2g_2}{\partial x_1 \partial x_2}&\frac{\partial^2g_2}{\partial x_1 \partial x_3}\\\\ \frac{\partial^2g_2}{\partial x_2x_1} &\frac{\partial^2g_2}{\partial x_2^2}&\frac{\partial^2g_2}{\partial x_2 \partial x_3} \\\\ \frac{\partial^2g_2}{\partial x_3x_1} &\frac{\partial^2g_2}{\partial x_3\partial x_2}&\frac{\partial^2g_2}{\partial x_3 ^2} \end{bmatrix} = \begin{bmatrix}0 & 0 & 0\\\\0 & 0 &0\\\\0 & 0 & 0\end{bmatrix} ▽2g2(X)=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2g2∂x2x1∂2g2∂x3x1∂2g2∂x1∂x2∂2g2∂x22∂2g2∂x3∂x2∂2g2∂x1∂x3∂2g2∂x2∂x3∂2g2∂x32∂2g2⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡000000000⎦⎥⎥⎥⎥⎤是半正定,凸函数
▽ 2 g 3 ( X ) = [ ∂ 2 g 3 ∂ x 1 2 ∂ 2 g 3 ∂ x 1 ∂ x 2 ∂ 2 g 3 ∂ x 1 ∂ x 3 ∂ 2 g 3 ∂ x 2 x 1 ∂ 2 g 3 ∂ x 2 2 ∂ 2 g 3 ∂ x 2 ∂ x 3 ∂ 2 g 3 ∂ x 3 x 1 ∂ 2 g 3 ∂ x 3 ∂ x 2 ∂ 2 g 3 ∂ x 3 2 ] = [ 0 0 0 0 0 0 0 0 0 ] \triangledown ^2 g_3(X)=\begin{bmatrix}\frac{\partial^2g_3}{\partial x_1^2} &\frac{\partial^2g_3}{\partial x_1 \partial x_2}&\frac{\partial^2g_3}{\partial x_1 \partial x_3}\\\\ \frac{\partial^2g_3}{\partial x_2x_1} &\frac{\partial^2g_3}{\partial x_2^2}&\frac{\partial^2g_3}{\partial x_2 \partial x_3} \\\\ \frac{\partial^2g_3}{\partial x_3x_1} &\frac{\partial^2g_3}{\partial x_3\partial x_2}&\frac{\partial^2g_3}{\partial x_3 ^2} \end{bmatrix} = \begin{bmatrix}0 & 0 & 0\\\\0 & 0 &0\\\\0 & 0 & 0\end{bmatrix} ▽2g3(X)=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2g3∂x2x1∂2g3∂x3x1∂2g3∂x1∂x2∂2g3∂x22∂2g3∂x3∂x2∂2g3∂x1∂x3∂2g3∂x2∂x3∂2g3∂x32∂2g3⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡000000000⎦⎥⎥⎥⎥⎤是半正定,凸函数
由以上可以验证为这个规划为凸规划。
如有错误请指正!