数据结构之二叉排序树BST/二叉查找树/二叉搜索树的创建与删除(动画示例)(非递归)(Java)
目录
- 一、二叉排序树的创建
- 二、二叉排序树的删除
- 三、完整代码
在开始之前,先介绍两个对数据结构学习有帮助的网站。
1. VisuAlgo.net/en
这个网站有好多种数据结构,如链表、哈希图、树、图等,你可以通过各种操作可视化来学习数据结构。里面还有排序算法的动画示例,可以更形象的学习排序算法。


2. BinaryTreeVisualiser
这个网站可以用来学习二叉树,超级好用。

一、二叉排序树的创建
首先要有一个Node类
class Node{
private int num;
private Node left;
private Node right;
public Node(int num) {
this.num=num;
}
public void setNum(int num) {
this.num = num;
}
public int getNum() {
return num;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getLeft() {
return left;
}
public void setRight(Node right) {
this.right = right;
}
public Node getRight() {
return right;
}
}
二叉排序树的创建步骤如下:
- 创建一个根节点root。
- 创建两个指针front、behind。front用于查找比较,behind指向front的父节点(顾名思义,跟在front后面)。front和behind一开始均指向根节点root。
- 创建的过程可以看做多次插入,每次插入新的数都从根节点root开始。
如果要插入的数小于等于front指向的节点的数,front左移;如果要插入的数大于front指向的节点的数,front右移。behind跟在后面。 - 当front==null,则说明找到要插入的位置,直接插入。
/**
* 创建二叉排序树
* @param array 要插入的数
* @return 根节点
*/
public Node create(int[] array) {
setRoot(new Node(array[0])); //创建根节点
Node front,behind;
for(int i=1;i<array.length;i++) {
front=root;
Node temp=new Node(array[i]); //要插入的新节点
while(front!=null) { //front==null就找到了
behind=front; //behind跟在front后面,父节点,每一轮要更新一次
if(temp.getNum()<=front.getNum()) { //小于或等于则左移
front=front.getLeft();
if(front==null)
behind.setLeft(temp);
}else { //大于则右移
front=front.getRight();
if(front==null)
behind.setRight(temp);
}
}
}
return getRoot();
}
二、二叉排序树的删除
二叉排序树的删除步骤如下:(可能有点复杂,多画图,多理解)
- 依旧创建两个指针front、behind,front用于查找,behind指向front的父节点。
- 查找要删除的节点。如果要删除的数小于等于当前节点的数,向左子树查找;如果要删除的数大于当前节点的树,向右子树查找。
- 如果要删除的节点是叶子结点
----如果该节点是根节点,直接将根节点设为null。
----如果该节点不是根节点,则父节点的左/右子指针指向null。(如下图删除18节点)
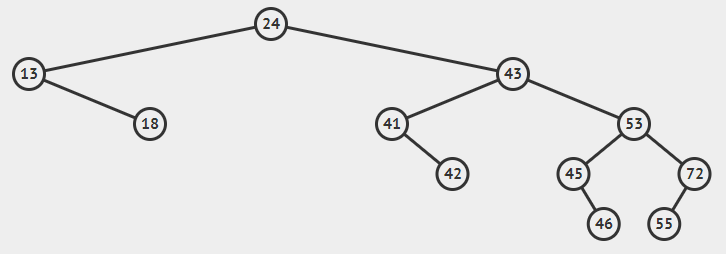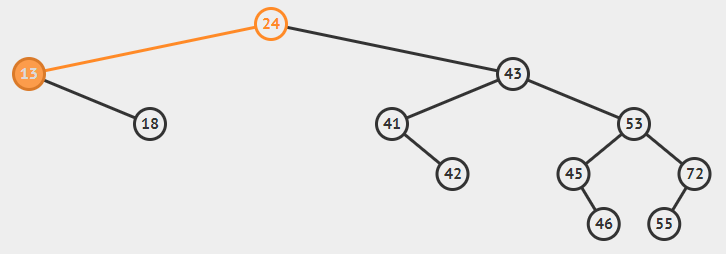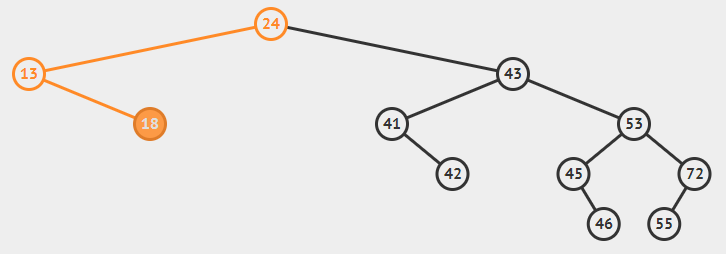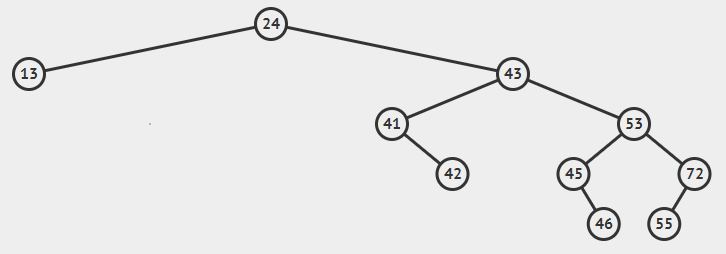
- 如果要删除的节点有一个左/右子节点(可能是子树)
----如果该节点是根节点,则将根节点设置为该节点的左/右子节点。
----如果该节点不是根节点,则父节点的左/右指针指向该节点的左/右子节点。(如下图删除72节点)
- 如果要删除的节点有左、右子节点(可能是子树)
首先,找到左子树最大的节点或右子树最小的节点替换要删的节点(为了保持二叉排序树有序)。我选择了用右子树最小的节点。
从要删除的节点开始,先移向它的右子节点(移动一次),然后一直向其左子树寻找。当找到最左的那个节点,就是右子树的最小节点。
之后先与该最小节点的父节点断绝父子关系,即父节点的左指针设置为null(不然会造成死循环)。同时,如果该最小节点有右子节点(可能是子树),先记录下来,后面可能需要将其插入到合适的位置。(删除45节点,找到最小节点46,46节点就有一坨东西)

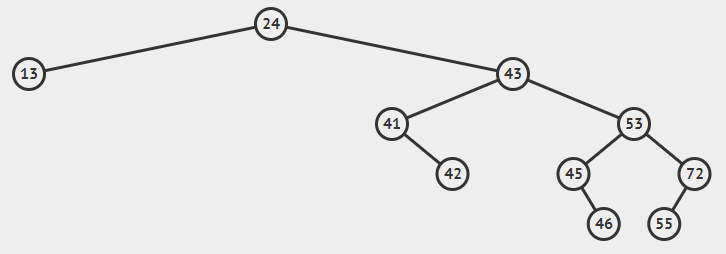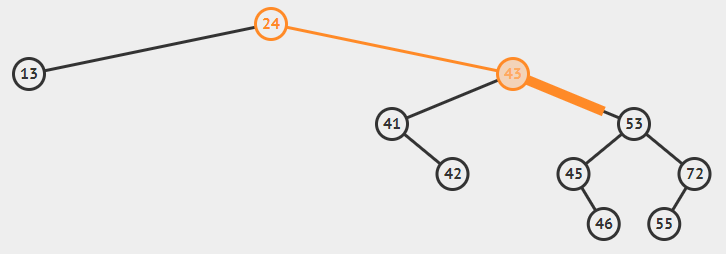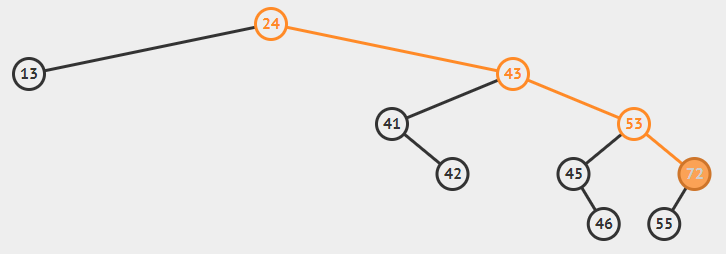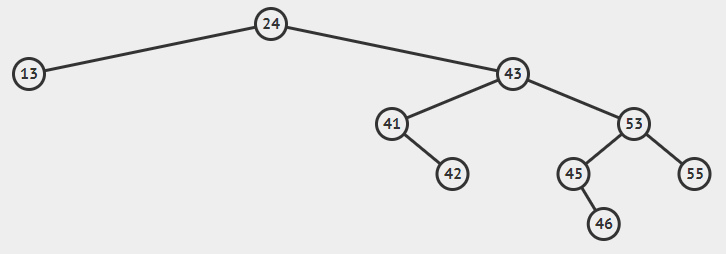
最小节点的左指针指向要删的数的左子节点(最小节点的左指针本来是null),最小节点的右指针指向要删的数的右子节点。但是如果最小节点就是要删节点的右子节点则不改变最小节点的右指针,否则构成死循环,如下面删除53节点,如果最小节点55的右指针指向要删的数的右子节点55,则它就自己指向55自己了。
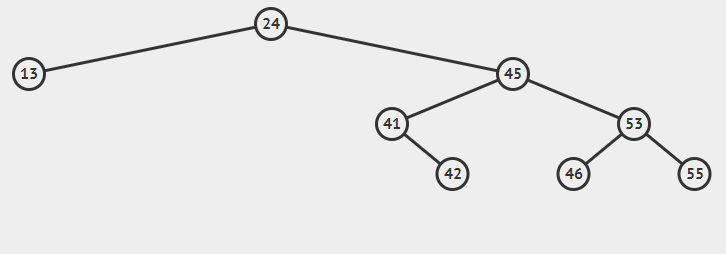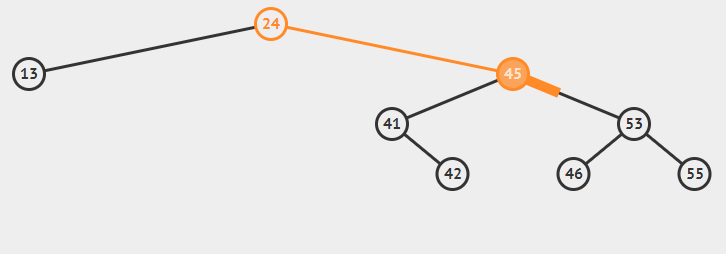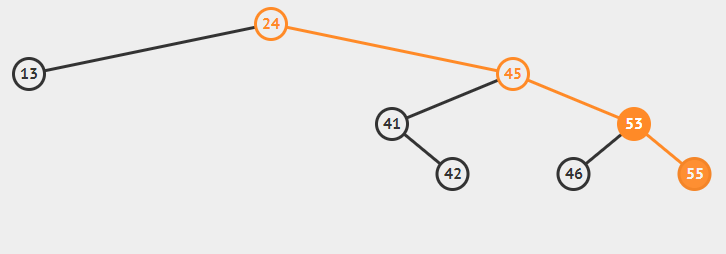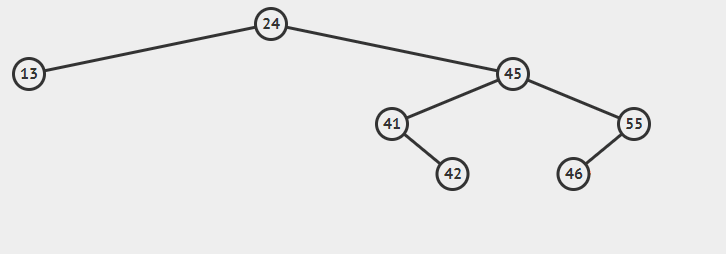
将要删节点的左右指针置为null。
----如果要删除的是根节点,则将根节点设置为最小节点。(如下图删除24节点)

----如果要删除的不是根节点,则要删节点的父节点的右指针指向最小节点。
最后还要将原本最小节点的右子节点(可能是子树)插入到合适的位置。(如果最小节点的右孩子没改变就不用插入)

/**
* 删除二叉排序树节点
* @param num 要删的数
* @return 根节点
*/
public Node delete(int num) {
Node front=root,behind=root;
boolean successful=false;
while(!successful && front!=null) { //删除成功或找不到则结束循环
if(front.getNum()>num) { //要删的数小于当前的数
behind=front; //记录当前节点的位置,删除需要用到父节点
front=front.getLeft(); //左移
}else if(front.getNum()<num) { //要删的数大于当前的数
behind=front; //记录当前节点的位置
front=front.getRight(); //右移
}else { //找到要删的数,front指向这个数,behind是front的父节点
if(front.getLeft()==null && front.getRight()==null) { //要删的是叶子结点
if(front==behind) { //要删的是根节点,根节点没有孩子
setRoot(null); //直接设置null即删除
}else { //叶子结点
if(behind.getLeft()==front) //要删的数是左子节点
behind.setLeft(null);
else //要删的数是右子节点
behind.setRight(null);
}
}else if(front.getLeft()!=null && front.getRight()!=null) { //有两个孩子
//找到左子树最大的节点或右子树最小的节点替换要删的节点
Node min=front.getRight(),temp=min; //指向右子树
while(min.getLeft()!=null) { //找到右子树的最小节点,最小节点的左指针指向null
temp=min; //指向最小节点的父节点
min=min.getLeft();
}
temp.setLeft(null); //断绝父子关系,以免后患
temp=min.getRight(); //如果右孙子,先记录,以后有用
min.setLeft(front.getLeft()); //最小节点的左指针指向要删的数的左子节点
if(front.getRight()!=min) //如果最小节点就是要删节点的右子节点则不改变,否则构成死循环
min.setRight(front.getRight()); //最小节点的右指针指向要删的数的右子节点
front.setLeft(null); //置空左指针
front.setRight(null); //置空有指针
if(front==behind) { //要删的是根节点
setRoot(min); //设置新的根节点
}else {
behind.setRight(min);
}
if(temp!=null&&temp!=min.getRight()) { //最小节点原本有右子树,如果最小节点的右孩子没改变就不用插入
front=min; //front原本指向要删节点,现在节点已经删除,front指向最小节点
while(front!=null) { //将原本最小节点的右子树插入到合适的位置
behind=front;
if(temp.getNum()<=front.getNum()) {
front=front.getLeft();
if(front==null)
behind.setLeft(temp);
}else {
front=front.getRight();
if(front==null)
behind.setRight(temp);
}
}
}
}else if(front.getLeft()!=null) { //要删的数有左子树,没有右子树
if(front==behind) { //要删的是根节点
front=front.getLeft(); //左移一个
behind.setLeft(null);
setRoot(front); //更新根节点
}else {
if(behind.getLeft()==front)
behind.setLeft(front.getLeft());
else
behind.setRight(front.getLeft());
}
}else { //要删的数有右子树,没有左子树
if(front==behind) {
front=front.getRight();
behind.setRight(null);
setRoot(front);
}else {
if(behind.getLeft()==front)
behind.setLeft(front.getRight());
else
behind.setRight(front.getRight());
}
}
successful=true;
}
}
if(successful)
System.out.println("删除成功");
else
System.out.println("删除失败");
return getRoot();
}
三、完整代码
import java.util.Random;
import java.util.Scanner;
import java.util.Stack;
public class BinarySortTree {
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
/**
* 获得随机数组
* @param size
* @return
*/
public static int[] getArray(int size) {
int[] array=new int[size];
Random random=new Random();
for(int i=0;i<array.length;i++)
array[i]=random.nextInt(100);
return array;
}
/**
* 创建二叉排序树
* @param array 要插入的数
* @return 根节点
*/
public Node create(int[] array) {
setRoot(new Node(array[0])); //创建根节点
Node front,behind;
for(int i=1;i<array.length;i++) {
front=root;
Node temp=new Node(array[i]); //要插入的新节点
while(front!=null) { //front==null就找到了
behind=front; //behind跟在front后面,父节点,每一轮要更新一次
if(temp.getNum()<=front.getNum()) { //小于或等于则左移
front=front.getLeft();
if(front==null)
behind.setLeft(temp);
}else { //大于则右移
front=front.getRight();
if(front==null)
behind.setRight(temp);
}
}
}
return getRoot();
}
/**
* 非递归前序遍历
* @param root
*/
public void non_recursive_preOrder(Node root) {
if(root==null)
return;
Node front=root;
Stack<Node> stack=new Stack<Node>();
while(!stack.isEmpty() || front!=null) {
while(front!=null) {
System.out.print(front.getNum()+" ");
stack.push(front);
front=front.getLeft();
}
//此时遍历完左子树
if(!stack.isEmpty()) {
front=stack.pop();
front=front.getRight();
}
}
}
/**
* 插入
* @param num
*/
public void add(int num) {
Node front=root,behind;
Node temp=new Node(num);
while(front!=null) {
behind=front;
if(temp.getNum()<=front.getNum()) {
front=front.getLeft();
if(front==null)
behind.setLeft(temp);
}else {
front=front.getRight();
if(front==null)
behind.setRight(temp);
}
}
}
/**
* 删除二叉排序树节点
* @param num 要删的数
* @return 根节点
*/
public Node delete(int num) {
Node front=root,behind=root;
boolean successful=false;
while(!successful && front!=null) { //删除成功或找不到则结束循环
if(front.getNum()>num) { //要删的数小于当前的数
behind=front; //记录当前节点的位置,删除需要用到父节点
front=front.getLeft(); //左移
}else if(front.getNum()<num) { //要删的数大于当前的数
behind=front; //记录当前节点的位置
front=front.getRight(); //右移
}else { //找到要删的数,front指向这个数,behind是front的父节点
if(front.getLeft()==null && front.getRight()==null) { //要删的是叶子结点
if(front==behind) { //要删的是根节点,根节点没有孩子
setRoot(null); //直接设置null即删除
}else { //叶子结点
if(behind.getLeft()==front) //要删的数是左子节点
behind.setLeft(null);
else //要删的数是右子节点
behind.setRight(null);
}
}else if(front.getLeft()!=null && front.getRight()!=null) { //有两个孩子
//找到左子树最大的节点或右子树最小的节点替换要删的节点
Node min=front.getRight(),temp=min; //指向右子树
while(min.getLeft()!=null) { //找到右子树的最小节点,最小节点的左指针指向null
temp=min; //指向最小节点的父节点
min=min.getLeft();
}
temp.setLeft(null); //断绝父子关系,以免后患
temp=min.getRight(); //如果右孙子,先记录,以后有用
min.setLeft(front.getLeft()); //最小节点的左指针指向要删的数的左子节点
if(front.getRight()!=min) //如果最小节点就是要删节点的右子节点则不改变,否则构成死循环
min.setRight(front.getRight()); //最小节点的右指针指向要删的数的右子节点
front.setLeft(null); //置空左指针
front.setRight(null); //置空有指针
if(front==behind) { //要删的是根节点
setRoot(min); //设置新的根节点
}else {
behind.setRight(min);
}
if(temp!=null&&temp!=min.getRight()) { //最小节点原本有右子树,如果最小节点的右孩子没改变就不用插入
front=min; //front原本指向要删节点,现在节点已经删除,front指向最小节点
while(front!=null) { //将原本最小节点的右子树插入到合适的位置
behind=front;
if(temp.getNum()<=front.getNum()) {
front=front.getLeft();
if(front==null)
behind.setLeft(temp);
}else {
front=front.getRight();
if(front==null)
behind.setRight(temp);
}
}
}
}else if(front.getLeft()!=null) { //要删的数有左子树,没有右子树
if(front==behind) { //要删的是根节点
front=front.getLeft(); //左移一个
behind.setLeft(null);
setRoot(front); //更新根节点
}else {
if(behind.getLeft()==front)
behind.setLeft(front.getLeft());
else
behind.setRight(front.getLeft());
}
}else { //要删的数有右子树,没有左子树
if(front==behind) {
front=front.getRight();
behind.setRight(null);
setRoot(front);
}else {
if(behind.getLeft()==front)
behind.setLeft(front.getRight());
else
behind.setRight(front.getRight());
}
}
successful=true;
}
}
if(successful)
System.out.println("删除成功");
else
System.out.println("删除失败");
return getRoot();
}
public static void main(String[] args) {
//int[] array=getArray(10);
int[] array=new int[] {24,13,43,53,72,45,41,55,18,42,46};
//int[] array=new int[] {24,18,55,41,72,80};
for(int data : array)
System.out.print(data+" ");
System.out.println();
BinarySortTree tree=new BinarySortTree();
Node root=tree.create(array);
tree.non_recursive_preOrder(root);
System.out.println();
int num,value;
boolean loop=true;
System.out.println("请输入操作:");
System.out.println("\t1.插入数据");
System.out.println("\t2.删除数据");
System.out.println("\t3.前序遍历");
System.out.println("\t4.退出");
try (Scanner scanner=new Scanner(System.in)){
while(loop) {
System.out.print("Input a number: ");
num=scanner.nextInt();
switch (num) {
case 1:
System.out.print("Input: ");
value=scanner.nextInt();
tree.add(value);
tree.non_recursive_preOrder(root);
System.out.println();
break;
case 2:
System.out.print("Input: ");
value=scanner.nextInt();
root=tree.delete(value);
tree.non_recursive_preOrder(root);
System.out.println();
break;
case 3:
tree.non_recursive_preOrder(root);
System.out.println();
break;
case 4:
loop=false;
break;
default:
break;
}
}
}
}
}
如有错误,希望大家指出(^U^)ノ~YO
