图论基础知识(四)
好像最近都挺忙的(好吧,我承认这是借口,毕竟我昨晚还在看电影和演唱会……我只是单纯的比较懒)
已经介绍了图的顶点、边、有向图、无向图、度、图的同构等知识
链接如下:
图论基础知识(一)
图论基础知识(二)
图论基础知识(三)
好了,今天想介绍的是邻接矩阵以及邻接表(先写一点,之后补充)
先放一张邻接表和邻接矩阵对比:
邻接矩阵
————————————同济第六版线性代数第27页例3——————————————
四个城市间的航线如上图所示。
若令a ij=① 1 从i市到j市有1条单向航线
② 0 从i市到j市没有单向航线
上图所示就是一个有向图
……
……
好了,回归正题
先看百度百科的定义:
邻接 矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图,其中V={v1,v2,…,vn} 。G的邻接矩阵是一个具有下列性质的n阶方阵:
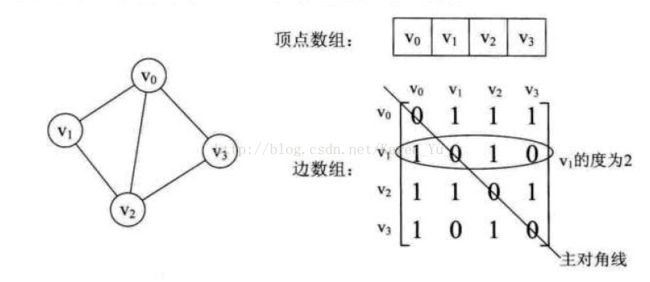
①对 无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0, 有向图则不一定如此。
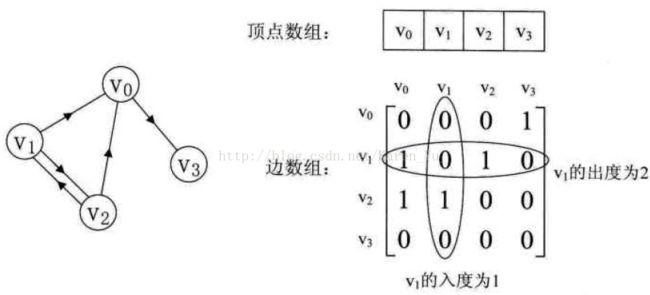
②在无向图中,任一顶点i的度为第i列(或第i行)所有非零元素的个数,在有向图中顶点i的出度为第i行所有非零元素的个数,而入度为第i列所有非零元素的个数。
③用邻接矩阵法表示图共需要n^2个空间,由于无向图的邻接矩阵一定具有 对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间。
无向图的邻接 矩阵一定是对称的,而有向图的邻接矩阵不一定对称。因此,用邻接矩阵来表示一个具有n个顶点的有向图时需要n^2个单元来存储邻接矩阵;对有n个顶点的无向图则只存入上(下)三角阵中剔除了左上右下对角线上的0元素后剩余的元素,故只需1+2+...+(n-1)=n(n-1)/2个单元。
无向图邻接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的度。
有向图邻接矩阵中第i行非零元素的个数为第i个顶点的出度,第i列非零元素的个数为第i个顶点的入度,第i个顶点的度为第i行与第i列非零元素个数之和。
用邻接矩阵表示图,很容易确定图中任意两个顶点是否有边相连。
————————————————————解释————————————————————————
上面举的例子是有向图,那么,大家想想无向图的特点是什么呢?
很简单,也就是——i市可以到j市,同样j市也可以到i市,所以自然而然的无向图的邻接矩阵一定是对称的。
见下图(无向图和有向图邻接矩阵对比——图片来自 数据结构:图的存储结构之邻接矩阵)
————————————————简而言之———————————————
邻接矩阵是用一个以0和1为元素来表示顶点与顶点之间边的关系的一种图的表示形式
代码片参考(来自 数据结构:图的存储结构之邻接矩阵):
#include
using namespace std;
#define MAXVEX 100/* 最大顶点数,应由用户定义 */
#define INFINITY 65535 /* 表示权值的无穷*/
typedef int EdgeType;/* 边上的权值类型应由用户定义 */
typedef char VertexType;/* 顶点类型应由用户定义 */
typedef struct
{
VertexType vexs[MAXVEX];/* 顶点表 */
EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */
int numNodes, numEdges;/* 图中当前的顶点数和边数 */
} MGraph;
/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *Gp)
{
int i, j, k, w;
cout << "请输入顶点数和边数(空格分隔):" << endl;
cin >> Gp->numNodes >> Gp->numEdges;
cout << "请输入顶点信息(空格分隔):" << endl;
for (i = 0; i < Gp->numNodes; i++)
cin >> Gp->vexs[i];
for (i = 0; i < Gp->numNodes; i++)
{
for (j = 0; j < Gp->numNodes; j++)
{
if (i == j)
Gp->arc[i][j] = 0;/* 顶点没有到自己的边*/
else
Gp->arc[i][j] = INFINITY;/* 邻接矩阵初始化 */
}
}
for (k = 0; k < Gp->numEdges; k++)
{
cout << "请输入边(vi, vj)的上标i,下标j和权值w(空格分隔):" << endl;
cin >> i >> j >> w;
Gp->arc[i][j] = w;
Gp->arc[j][i] = Gp->arc[i][j];/* 因为是无向图,矩阵对称 */
}
}
int main(void)
{
MGraph MG;
CreateMGraph(&MG);
return 0;
}
还有其他的代码展示,举例:http://blog.csdn.net/zhangxiangdavaid/article/details/38321327
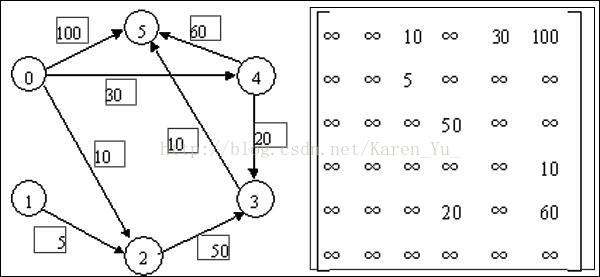
除了这种邻接矩阵,当然还有带权重的,比如:
所有不相连的就认为权重为正无穷,其他的就↑直接把每条路径上的权写上(也就不是只有0和1了——0变成了无穷,1变作权重)
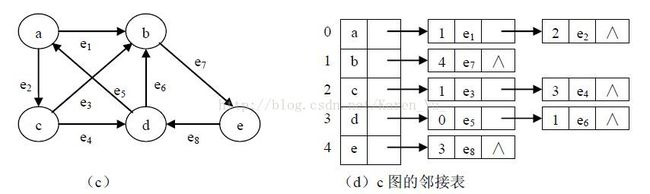
邻接表
以上图片来自网络
下面文字摘自百度百科(因为暂时这里还没怎么看懂,所以以后会接着更新的)
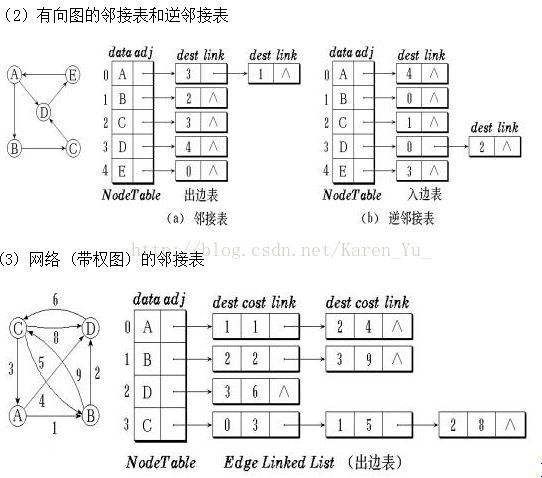
有向图
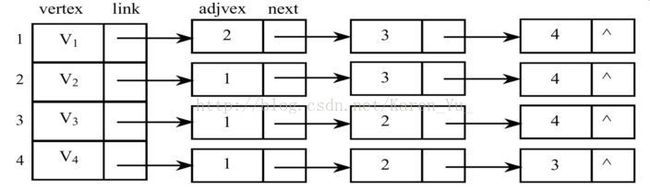
对于有向图,vi的邻接表中每个表结点都对应于以vi为始点射出的一条边。因此,将有向图的邻接表称为出边表。
【例】有向图G6如下图所示,其中顶点v1的邻接表上两个表结点中的顶点序号分别为0和4,它们分别表示从v1射出的两条边(简称为v1的出边):和。
注意:
n个顶点e条边的有向图,它的邻接表表示中有n个顶点表结点和e个边表结点。(因为有向图是单向的)
邻接表逆邻接表
在有向图中,为图中每个顶点vi建立一个入边表的方法称逆邻接表表示法。
入边表中的每个表结点均对应一条以vi为终点(即射入vi)的边。
注意:
n个顶点e条边的有向图,它的逆邻接表表示中有n个顶点表结点和e个边表结点。
邻接表是一个二维容器,第一维描述某个点,第二维描述这个点所对应的边集们。
实现邻接表的方法绝对有100种以上。即使是前向星这种东西也是邻接表,因为它还是描述某个点和这个点所对应的边集们.
我们说说常用的邻接表存图法(静态的array就不说了.)必须有开O1以及以上编译的条件,不然没有测试的效率无任何意义。
第一维是描述点的。可以用vector,list,forward_list,deque,map,multimap,unordered_map,unordered_multimap等(一般不能用set,mutiset,unordered_set,unordered_multiset).
按照你的要求去选择。一般来讲存完图以后不涉及点的加入与删除优先使用vector.map,multimap,unordered_map,unordered_multimap.
第二维是描述这个点的边集,可以用全部的容器。
也是的一般来讲存完图以后,不涉及点的加入与删除优先使用vector,空间充足可以考虑deque.涉及点的删除用forward_list或者是list,map,multimap,unordered_map,unordered_multimap.