AtCoder Grand Contest 021 B - Holes

题目链接：

AGC021B−Holes––––––––––––––––––– A G C 021 B − H o l e s _

题目大意：

简化一下题意：给 N N 个平面上的点，现在平面上任选一点放置一个机器人。这个机器人会走到离自己距离 (此距离指欧几里得距离) 最近的点，然后停下。问机器人到每个点停下的概率是多少？

数据范围：

1≤N≤100|xi|,|yi|≤106 1 ≤ N ≤ 100 | x i | , | y i | ≤ 10 6

解题思路：

先介绍一个函数— atan2() ;atan2 (y,x) ( y , x ) 返回值表示向量 (x,y) ( x , y ) 与 x x 轴正方向的夹角度数 (单位为弧度)；取值范围为 (−π,+π] ( − π , + π ] 。

先说一个比较快 (但难写) 的做法一：

先求出这 N N 个点的凸包。显然凸包里面的点是没有概率的。为什么？
如果机器人在凸包外面，显然里面的点是没有机会得；虽然机器人在凸包里的时候会有一丢丢机会，但整个平面辣么大！算出的概率相当于没有。
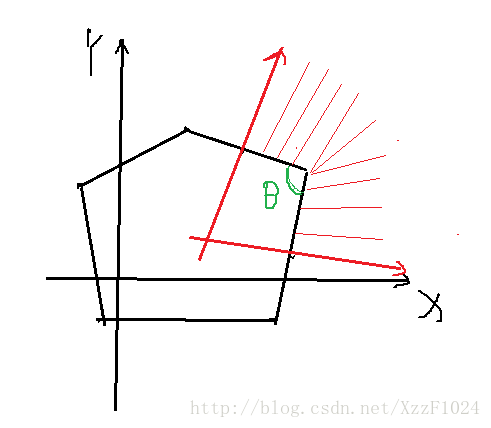
对于凸包上的一个点，令其与相邻两点所成的夹角为 θ θ ，那么这个点的概率就是 (π−θ)/2π ( π − θ ) / 2 π 。
如图所示，就是外面那片区域。(中间那一点点无关紧要)

这个做法就是求个凸包，总复杂度 O(NlogN) O ( N l o g N ) 。



再说一个比较慢 (但好写) 的做法二：

这个就要用到 atan2() 函数了！
对于一个点 s s ， 对该点到其余的点 atan2() 函数值进行排序。令相邻两个向量的夹角为 θ θ ，那么最后的答案 ans=max(θi−π,0)/2π(1≤i≤N) a n s = m a x ( θ i − π , 0 ) / 2 π ( 1 ≤ i ≤ N ) 。第 1 1 个向量和第 N N 个向量的夹角特判一下就好。
如图所示：

显然，在凸包里面的点，画一下就知道是莫得概率的。
总复杂度 O(N2logN) O ( N 2 l o g N )



做法一AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int inf = 1 << 30;
const LL INF = 1LL << 60;
const int MaxN = 105;
const double eps = 1e-6;
const double PI = acos(-1.0);

int n, top;
struct Point {
    LL x, y;
    int pos;
    double pb;
    Point () {}
    Point (LL a, LL b) {
        x = a; y = b;
    }
    bool friend operator < (const Point a, const Point b) {
        if(a.y == b.y) return a.x < b.x;
        else return a.y < b.y;
    }
    bool friend operator == (const Point a, const Point b) {
        return (a.x == b.x) && (a.y == b.y);
    }
    Point friend operator + (const Point a, const Point b) {
        return Point(a.x + b.x, a.y + b.y);
    }
    Point friend operator - (const Point a, const Point b) {
        return Point(a.x - b.x, a.y - b.y);
    }
}PP[MaxN + 5];
Point hull[MaxN + 5];               //存放凸包的数组

typedef Point Vector;               //向量和点一样,都有x、y元素,所以这里就偷了个懒

LL Dis(Point A, Point B) {
    return (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y);
}

double dis(Point A, Point B) {      //两点的距离
    return sqrt(1.0 * Dis(A, B));
}

LL Cross(Vector A, Vector B) {     //叉积
    return A.x * B.y - A.y * B.x;
}

bool Gcmp(Point A, Point B) {       //按照极角从大到小排序
    Point O = PP[1];                //最下方的点一定在凸包上,将其作为原点进行极角排序
    LL tmp = Cross(A - O, B - O);
    //向量OA和OB的叉积
    //其实也可以直接写成Cross(A - O, B - O),那样写只是为了便于理解

    if(tmp == 0) {                  //叉积为0,共线;所以离原点近的排在前面
        if(Dis(A, O) < Dis(B, O)) return true;
        else return false;
    }
    else {                          //不为0,不共线
        if(tmp > 0) return true;    //大于0,说明向量OB在向量OA的左边,所以OA排在前面
        else return false;          //反之,OB排在前面
    }
}

void Graham() {                     //求凸包
    sort(PP + 1, PP + n + 1);       //排序找出最下方的点,作为原点
    sort(PP + 2, PP + n + 1, Gcmp); //对其余的点进行极角排序
    hull[1] = PP[1];
    hull[2] = PP[2];
    top = 2;
    for(int i = 3; i <= n; i++) {
        while(top >= 2 && Cross(hull[top] - hull[top - 1], PP[i] - hull[top - 1]) < 0)
            top--;
        hull[++top] = PP[i];
    }
}

bool Pcmp(Point A, Point B) {
    return A.pos < B.pos;
}

void debug() {
    printf("top = %d\n", top);
    for(int i = 1; i <= top; i++)
        printf("%d %d\n", hull[i].x, hull[i].y);
    printf("\n");
}

double prod(Vector A, Vector B) {
    return 1.0 * (A.x * B.x + A.y * B.y);
}

void solve() {
    hull[0] = hull[top];
    hull[top + 1] = hull[1];
    for(int i = 1; i <= top; i++) {
        Vector sa = hull[i - 1] - hull[i];
        Vector sb = hull[i + 1] - hull[i];
        hull[i].pb = (PI - acos(prod(sa, sb) / (dis(sa, Point(0LL, 0LL)) 
                         * dis(sb, Point(0LL, 0LL))))) / (2.0 * PI);
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= top; j++) {
            if(PP[i] == hull[j]) {
                PP[i].pb = hull[j].pb;
                break;
            }
        }
    }
    sort(PP + 1, PP + n + 1, Pcmp);
    for(int i = 1; i <= n; i++)
        printf("%.15lf\n", PP[i].pb);
}

int main()
{
    //printf("acos() = %lf\n", acos(-0.5));
    while(scanf("%d", &n) != EOF)
    {
        top = 0;
        for(int i = 1; i <= n; i++) {
            scanf("%lld %lld", &PP[i].x, &PP[i].y);
            PP[i].pos = i;
            PP[i].pb = 0.0;
        }
        Graham();
        //debug();
        solve();
    }
    return 0;
}

做法二AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int inf = 1 << 30;
const LL INF = 1LL << 60;
const int MaxN = 105;
const double eps = 1e-6;
const double PI = acos(-1.0);

int n;
struct Point {
    int x, y;
}PP[MaxN + 5];

double slope[MaxN + 5];

int main()
{
    //printf("%lf\n", atan2(0, 1));
    while(scanf("%d", &n) != EOF) 
    {
        for(int i = 1; i <= n; i++) scanf("%d %d", &PP[i].x, &PP[i].y);
        for(int i = 1; i <= n; i++) {
            int tot = 0;
            for(int j = 1; j <= n; j++)
                if(i != j)
                    slope[++tot] = atan2(PP[j].y - PP[i].y, PP[j].x - PP[i].x);
            sort(slope + 1, slope + tot + 1);
            double ans = 0.0;
            ans = max(ans, PI - (slope[tot] - slope[1]));
            for(int j = 2; j <= tot; j++) 
                ans = max(ans, (slope[j] - slope[j - 1]) - PI);
            printf("%.10lf\n", ans / (2 * PI));
        }
    }
    return 0;
}

对于这种情况，我显然选择做法二。 哈哈哈哈！