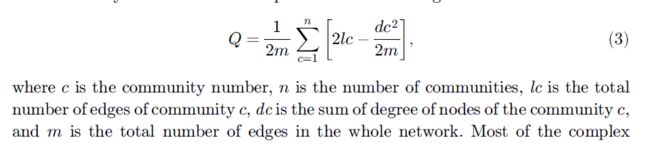社区发现的3个评估指标：标准化互信息NMI，ARI指标，以及模块度（modularity）...

转载请注明出处：http://www.cnblogs.com/bethansy/p/6890972.html

一、已知真实社区划分结果

1.NMI指数，互信息和标准化互信息

 

 

    具体公式和matlab代码参见博客，Python代码参加，C++代码参见

function MIhat = nmi( A, B )
%NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% Author: http://www.cnblogs.com/ziqiao/   [2011/12/15] 

if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
end
if iscolumn(A)
    A=A';
end
if iscolumn(B)
    B=B';
end
total = length(A);
A_ids = unique(A);
A_class = length(A_ids);
B_ids = unique(B);
B_class = length(B_ids);
% Mutual information
idAOccur = double (repmat( A, A_class, 1) == repmat( A_ids', 1, total )); %得到节点社区矩阵N*C
idBOccur = double (repmat( B, B_class, 1) == repmat( B_ids', 1, total ));
idABOccur = idAOccur * idBOccur';
Px = sum(idAOccur') / total;
Py = sum(idBOccur') / total;
Pxy = idABOccur / total;
MImatrix = Pxy .* log2(Pxy ./(Px' * Py)+eps);
MI = sum(MImatrix(:));
% Entropies
Hx = -sum(Px .* log2(Px + eps),2);
Hy = -sum(Py .* log2(Py + eps),2);
%Normalized Mutual information
MIhat = 2 * MI / (Hx+Hy);


% MIhat = MI / sqrt(Hx*Hy); another version of NMI

end

　重叠社区NMI指数可参照博客

2.ARI指数

文献来源：【2015浙江大学博士】复杂网络节点影响力模型及其应用_王益文

       ARI原理介绍，ARI ＭＡＴＬＡＢ代码下载　，ARI评估指数包含在EDA工具箱中，EDA工具箱介绍

   ARI的评估函数在EDA的工具箱中，调用函数甚多，就不贴出来了。自己下载EDA工具箱，放在matlab\toolbox文献夹下，设置完路径即可调用adjrand()

二、不知道真实社区划分情况

1.模块度Q（社区内的边尽可能多，而社区之间的边尽量地少）

 

 

     Q就是模块度，模块度越大则表明社区划分效果越好。Q值的范围在[-0.5,1），论文表示当Q值在0.3~0.7之间时，说明聚类的效果很好

具体推导流程参见博客，这篇博客推导流程非常详细，而且使用矩阵运算减少了运算复杂度。

    代码如下，A是图的邻接矩阵， a是n*1的向量,即每个节点所属社区。例如[1 2 1 1 2],表示节点1、3、4属于社区1，节点2、5属于社区5

 

function [Q1]=modul(A,a)
one = 1:length(A);
a = [one' a];
% 　建立节点社区矩阵
a = accumarray(a,1);
a = a(:,any(a));%　 删除A中全0的列
% 　进行网络A模块度Ｑ1运算
m = sum(sum(A))/2;
k = sum(A,2);
B = A - (repmat(k,[1,size(A,1)]) .* repmat(k',[size(A,1),1])) / (2*m);
Q1 = 1/(2*m) .* trace(a'*B*a);
end

　　

 

转载于:https://www.cnblogs.com/bethansy/p/6890972.html