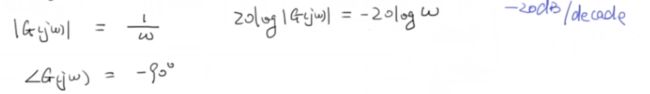如何理解信号处理/自控原理中的bode图,并分析系统?
bode图实际上描述的就是系统的频率响应,首先对画系统频率响应的方法进行讨论。
滤波器频率响应
下面代码给出了怎么去画滤波器的频率响应(幅频和相频曲线),以及滤波的方法。
clear, close all
%% initialize parameters
% 载波频率
samplerate = 1000; % in Hz 采样率
N = 512; % number of points, must be even, better be power of 2
%% define a and b coeffients of H (transfer function)
a = [1 -0.2 0.8]; % denominator terms
b = [0.2 0.5 0]; % numerator terms
%% 或者下面:
N = 512;
[h1 , ftp] = freqz(b,a,N,samplerate);
mag = 20*log10(abs(h1)); % get magnitude of spectrum in dB
phase = angle(h1)/pi*180; % get phase in deg.
figure,
subplot(2,1,1),semilogx(ftp,mag)
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
grid on
subplot(2,1,2),semilogx(ftp,phase,'r')
xlabel('Frequency (Hz)'),ylabel('Phase (deg.)')
grid on
%% 信号滤波
acc_magFilt = filtfilt(b, a, acc_magFilt);
给信号滤波的过程中,需要注意幅频响应。如果在带通范围内不是1的话,就会改变信号的幅值,就会改变最终加速度输出的信号。另外,上面的图就是bode图,但是是基于离散系统的。
上面是一个离散系统,对于一个连续系统,可以直接调用bode(b,a)就可以画出传递函数的bode图了。
如何去理解bode图?
总结来说有以下几点:
- 振幅的比较用10log10就行,但是能量的比较需要20log10
- 振幅与功率/能量之间的关系如下:
从一个实例出发理解bode图
对于系统传递函数:
G ( s ) = a s + a G(s)=\frac{a}{s+a} G(s)=s+aa
分析频率响应:
∣ G ( j ω ) ∣ = 1 1 + ( ω a ) 2 |G(j \omega)|=\sqrt{\frac{1}{1+\left(\frac{\omega}{a}\right)^{2}}} ∣G(jω)∣=1+(aω)21
∠ G ( j ω ) = − arctan ( w a ) \angle G(j \omega)=-\arctan \left(\frac{w}{a}\right) ∠G(jω)=−arctan(aw)
- 低频:w<
∣ G ( j ω ) ∣ = 1 20 log ∣ G ( j ω ) ∣ = 0 ∠ G ( j ω ) = 0 \begin{array}{l} | G(j \omega)| = 1\\ 20 \log|G(j \omega)|=0 \\ \angle G(j \omega)=0 \end{array} ∣G(jω)∣=120log∣G(jω)∣=0∠G(jω)=0
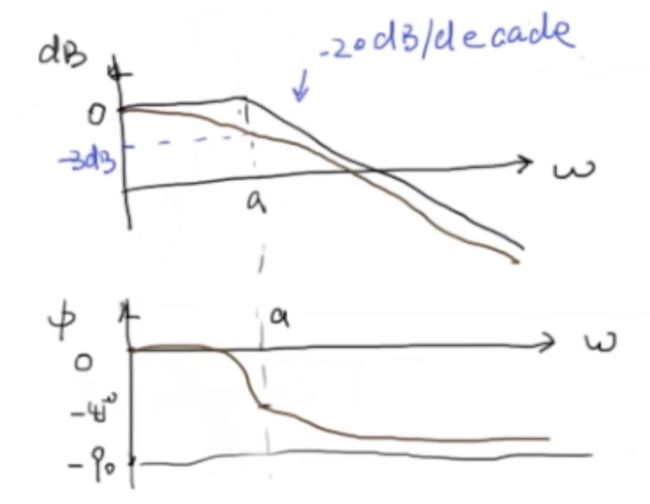
- 截止频率:w=a
这个-3dB很重要,表达的是输出的振幅是输入的振幅的sqrt(1/2),能量是一半的关系。
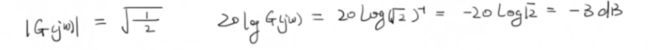
∠ G ( g w ) = − arctan 1 = − 4 5 ∘ \angle G(g w)=-\arctan 1=-45^{\circ} ∠G(gw)=−arctan1=−45∘
- 高频:w>>a
bode图如下:
bode图的作用是什么?
实际上,我们可以将级联系统的子系统bode图进行累加,那么我们就得到了新的级联系统的真正的bode图了。原理如上。