LeetCode-5406、收集树上所有苹果的最少时间-中等
LeetCode-5406、收集树上所有苹果的最少时间-中等
给你一棵有 n 个节点的无向树,节点编号为 0 到 n-1 ,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从 节点 0 出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。
无向树的边由 edges 给出,其中 edges[i] = [fromi, toi] ,表示有一条边连接 fromi 和 toi 。除此以外,还有一个布尔数组 hasApple ,其中 hasApple[i] = true 代表节点 i 有一个苹果,否则,节点 i 没有苹果。
示例 1:
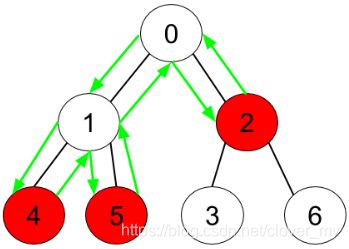
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
输出:8
解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 2:
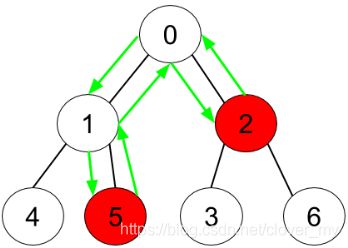
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
输出:6
解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 3:
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
输出:0
提示:
- 1 <= n <= 10^5
- edges.length == n-1
- edges[i].length == 2
- 0 <= fromi, toi <= n-1
- fromi < toi
- hasApple.length == n
代码:
class Solution:
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
dic = {0: [0]}
for a, b in edges:
dic[b] = dic[a] + [b]
paths = []
rng = 0
for k, v in dic.items():
if hasApple[k]:
paths.append(v)
rng = max(rng, len(v))
if not paths:
return 0
ans = 0
for i in range(1, rng):
s = []
for p in paths:
if i < len(p) and p[i] not in s:
s.append(p[i])
ans += len(s) * 2
return ans