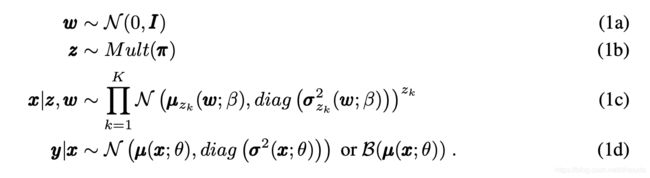深度学习（生成式模型GMVAE）——deep unsupervised clustering with gaussian mixture variational autoencoders

前言

我将看过的论文建了一个github库，方便各位阅读地址

传统的VAE，隐变量服从标准高斯分布（单峰），但有时候，单个高斯分布可能不能完全表达图像x的特征，比如MINIST数据集有0~9这10个数字，直觉上使用10个高斯分布来替代单个高斯分布更为合理，因此有学者将混合高斯分布模型（GMM）与VAE进行结合，其结果便是GMVAE。

FBI warning
本文为代码与论文结合进行理解的产物，如有错误，欢迎指出。本文不会进行ELBO的推导，将直接从论文给出的ELBO算式进行讲解。

GMVAE的生成过程

生成步骤如下：

说人话就是：

1. 1a表示从标准正态分布中进行采样，得到$w$，具体的采样方法我会写一篇博客进行说明
2. 1b表示从Mult分布中采样$z=[z_1,z_2,...z_K]$，$z$其实是一个one-hot编码，其实可以自己随意指定
3. 由于$z_k$的取值非0即1，而$A^0=1$，所以1c表示从GMM中选择一个高斯分布进行采样，得到隐变量x，GMM中每个高斯分布的均值和方差将由步骤一采样到的$w$进行变化得到，K为高斯分布个数
4. 1d表示利用隐变量x生成图像y，由Decoder完成

GMVAE的损失函数

损失函数由变分推断推导而来，由于论文遗漏了太多推导细节，本文将不会介绍这部分推导，将重点介绍损失函数的各个部分如何计算。

与VAE一样，GMVAE通过最大化ELBO来进行优化，ELBO的形式如下：

$$\begin{array}{rl}{L}_{ELBO}=& E_{q(x|y)}[p_{\theta }(y|x)]-E_{q(w|y)p(z|x,w)}[KL(q_{{\varphi }_x}(x|y)||p_{\beta }(x|w,z))]\\ & -KL(q_{{\varphi }_x}(w|y)||p(w))-E_{q_{(}x|y)q(w|y)}[KL(p_{\beta }(z|x,w)||p(z))]\end{array}$$

${\varphi }_x、\theta 、\beta$表示待优化的参数，可以暂时忽视。

• $E_{q(x|y)}[p_{\theta }(y|x)]$称为reconstruction term
• $E_{q(w|y)p(z|x,w)}[KL(q_{{\varphi }_x}(x|y)||p_{\beta }(x|w,z))]$表示conditional prior term
• $KL(q_{{\varphi }_x}(w|y)||p(w))$表示w-prior term
• $E_{q_{(}x|y)q(w|y)}[KL(p_{\beta }(z|x,w)||p(z))]$表示z-prior term

接下来我将介绍每一部分的计算方式

reconstruction term

$E_{q(x|y)}[p_{\theta }(y|x)]$表示重构误差，由于我们假定$p_{\theta }(y|x)$服从高斯分布，所以与VAE一样，可以用均方误差进行计算。

conditional prior term

对$E_{q(w|y)p(z|x,w)}[KL(q_{{\varphi }_x}(x|y)||p_{\beta }(x|w,z))]$使用蒙特卡洛模拟，可得

$$\frac{1}{M}\sum _{j=1}^M\sum _{k=1}^K{p}_{\beta }(z_k=1|x^{(j)},w^{(j)})KL(q_{{\varphi }_x}(x|y)||p_{\beta }(x|w^{(j)},z_k=1))\text{\hspace{1em}(1.0)}$$

$M$采样的样本数，我们可以将其设置为1，则1.0可变化为

$$\begin{array}{rl}& \sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)KL(q_{{\varphi }_x}(x|y)||p_{\beta }(x|w,z_k=1))\\ =& \sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)E_{q_{{\varphi }_x}(x|y)}[\log \frac{q_{{\varphi }_x}(x|y)}{p_{\beta }(x|w,z_k=1)}]\\ =& \sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\sum _{i=1}^N\log \frac{q_{{\varphi }_x}(x_i|y)}{p_{\beta }(x_i|w,z_k=1)}\end{array}\text{\hspace{1em}(2.0)}$$

第三行式子利用蒙特卡洛模拟得到，同理，将N设置为1，式2.0可变为
$$\begin{array}{rl}& \sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\log \frac{q_{{\varphi }_x}(x|y)}{p_{\beta }(x|w,z_k=1)}\\ =& \sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\log q_{{\varphi }_x}(x|y)-\sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\log p_{\beta }(x|w,z_k=1)\\ =& \log q_{{\varphi }_x}(x|y)-\sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\log p_{\beta }(x|w,z_k=1)\end{array}\text{\hspace{1em}(3.0)}$$

$K$为混合高斯分布中高斯分布的个数，我们有如下假设：

• $q_{{\varphi }_x}(x|y)$是一个多元高斯分布，其期望与方差为${\mu }^{{\varphi }_x}$、$({\delta }^{{\varphi }_x}{)}^2$。为方便书写与做图，本文将用一元高斯分布形式进行推导，请读者自行将推导结果中的期望与方差替换为多元高斯分布形式。
• 依据式1c，$\log p_{\beta }(x|w,z_k=1)$是均值为${\mu }_k^{\beta }$，方差为$({\delta }_k^{\beta }{)}^2$的多元高斯分布

则有
$$\begin{array}{rl}\log p_{\beta }(x|w,z_k=1)& =\log \frac{1}{\sqrt{2\pi }{\delta }_k^{\beta }}{e}^{-\frac{(x-{\mu }_k^{\beta }{)}^2}{2({\delta }_k^{\beta }{)}^2}}\\ & =\log \frac{1}{\sqrt{2\pi }}-\log {\delta }_k^{\beta }-\frac{(x-{\mu }_k^{\beta }{)}^2}{2({\delta }_k^{\beta }{)}^2}\end{array}\text{\hspace{1em}(4.0)}$$

$$\begin{array}{rl}\log q_{{\varphi }_x}(x|y)& =\log \frac{1}{\sqrt{2\pi }{\delta }^{{\varphi }_x}}{e}^{-\frac{(x-{\mu }^{{\varphi }_x}{)}^2}{2({\delta }^{{\varphi }_x}{)}^2}}\\ & =\log \frac{1}{\sqrt{2\pi }{\delta }^{{\varphi }_x}}{e}^{-\frac{(x-{\mu }^{{\varphi }_x}{)}^2}{2({\delta }^{{\varphi }_x}{)}^2}}\\ & =\log \frac{1}{\sqrt{2\pi }}-\log {\delta }^{{\varphi }_x}-\frac{(x-{\mu }^{{\varphi }_x}{)}^2}{2({\delta }^{{\varphi }_x}{)}^2}\end{array}\text{\hspace{1em}(5.0)}$$

$x$是服从$q_{{\varphi }_x}(x|y)$分布的样本，可以通过VAE提出的reparameterization trick得到

w-prior term

$KL(q_{{\varphi }_x}(w|y)||p(w))$有如下假设

• $q_{{\varphi }_x}(w|y)$服从期望为$[{\mu }_1^{{\varphi }_w}、{\mu }_2^{{\varphi }_w}......{\mu }_n^{{\varphi }_w}]$，方差为$[({\delta }_1^{{\varphi }_w}{)}^2、({\delta }_2^{{\varphi }_w}{)}^2......({\delta }_n^{{\varphi }_w}{)}^2]$的独立多元高斯分布
• $p(w)$服从标准正态分布

则有
$$\begin{array}{r}KL(q_{{\varphi }_x}(w|y)||p(w))=\frac{1}{2}\sum _{i=1}^n(({\mu }_i^{{\varphi }_w}{)}^2+({\delta }_i^{{\varphi }_w}{)}^2-1-\log ({\delta }_i^{{\varphi }_w}{)}^2)\end{array}\text{\hspace{1em}(6.0)}$$

z-prior term

同理，对$E_{q_{(}x|y)q(w|y)}[KL(p_{\beta }(z|x,w)||p(z))]$使用蒙特卡洛模拟，可得

$$\frac{1}{M}\sum _{i=1}^{M}KL(p_{\beta }(z|x_i,w_i)||p(z))$$

我们有如下假设

• p(z)为均匀分布，设$p(z)=\frac{1}{K}$，$K$为混合高斯分布中高斯分布的个数

将M设置为1，则有

$$\begin{array}{rl}KL(p_{\beta }(z|x,w)||p(z))& =\sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)\log \frac{p_{\beta }(z_k=1|x,w)}{p(z_k=1)}\\ & =\sum _{k=1}^K{p}_{\beta }(z_k=1|x,w)[\log p_{\beta }(z_k=1|x,w)+\log K]\end{array}$$

GMVAE的结构

本节结构为博主阅读代码后所得，博主没有复现GMVAE，故仅供参考。

代码地址

图像生成的结构如下

如果您想了解更多有关深度学习、机器学习基础知识，或是java开发、大数据相关的知识，欢迎关注我们的公众号，我将在公众号上不定期更新深度学习、机器学习相关的基础知识，分享深度学习中有趣文章的阅读笔记。