第14章 概率图模型--近似推断

精确推断方法通常需要很大的计算开销，因此在现实应用中近似推断方法更为常用。近似推断方法大致可分为两大类：第一类是采样（sampling），通过使用随机化方法完成近似；第二类是使用确定性近似完成近似推断，典型代表为变分推断（variational inference）。

1 MCMC采样

在很多任务中，我们关心某些概率分布并非因为对这些概率分布本身感兴趣，而是要基它们计算某些期望，并且还能进一步基于这些期望做出决策。例如对图7（a）的贝叶斯网，进行推断的目的可能是为了计算变量 x5 的期望。若直接计算或逼近这个期望比推断概率分布更容易，则直接操作无疑将使推断问题的求解更为高效。
采样法正是基于这个思路。具体来说，假定我们的目标是计算函数 f(x) 在概率密度函数 p(x) 下的期望

Ep[f]=∫f(x)p(x)dx（21）

则可根据 p(x) 抽取一组样本 {x1,x2,...,xn} ，然后计算 f(x) 在这些样本上的均值

f^=1N∑i=1Nf(xi)（22）

以此来近似目标期望 Ep[f] 。若样本 {x1,x2,...,xn} 独立，基于大数定律，这种通过大量采样的办法就能获得较高的近似精度。问题的关键是如何采样。对概率图模型来说，就是如何高效地基于图模型所描述的概率分布来获取样本。
概率图模型中最常用的采样技术是马尔可夫链蒙特卡罗（Markov Chain Monte Carlo，简称MCMC）方法。给定连续变量 x∈X 的概率密度函数 p(x) ， x 在区间 A 中的概率可计算为

P(A)=∫Ap(x)dx（23）

若有函数： f:X↦R ，则可计算 f(x) 的期望

p(f)=Ep[f(x)]=∫xf(x)p(x)dx（24）

若 x 不是单变量而是一个高维多元变量 x ，且服从一个非常复杂的分布，则对式（24）求积分通常很困难。为此，MCMC先构造出服从 p 分布的独立同分布随机变量 x1,x2,...,xn ，再得到式（24）的无偏估计

p˜(f)=\fra1N∑i=1Nf(xi)（25）

然而，若概率密度函数 p(x) 很复杂，则构造服从 p 分布的独立同分布样本也很困难。MCMC方法的关键就在于通过构造“平稳分布为 p 的马尔可夫链”来产生样本：若马尔可夫链运行时间足够长（即收敛到平稳状态），则此时产出的样本 x 近似服从于分布 p 。如何判断马尔可夫链达到平稳状态呢？假定平稳马尔可夫链 T 的状态转移概率（即从状态 x 转移到状态 x′ 的概率）为 T(x′|x) ， t 时刻状态的分布为 p(xt) ，则若在某个时刻马尔可夫链满足平稳条件

p(xt)T(xt−1|xt)=p(xt−1T(xt)|xt−1),（26）

则 p(x) 是该马尔可夫链的平稳分布，且马尔可夫链在满足该条件时已收敛到平稳状态。
也就是说，MCMC方法先设法构造一条马尔可夫链，使其收敛至平稳分布恰为待估计参数的后验分布，然后通过这条马尔可夫链来产生符合后验分布的样本，并基于这些样本来进行估计。这里马尔可夫链转移概率的构造至关重要，不同的构造方法将产生不同的MCMC算法。
Metropolis-Hastings（简称MH）算法是MCMC的重要代表。它基于“拒绝采样”（reject sampling）来逼近平稳分布 p 。如图9所示，算法每次根据上一轮采样结果 xt−1 来采样获得候选状态样本 x∗ ，但这个候选样本会以一定的概率被“拒绝”掉。假定从状态 xt−1 到状态 x∗ 的转移概率为 Q(x∗|xt−1)A(x∗|xt−1) ，其中 Q(x∗|xt−1) 是用户给定的先验概率， A(x∗|xt−1) 是 x∗ 被接受的概率。若 x∗ 最终收敛到平稳状态，则根据式（26）有

p(xt−1)Q(x∗|xt−1)A(x∗|xt−1)=p(x∗)Q(xt−1|x∗)A(xt−−1|x∗),（27）

Metropolis-Hastings算法

---

输入：先验概率 Q(x∗|xt−1) .
过程：
1：初始化 x0 ;
2： for t=1,2,... do
3：根据 Q(x∗|xt−1) 采样出候选样本 x∗ ;
4：根据均匀分布从 (0,1) 范围内采样出阈值 u ;
5： if u≤A(x∗|xt−1) then
6： xt=x∗
7： else
8： xt=xt−1
9： end if
10： end for
11： return x1,x2,...

---

于是，为了达到平稳状态，只需将接受率设置为

A(x∗|xt−1)=min(1,p(x∗)Q(xt−1|x∗)p(xt−1)Q(x∗|xt−1))（28）

吉布斯采样（Gibbs sampling）有时被视为MH算法的特例，它也使用马尔可夫链获取样本，而该马尔可夫链的平稳分布也是采样的目标分布 p(x) 。具体来说，假定 x={x1,x2,...,xn} ，目标分布为 p(x) ，在初始化 x 的取值后，通过循环执行以下步骤来完成采样：
（1）随机或以某个次序选取某个变量 xi ;
（2）根据 x 中除 xi 外的变量的现有取值，计算条件概率 p(xi|xi¯) ，其中 xi¯={x1,x2,...,xi−1,xi+1,...,xn} ;
（3）根据 p(xi|xi¯) 对变量 xi 采样，用采样值代替原值。

2 变分推断

变分推断通过使用已知简单分布来逼近需推断的复杂分布，并通过限制近似分布的类型，从而得到一种局部最优、但具有确定解的近似后验分布。
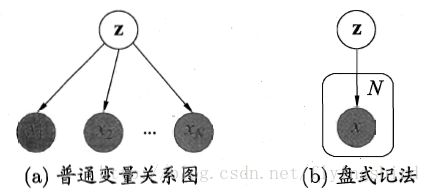
在学习变分推断之前，我们先介绍概率图模型一种简洁的表示方法–盘式标记法（plate notation）[Buntine,1994]。图10给出了一个简单的例子。图10（a）表示 N 个变量 x1,x2,...,xn} 均依赖于其他变量 z 。在图10（b）中，相互对立的、由相同机制生成的多个变量被放在一个方框（盘）内，并在方框中标出类似变量重复出现的个数 N ；方框可以嵌套。通常用阴影标注出已知的、能观察到的变量，如图（10）中的变量 x 。在很多学习任务中，对属性变量使用盘式记法将使得图表示非常简洁。
图10 盘式记法的例示

在图10（b）中，所有能观察到的变量 x 的联合分布的概率密度函数是

p(x|θ)=πNi=1∑zp(xi,z|θ),（29）

所对应的对数似然函数为

lnp(x|θ)=∑i=1Nln{∑zp(xi,z|θ)},（30）

其中 x={x1,x2,...,xn},θ 是 x 与 z 服从的分布参数。
一般来说，图10所对应的推断和学习任务主要是由观察到的变量 x 来估计隐变量 z 和分布参数变量 θ ，即求解 p(z|x,θ) 和 θ 。
概率模型的参数估计通常以最大化对数似然函数为手段。对式（30）可使用EM算法：在E步，根据 t 时刻的参数 θt 对 p(z|x,θt) 进行推断，并计算联合似然函数 p(x,z|θ) ；在M步，基于E步的结果进行最大化寻优，即对关于变量 θ 的函数 Q(θ;θt) 进行最大化从而求取

θt+1=argmaxQ(θ;θt)=argmax∑zp(z|x,θt)lnp(x,z|θ)（31）

式（31）中的 Q(θ;θt) 实际上是对数联合似然函数 lnp(x,z|θ) 在分布 p(z|x,θt) 下的期望，当分布 p(z|x,θt) 与变量 z 的真实后验分布相等时， Q(θ;θt) 近似于对数似然函数。于是，EM算法最终可获得稳定的参数 θ ，而隐变量 z 的分布也能通过该参数获得。
需注意的是， p(z|x,θt) 未必是隐变量 z 服从的真实分布，而只是一个近似分布。若将这个近似分布用 q(z) 表示，则不难验证

lnp(x)=L(q)+KL(q||p),（32）

其中

L(q)=∫q(z)ln{p(x,z)q(z)}dz(33)

KL(q||p)=−∫q(z)lnp(z|x)q(z)dz(34)

然而在现实任务中，E步对 p(z|x,θt) 的推断很可能因 z 模型复杂而难以进行，此时可借助变分推断。通常假设 z 服从分布

q(z)=∏i=1Mqi(zi),（35）

即假设复杂的多变量 z 可拆解为一系列相互独立的多变量 zi 。更重要的是，可以令 qi 分布相对简单或有很好的结构，例如假设 qi 为指数族（exponential family）分布，此时有

L(q)=∫∏iqi{lnp(x,z)−∑ilnqi}dz=∫qj{∫lnp(x,z)∏i≠jqidzi}dzj−∫qjlnqjdzj+const=∫qjlnp˜(x,zj)dzj−∫qjlnqjdzj+const,（36）

其中

lnp˜(x,zj)=Ei≠j[lnp(x,z)]+const,（37）

Ei≠j[lnp(x,z)]=∫lnp(x,z)∏i≠jqidzi.（38）

我们关心的是 qj ，因此可固定 qi≠j 再对 L(q) 进行最大化，可发现式（36）等于 −KL(qj||∏p(x,zj)) ，即当 qj=∏p(x,zj) 时 L(q) 最大。于是可知变量子集 zj 所服从的最优分布 q∗j 应满足

lnq∗j(zj)=Ei≠j[lnp(x,z)]+const,（39）

即

q∗j(zj)=exp(Ei≠j[lnp(x,z)])∫exp(Ei≠j[lnp(x,z)])dzj.（40）

换言之，在式（35）这个假设下，变量子集 zj 最接近真实情形的分布由式（40）给出。
显然，基于式（35）的假设，通过恰当地分割独立变量子集 zj 并选择 qi 服从的分布， Ei≠j[lnp(x,z)] 往往有闭式解，这使得基于式（40）能高效地对隐变量 z 进行推断。事实上，由式（38）可看出，对变量 zj 分布 q∗j 进行估计时融合了 zj 之外的其他 zi≠j 的信息，这是通过联合似然函数 lnp(x,z) 在 zj 之外的隐变量分布上求期望得到的，因此亦称“平均场（mean field）”方法。
在实践中使用变分法时，最重要的是考虑如何对隐变量进行拆解，以及假设各种变量子集服从何种分布，在此基础上套用式（40）的结论再结合EM算法即可进行概率图模型的推断和参数估计。显然，若隐变量的拆解或变量子集的分布假设不当，将会导致变分法效率低、效果差。