gmoj 5058. 【GDSOI2017模拟4.13】采蘑菇 O(n)做法

Time Limits: 2000 ms
Memory Limits: 262144 KB

题目

Description

A君住在魔法森林里，魔法森林可以看做一棵n个结点的树，结点从1~n编号。树中的每个结点上都生长着蘑菇。蘑菇有许多不同的种类，但同一个结点上的蘑菇都是同一种类，更具体地，i号结点上生长着种类为c[i]的蘑菇。
现在A君打算出去采蘑菇，但他并不知道哪里的蘑菇更好，因此他选定起点s后会等概率随机选择树中的某个结点t作为终点，之后从s沿着(s,t)间的最短路径走到t.并且A君会采摘途中所经过的所有结点上的蘑菇。
现在A君想知道，对于每一个结点u，假如他从这个结点出发，他最后能采摘到的蘑菇种类数的期望是多少。为了方便，你告诉A君答案*n的值即可。

Input

第一行一个整数n表示结点数。
第二行n个整数c[i]表示每个结点的蘑菇的种类。
接下来n-1行每行两个数u[i],v[i]表示树中的一条边。

Output

输出n行每行一个整数，第i行的整数表示起点为结点i时的答案。

Sample Input

5
1 2 3 2 3
1 2
1 3
2 4
2 5

Sample Output

10
9
12
9
11

Data Constraint

30%的数据：n <= 2000
另有20%的数据：给出的第i条边为{i,i+1}
另有20%的数据：蘑菇的种类最多3种
100%的数据：1 <= n <= 3*10^5 , 0 <= c[i] <= n

---

题解

这题可以用点分治或换根+线段树来做，这两种做法都是$O(n\log n)$的（听说还可以用虚树做）。但是，一位dalao却想出了一种巧妙的$O(n)$做法。

不妨把这棵树看成一个有根树。先定义几个量，令siz[x]表示以x为根的子树的大小，up[x]表示x到根的路径上离x最近的、父亲节点颜色为$c_x$的点的编号，sum[x]表示up值为x的点的siz总和，如下图所示（黑色的点表示颜色相同的点）：

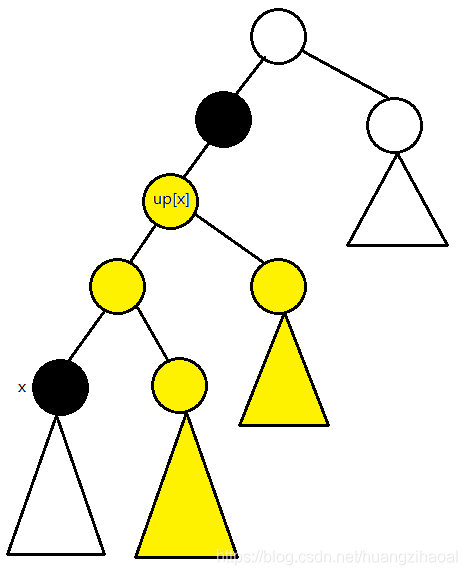
考虑颜色$c_x$对那堆黄色点（黄色点的颜色不一定相同）的答案的贡献，发现从那堆黄色点出发，经过颜色$c_x$的路径有2种：第一种是向上走经过$f{a}_{u{p}_x}$的路径，这样的贡献是$n-si{z}_{u{p}_x}$；第二种是向下走经过点x的路径，这样的贡献是$su{m}_{u{p}_x}$。因此，对于一个点x，它对黄色点的两种贡献的总和为$n-si{z}_x+su{m}_x$。因为$u{p}_x$对在x的子树里的点的答案没有贡献，所以在计算以x为根的子树的答案时，要减去$n-si{z}_{u{p}_x}+su{m}_{u{p}_x}$

考虑特殊情况。当节点x没有up时，如下图所示：

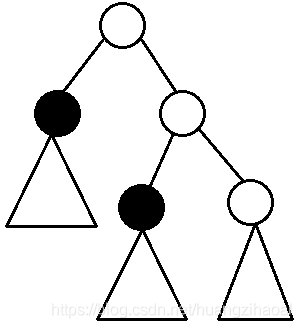
显然，若一个点x到根的路径中不包含黑色节点，可以获得所有以没有up的黑色节点为根的子树的大小的贡献，但是其他子树不能获得这个贡献。此外，还没有考虑起点的颜色贡献，因此答案要加上n。

实现的时候建议用dfs序把树转化成一个序列，然后用差分处理。
这种方法打起来是不是简单又自然？

CODE

#include
using namespace std;
#define ll long long
#define M 600005
#define N 300005
int fir[N],to[M],nex[M],c[N],b[N],siz[N],up[N],dfn[N],las[N],next[N],n,s,cnt;
ll ans[N],tag[N],sum[N];
inline char gc()
{
	static char buf[100005],*l=buf,*r=buf;
	return l==r&&(r=(l=buf)+fread(buf,1,100005,stdin),l==r)?EOF:*l++;
}
inline void read(int &x)
{
	char ch;
	while(ch=gc(),ch<'0'||ch>'9');x=ch-48;
	while(ch=gc(),ch>='0'&&ch<='9') x=x*10+ch-48;
}
inline void inc(int x,int y)
{
	to[++s]=y,nex[s]=fir[x],fir[x]=s;
	to[++s]=x,nex[s]=fir[y],fir[y]=s;
}
inline void modify(int u,int v,int num){tag[u]+=num,tag[v+1]-=num;}
void dfs(int k,int from)
{
	int i,tmp=b[c[k]];
	up[k]=tmp,dfn[k]=++cnt,siz[cnt]=1;
	for(i=fir[k];i;i=nex[i])
		if(to[i]!=from)
		{
			b[c[k]]=cnt+1,dfs(to[i],k);
			siz[dfn[k]]+=siz[dfn[to[i]]];
		}
	b[c[k]]=tmp;
	sum[up[k]]+=siz[dfn[k]];
}
void calc(int k,int from)
{
	modify(dfn[k],dfn[k]+siz[dfn[k]]-1,n-siz[dfn[k]]+sum[dfn[k]]);
	if(up[k]) modify(dfn[k],dfn[k]+siz[dfn[k]]-1,siz[up[k]]-n-sum[up[k]]);
	else next[dfn[k]]=las[c[k]],las[c[k]]=dfn[k];
	for(int i=fir[k];i;i=nex[i])
		if(to[i]!=from) calc(to[i],k);
}
int main()
{
	freopen("mushroom.in","r",stdin);
	freopen("mushroom.out","w",stdout);
	int i,j,x,y;ll v;
	read(n);
	for(i=1;i<=n;++i) read(c[i]);
	for(i=1;i<n;++i) read(x),read(y),inc(x,y);
	dfs(1,0),calc(1,0);
	for(i=0;i<=n;++i)
	{
		for(j=las[i],v=0;j;j=next[j]) v+=siz[j];
		modify(1,n,v);
		for(j=las[i];j;j=next[j]) modify(j,j+siz[j]-1,-v);
	}
	for(i=1;i<=n;++i) ans[i]=ans[i-1]+tag[i];
	for(i=1;i<=n;++i) printf("%lld\n",ans[dfn[i]]+n);
	return 0;
}