关于奈奎斯特采样中的频率镜像
在学习数字信号处理时,经常提到奈奎斯特采样定律,也经常看到下图:
很多时候,对上图横坐标fs处的虚线频谱不理解,怎么就有那个虚线了呢?那个虚线处,一般说是镜像频谱。
现在举例说明:
假如有两个sine波形,一个频率是1000Hz,另外一个频率是7000Hz.
s0 = sin(2*pi*1000*t), pi表示圆周率3.1415926......
s1 = sin(2*pi*7000*t)
我们知道,这两个sine波是不一样的,一个是1000Hz频率,一个是7000Hz频率,如果播放出来,给人的听觉是完全不同的。
上面两个波形是用连续信号(或者说模拟信号)的方式表达的。现在,我们要对他们进行数字化并存储下来,不幸的是,我们只有一个8000Hz采样率的采样设备,即一秒钟能采样8000个点。每个点我们用x[k]来表示,其中k是0,1,2,3,4.....的整数。那么,每个点的采样时间间隔就是 1/8000秒。
所以,每个点的采样时间点在:
0秒 1/8000秒 2/8000秒 .......... k/8000秒.........
则对s0采样,可以表示为:
x0[k] = sin( 2*pi*1000*(1/8000*k) )
对s1采样,可以表示为:
x1[k] = sin(2*pi*7000*(1/8000*k) )进一步整理得到
x1[k] = sin(2*pi*(8000 - 1000)*(1/8000*k) )
= sin(2*pi*8000*(1/8000*k) - 2*pi*1000*(1/8000)*k)
= sin(2*pi*k - 2*pi*1000*(1/8000*k) )
= - sin(2*pi*1000*(1/8000*k))
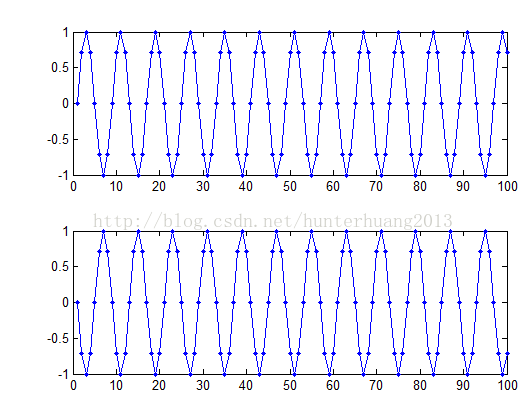
可以看到x0[k] 与 x1[k]序列,只是符号相反,幅度是完全相同的。也就是说,频率相同,相位相反。
更一般的,假设一个频率是f0(令其小于fs/2),另外一个频率是fs - f0,其中fs是采样频率。
则
x[k] = sin(2*pi*(fs-f0) * 1/fs * k )
= sin(2*pi*k - 2*pi*f0*1/fs*k)
= -sin(2*pi*f0*1/fs*k)
所以,fs - f0频率的sine波,与f0频率的sine波,在用fs采样率来采样的话,会得到频率相同相位相反的序列。
matlab代码如下:
fs=8000;
t=[0:1/fs:1];
f0 = 1000;
f0_mirror = 7000;
x = sin(2*pi*f0*t);
x_mirror = sin(2*pi*f0_mirror*t);
subplot(2,1,1),plot(x(1:100),'.-');
subplot(2,1,2),plot(x_mirror(1:100),'.-');
得到如下图形: