蓝桥杯学习之数据结构——图论基础知识简介
##1.图的基本概念:
图是由一系列顶点和若干连结顶点集合内两个顶点的边组成的数据结构。
数学意义上的图,指的是由一系列点与边构成的集合,这里我们只考虑有限集。通常我们用G = (V, E)表示一个图的结构,其中V表示点集, E表示边集。
在顶点集合所包含的若干个顶点之间,可能存在着某种两两关系——如果某两个点之间的确存在这样的关系的话,我们就在这两个点之间连边,这样就得到了边集的一个成员,也就是一条边,对应到社交网络中,顶点就是网络中的用户,边就是 用户之间的好友关系。
在图中也分有向边和无向边。
有向边:一条有向边必然是从一个点指向另一个点,并且相反方向的边一定不存在,如图:

无向边:有的时候我们不在意构成一条边的两个顶点谁先谁后,那么可以称为无向边。
由有向边组成的图为有向图,由无向边构成的则为无向图。
##2.形象化图:
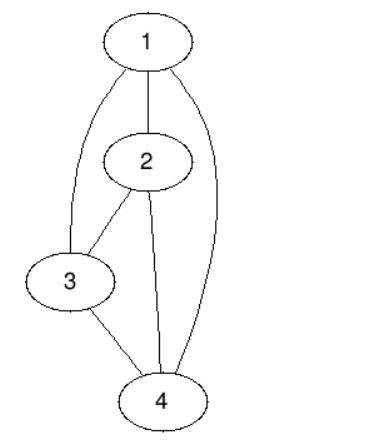
无向图:
用集合V表示点集合,集合E表示边集合
V(G) = {1, 2, 3, 5, 6}
E(G) = {(1,2), (2,3), (1,5), (2,6), (5,6)}
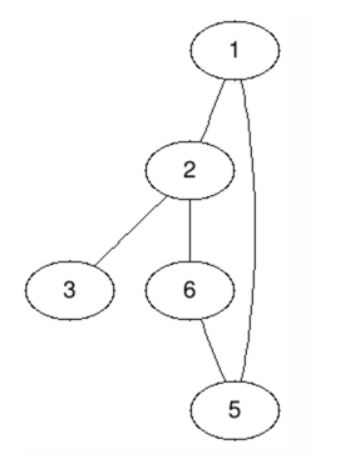
有向图:
在有向图中,连接边的顶点是有序的,箭头方向表示有向边的方向。
用集合V表示点集合,集合E表示边集合。
V(G’) = {1, 2, 3, 5, 6}
E(G’) = {(1,2), (2,3), (1,5), (2,6), (6,5)}
对于每一条边的(u,v)
我们称其为从u到v的一条有向边.
注:(u,v)和(v,u)是不同的两条边。
![]()
##4.图中的度:
a.无向图中的度:
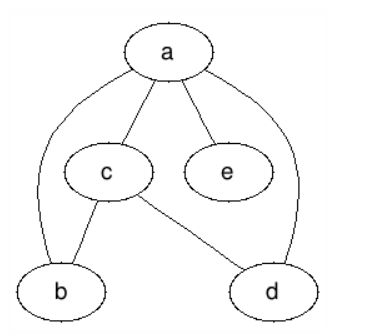
在无向图中,顶点的度是指某一个顶点连出的边数。例如下图:
顶点a的度是4,顶点b的度是3.
b。有向图的度:
在有向图中,和度对应的是入度和出度。顶点的入度是指以该顶点为终点的边的数量;顶点的出度是以顶点为起点的有向边数量。
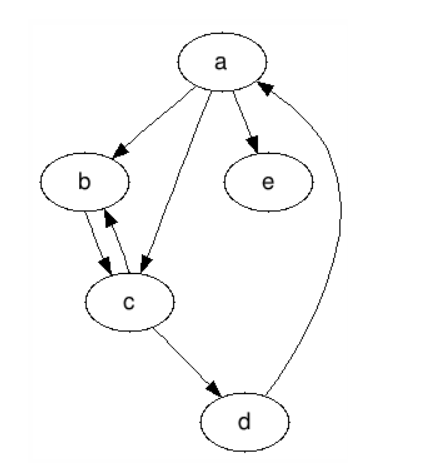
如下图:
顶点a的入度是1,出度是3,顶点b的入度是2, 出度是1。
##5.图在计算机内的存储——邻接矩阵:
a.邻接矩阵概念:
什么是邻接矩阵?所谓邻接矩阵存储结构就是每一个顶点用一个一维数组存储边的信息,这样所有点合起来就是用矩阵表示图中各个顶点之间的邻接关系。所谓矩阵其实就是一个二维数组。
对于n个顶点的图G=(V,E)来说,我们用一个n*n的矩阵A来表示G中的各顶点的相邻关系,如果vi和vj之间存在边或者弧,则a[i][j] = 1,否则a[i][j]=0,如图:
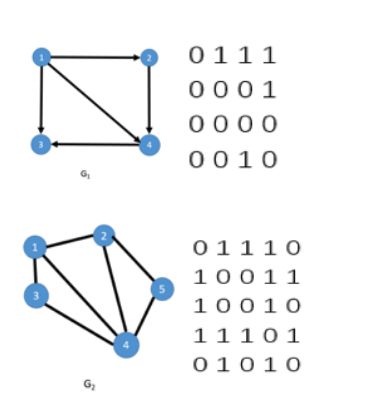
b.邻接矩阵的用途1:
一个邻接矩阵是唯一的,矩阵的大小只与顶点个数N有关,是一个N*N的矩阵。
用来求边的数量:
在无向图里,如果顶点vi和vj之间有边,则可认为vi到vj有边。对应到邻接矩阵中有a[i][j] = a[j][i] = 1;
用来计算有向图的出度与入度
顶点的出度即为邻接矩阵上点对应行上所有值的总和,比如下图中顶点1的出度为0 + 1 + 1 + 1 = 3;而每一个顶点的入度为每一列上所有值的和,如顶点3入度为1 + 0 + 0 + 1 = 2;
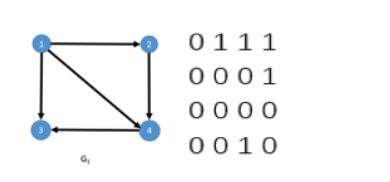
c.构建邻接矩阵:

例题:
众所周知,朋友之间关系并不是双向的,比如小明把小红当成朋友,但是小红不一定要把小明当成朋友,可能小红比较傲娇,所以我们需要用有向图来记录朋友之间的关系。班上一共5名同学,同学的编号为1 - 5.
而如果是朋友的话,必须要你把他当做朋友,且他也将你当成朋友,这个题目就是构建一个邻接矩阵存储有向图,在找有没有互相当做朋友,邻接矩阵的G[i][j] = 1表示i号把j号当成朋友,所以有如下条件即为真正的朋友:
G[i][j] == 1 && G[j][i] == 1
给出完整代码:
#include 运行截图:
![]()
##6.图的存储——邻接表:
a.邻接表简介:
邻接表的思想是,对于图中的每一个顶点,用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加,所以对于每一个点,我们需要用Vector来记录。
也就是对于每一个点,我们都用一个vector来记录这个点和哪些点相连。比如对于一张有10个点的图vector G[11]就可以用来记录这张图了。对于一条从a到b的有向边,我们通过G[a].push_back(b)就可以把这条边添加进去;如果是无向边,则需要在G[a].push_back(b)的同时G[b].push_back(a)即可。
如下图:
注:每一行的第一列表示的是最外层vector数组的下标。
![]()
b.邻接表与邻接矩阵的比较:

当然邻接矩阵比邻接表好的地方就在于随机查询。
比如,我们需要询问点a是否和b相连,我们就要遍历G[a],检查这个vector中是否有b。而在邻接矩阵中,只需要根据G[a][b]即能判断。
因此,我们需要对不同的应用情景选择不同的存图方法。如果是稀疏图(顶点多、边很少),一般用邻接表;如果是稠密度(顶点很少,边很多),一般用邻接矩阵。
c.邻接表code实现:
#include ##7.带权值的图:
a.带权图简介:
之前介绍的都是用图中的边表示两个点之间是否存在关系,而没有体现出两个点之间关系的强弱。比如在社交网络中,不能单纯地用0、1来表示两个人是否为朋友。当两个人是朋友时,有可能是很好的朋友,也有可能是一般的朋友,还有可能是不熟悉的朋友。
我们用一个数值来表示两个人之间的朋友的关系强弱,两个人的朋友关系越强,对应的值就越大。而这个值就是两个人在图中对应的边的权值,简称:边权。对应的图我们称之为带权图。
如下是一个带权图,我们把每条边对应的边权标记在边上:
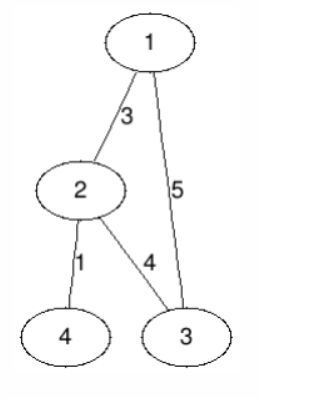
b.带权图的存储
依然是两种存储方式:
1.邻接矩阵:
用G[a][b]来表示a和b之间的边权(我们需要用一个数值来表示边不存在,如0)。同样,对于无向图,这个矩阵依然是对称的。
对于上面的带权图,
我们可以用邻接矩阵做如下存储。
0 3 5 0
3 0 4 1
5 4 0 0
0 1 0 0
2.邻接表:
用邻接表存储略微不同,我们需要用一个结构体来记录一条边连接的点和这条边的边权,然后用一个vector来存储若干结构体
struct node {
int v; // 用来记录连接的点
int len; // 用来记录这条边的边权
};
我们通常把向图中加入一条边写成一个函数,例如加入一条有向边(u,v)、边权为w,就可以用如下的函数来实现(我们需要把图定义成全局变量)
vector<node> G[110];
// 插入有向边
void insert1(int u, int v, int w) {
node temp;
temp.v = v;
temp.len = w;
G[u].push_back(temp);
}
而插入无向边的话,实际上相当于插入两条方向相反的有向边:
// 插入无向边
void insert2(int u, int v, int w) {
insert1(u, v, w);
insert1(v, u, w);
}
c.带权图邻接表实现code:
#include ##8.邻接表的链表使用:
a.简介:
在实现邻接表时,我们使用了vector这个结构来存储从每个顶点连出的所有边。但是,由于vector常数较大,对于某些时间限制较为严格的场景,使用vector极有可能吃T。
因此,我么用更高效的存储从一个顶点连出的所有边的方法——基于链表的邻接表。
const int M = 1000000;
const int N = 10000;
struct edge {
int v, d, next;
} e[M];
int p[N], eid;
void init() { // 初始化,在建图之前必须进行
memset(p, -1, sizeof(p));
eid = 0;
}
void insert(int u, int v, int d) { // 插入单向边
e[eid].v = v;
e[eid].d = d;
e[eid].next = p[u];
p[u] = eid++;
}
void insert2(int u, int v, int d) { // 插入双向边
insert(u, v, d);
insert(v, u, d);
}
void output(int n) { // 输出整张图中的所有边
for (int i = 0; i < n; i++) {
for (int j = p[i]; j != -1; j = e[j].next) { // 遍历从 i 连出的所有边
cout << i << "->" << e[j].v << ", " << e[j].d << endl;
}
}
}
欢迎关注
ly’s blog