MXnet代码实战之正则化
关于正则化的一些思考
机器学习的很多算法都是用多项式函数去逼近的。但是大家有没有产生疑问,为什么可以这样?这个时候只要我们想起伟大的泰勒公式,我想大家面对这个疑问心里就会舒坦很多,还记得我们在大学的时候学习高等数学当中的泰勒展开式,任何函数比如log x,lnx,1/x等等都可以用多项式去趋近。而不同的函数曲线其实就是这些基础函数的组合,自然也可以用多项式去趋近。
好,但是当多项式的项数太多的时候,函数就会过拟合,过拟合的意思就是模型在训练集上表现的很好,但是在测试集上表现的很差。这个时候,正则就派上用场了。正则就是用来惩罚函数的,不能让你学的太好,不能让你针对训练数据集拟合的太好。这个地方,我曾经迷糊了一阵,很多书上仅仅只是提到正则能够做到这一点,但是没有解释它为什么能做到这一点,正好最近有点感触,先简单说一些。对于多项式函数,过拟合的原因是项数太多,那我们可以定义一个函数加在多项式函数后面,用来保证最小化多项式函数项数,其实就是让W向量中项的个数最小化。求W向量中项的个数最小化其实就是0范数(0范数,向量中非零元素的个数)。意思就是说要让W向量中非0元素最少(为0的项最多),那就是在要求模型在保证训练误差最小化的同时保证项数最少。后面又有人把其推广到L1和L2范数(有人证明过)。
从0实现正则化例子
代码:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
#Author: yuquanle
#2017/10/11
#沐神教程实战之正则化学习
#本例子使用人工生成数据集
from mxnet import ndarray as nd
from mxnet import autograd
from mxnet import gluon
num_train = 20
num_test = 100
num_inputs = 200
# 生成数据集
# 定义模型真实的参数
true_w = nd.ones((num_inputs, 1)) * 0.01
true_b = 0.05
# ⽣成训练和测试数据集
X = nd.random.normal(shape=(num_train + num_test, num_inputs))
Y = nd.dot(X, true_w)
Y += .01 * nd.random.normal(shape=Y.shape)
X_train, X_test = X[:num_train], X[num_train:]
Y_train, Y_test = Y[:num_train], Y[num_train:]
# 定义⼀个函数它每次返回batch_size 个随机的样本和对应的⽬标
import random
batch_size = 1
def data_iter(num_examples):
idx = list(range(num_examples))
random.shuffle(idx)
for i in range(0, num_examples, batch_size):
j = nd.array(idx[i:min(i + batch_size, num_examples)])
yield X.take(j), Y.take(j)
# 初始化模型参数
def get_params():
w = nd.random.normal(shape=(num_inputs, 1)) * 0.1
b = nd.zeros((1,))
for param in (w, b):
param.attach_grad()
return (w, b)
# L2 范数正则化
def L2_penalty(w, b):
return (w ** 2).sum() + b ** 2
# 定义训练和测试
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 120
import matplotlib.pyplot as plt
def net(X, lambd, w, b):
return nd.dot(X, w) + b
def square_loss(yhat, y):
return (yhat - y.reshape(yhat.shape)) ** 2
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
def test(params, X, y):
return square_loss(net(X, 0, *params), y).mean().asscalar()
def train(lambd):
epochs = 10
learning_rate = 0.002
params = get_params()
train_loss = []
test_loss = []
for e in range(epochs):
for data, label in data_iter(num_train):
with autograd.record():
output = net(data, lambd, *params)
# 加入L2正则,惩罚过于复杂的模型
loss = square_loss(output, label) + lambd * L2_penalty(*params)
loss.backward()
SGD(params, learning_rate)
train_loss.append(test(params, X_train, Y_train))
test_loss.append(test(params, X_test, Y_test))
plt.plot(train_loss)
plt.plot(test_loss)
plt.legend(['train', 'test'])
plt.show()
return 'learned w[:10]:', params[0][:10], 'learend b:', params[1]
# 测试
# 先不用正则化,lamda=0
train(0)
# 使用lamda=2的正则化
# train(2.5)
结果分析:
当不用正则时,训练误差下来了,但是测试误差还是很大。如图:
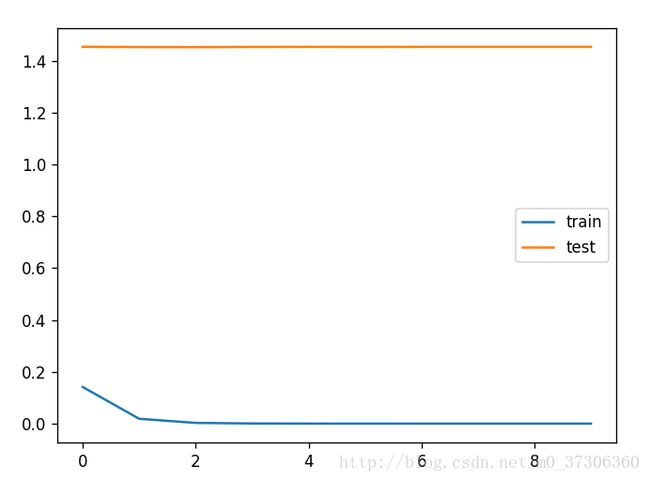
当使用正则时,lambad取2.5,训练集误差和测试集误差趋向一致,结果如下图:

使用Gloun
代码:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
#Author: yuquanle
#2017/10/11
#沐神教程实战之正则化学习
#本例子使用人工生成数据集
#使用gluon
from mxnet import ndarray as nd
from mxnet import autograd
from mxnet import gluon
num_train = 20
num_test = 100
num_inputs = 200
true_w = nd.ones((num_inputs, 1)) * 0.01
true_b = 0.05
X = nd.random.normal(shape=(num_train + num_test, num_inputs))
y = nd.dot(X, true_w)
y += .01 * nd.random.normal(shape=y.shape)
X_train, X_test = X[:num_train, :], X[num_train:, :]
y_train, y_test = y[:num_train], y[num_train:]
import matplotlib.pyplot as plt
import matplotlib as mpl
batch_size = 1
dataset_train = gluon.data.ArrayDataset(X_train, y_train)
data_iter_train = gluon.data.DataLoader(dataset_train, batch_size, shuffle=True)
square_loss = gluon.loss.L2Loss()
def test(net, X, y):
return square_loss(net(X), y).mean().asscalar()
def train(weight_decay):
learning_rate = 0.005
epochs = 10
net = gluon.nn.Sequential()
with net.name_scope():
net.add(gluon.nn.Dense(1))
net.initialize()
# 注意到这⾥ 'wd':weight decay
# 通过优化算法的wd参数实现对模型的正则化(相当于 L2 范数正则化)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
'learning_rate': learning_rate, 'wd': weight_decay})
train_loss = []
test_loss = []
for e in range(epochs):
for data, label in data_iter_train:
with autograd.record():
output = net(data)
loss = square_loss(output, label)
loss.backward()
trainer.step(batch_size)
train_loss.append(test(net, X_train, y_train))
test_loss.append(test(net, X_test, y_test))
plt.plot(train_loss)
plt.plot(test_loss)
plt.legend(['train', 'test'])
plt.show()
return ('learned w[:10]:', net[0].weight.data()[:, :10],
'learned b:', net[0].bias.data())
train(6)