【欧拉回路】讲解+判定+输出“点”路径
首先来系统地整理一下有关欧拉回路和欧拉路径的问题。
什么是欧拉路径?在图上用一种走法经过所有的边一次且只有一次的路径叫做欧拉路径。即一笔画。
如果这条路径的起点和终点重合,那么就是欧拉回路。
如何判断图是否有欧拉回路或者欧拉路径?
无向图:因为欧拉路径中,除了起点与终点以外,任意点的“进”“出”次数相等,所以除了两个点为奇点(度数为奇数的点)(终点和起点)以外,其它点的度数均为偶数。
如果是欧拉回路,奇点的个数应该为0。
有向图:欧拉路径中,最多只有两个点的入度不等于出度。起点出度比入度大1,终点入度比出度大1。
如果是欧拉回路,所有点的 入度=出度 。
寻找欧拉回路或欧拉路径的算法有?
Fluery算法和Hierholzers算法。后者好像也有博客称逐步插入回路法。
后面一种算法无论是编程复杂度还是时间复杂度好像都比前种算法复杂度更优,但前者的应用广泛性好像比后者更高。欧拉回路的更高级的应用还没涉及,如果之后有什么新内容再来补充吧....所以这里就用Hierholzers算法了。
Hierholzers算法自动寻找欧拉回路,在找不到欧拉回路的情况下会找到欧拉路径。前提是得给它指定好起点。
算法流程(无向图):
1.判断奇点数。奇点数若为0则任意指定起点,奇点数若为2则指定起点为奇点。
2.开始递归函数Hierholzers(x):
循环寻找与x相连的边(x,u):
删除(x,u)
删除(u,x)
Hierholzers(u); //递归!
将x插入答案队列之中
3.倒序输出答案队列
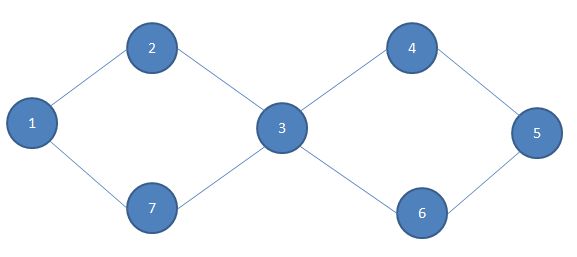
对于该图,算法的执行流程如下:
1.找到该图没有奇点,从1开始进行Hierholzers算法。
2.删边1-2 递归到2
3.删边2-3 递归到3
4.删边3-7 递归到7
5.删边7-1 递归到1
6.1无边,1加入队列,返回
7.7加入队列,返回
8.删边3-4 递归到4
9.删边4-5 递归到5
10.删边5-6 递归到6
11.删边6-3 递归到3
12.3加入队列,返回
13.6加入队列,返回
14.5加入队列,返回
15.4加入队列,返回
16.3加入队列,返回
17.2加入队列,返回
18.1加入队列,返回
答案队列为:1 7 3 6 5 4 3 2 1。反向输出即为答案。
有向图除判断是否存在有一点点不同以外同理。
【欧拉回路的判定】
大致思路:
这个代码可以当模板用。
就是跟上面讲的算法流程一样的思路,判定这个无向图有没有欧拉回路首先就是看它有没有度为奇数的点,若有的话欧拉回路一定不成立。但这个不是必要条件,满足了之后还需要去找欧拉回路,如果能经历所有边,那么就说明有欧拉回路!
#include
#include
using namespace std;
const int MAXN=1010;
vector v[MAXN];
int N,M;
int cnt=0;
void olahuilu(int s)
{
for(auto t=v[s].begin();t!=v[s].end();t=v[s].begin())
{
int a=*t;
v[s].erase(t);
v[a].erase(find(v[a].begin(),v[a].end(),s));
cnt++;
olahuilu(a);
}
//road[count++]=s;
}
int main()
{
cin>>N>>M;
int temp=M;
while(M--)
{
int a,b;
cin>>a>>b;
v[a].push_back(b);
v[b].push_back(a);
}
for(int i=1;i<=N;i++)
{
if(v[i].size()%2!=0)
{
cout<<0;
return 0;
}
}
olahuilu(1); //因为无向图找欧拉回路,所以从任意一个起点开始即可
if(temp==cnt) cout<<1;
else cout<<0;
return 0;
} 代码中学到的点:
首先是除了用链式前向星存储,这里还用到容器vector来“建图”,由于是无向图所以要双向建边,从而,olahuilu函数里“消边”也要双向地消!
所以比较有收获的olahuilu那个函数里面,首先是auto指针类型,然后了解到vector的erase()用法是:
所以参数是个指针!然后 find(vec.begin(),vec.end(),x) 正是返回vec容器里值为x的那个元素的指针!所以我们从该边的另一个端点的容器里这样erase掉对应的点,达到双向地消除边的目的!
注意要递归,别漏写了。
另外关于vector的erase方法,还可多了解:
PS:本题中的使用方法是 it=v[s].begin(),因为删了这个边嘛,继续指向第一个就是指向下一个边了,反正就是不能用it++,避免使用“野指针”。
【输出欧拉路径/回路的“点”路径】
对于该题【欧拉路径/欧拉回路】模板题,要求输出答案的最小序列。所以起点首先要选的尽量小,然后在边的储存上面加一点小trick。
使用邻接表储存图时,除了用链式前向星还可以用vector储存。我们可以把vector换成multiset,这样就可以保证该点前往的下一个点是最小值,同时保证了答案的最小值。
#include
using namespace std;
const int N=1025;
multiset to[N];
int len[N];
int road[N],k;
void dfs(int x){
for(auto a=to[x].begin();a!=to[x].end();a=to[x].begin()){//auto类型为C++11标准,可进行自动类型推断
int u=*a;
to[x].erase(a);
to[u].erase(to[u].find(x));//删边
dfs(u);//递归
}
road[k++]=x;//往答案队列里插入答案
}
int main(){
int m,a,b;
scanf("%d",&m);
for(int i=0;i=0;k--)
printf("%d\n",road[k]);//倒序输出答案 注意是倒序 因为涉及了递归,先走到的点等后面的点递归完了才加入数组
return 0;
} 学到的点:
set都懂,而multiset和set的唯一区别在于multiset可以有重复元素!!!