CCF-201312-4（有趣的数）

一：问题
1.问题描述

我们把一个数称为有趣的，当且仅当：
　　1. 它的数字只包含0, 1, 2, 3，且这四个数字都出现过至少一次。
　　2. 所有的0都出现在所有的1之前，而所有的2都出现在所有的3之前。
　　3. 最高位数字不为0。
　　因此，符合我们定义的最小的有趣的数是2013。除此以外，4位的有趣的数还有两个：2031和2301。
　　请计算恰好有n位的有趣的数的个数。由于答案可能非常大，只需要输出答案除以1000000007的余数。

2.格式

输入格式
　　输入只有一行，包括恰好一个正整数n (4 ≤ n ≤ 1000)。
输出格式
　　输出只有一行，包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。

3.样例

样例输入
4
样例输出
3

二：理解
题意：就是先确定一个数的位数，然后按着要求找满足要求的数的个数。
要求：
1.必须含有0,1,2,3且只含有这四个数
2.所有的0都出现在所有的1之前，而所有的2都出现在所有的3之前

理解：

1.在满足题意的情况下，首位只能是2，因为最高位不为0，如果最高位为1，则不满足0在1之前，最高位为3则不满足2在3之前，所以最高位只能为2.

2.采用动态规划思想，每一次决策都基于前一次决策的最优解。即对一个n位数的解都基于前一个n－1位的数的最优解。

解法：
1.我们对一个数的第n位规定一个状态集：即到这一位为止还有几个数字没有使用（假设我们有0123共四个数）。

注：我们只需要将每个数填入即可，而不是看数的个数
就是 203和230是一个状态集；

根据规则来说，共有6种状态：
0－－用了2，剩0，1，3
1－－用了2，0，剩1，3
2－－用了2，3，剩0，1
3－－用了2，0，1，剩3
4－－用了2，0，3，剩1
5－－全部用了

于是我们需要让用户输入位数，然后声明同等位数的数组，在每个元素里是6种状态中所包含的该状态下的“符合条件的数”的个数。
2.位数大于4之后就会有重复的情况发生，怎么处理这个情况呢？

上面这些就是在对应状态下，发生重复的情况。

3.第i位出现第j种状态的情况数表示为 status[i][j]
i位数的来源在于（i-1）位数（已经按顺序排列）+最后一位数字

例如：
status[i][0] = status[i-1][0] ;
使用过2 的情况可以由： 前i-1位使用2（状态0），第i位使用2。

status[i][1] = (status[i-1][0] + status[i-1][1] *2);
使用过 2 0 的情况可以由：
前i-1位使用2（状态0）
第i位使用0前i-1位使用2 0（状态1）
第i位使用0或2 （顺序正确）。

status[i][2] = (status[i-1][0] + status[i-1][2] );
使用过 2 3 的情况可以由：
前i-1位使用2（状态0），第i位使用3
前i-1位使用2 3（状态2），第i位使用3 （因为已经有了3了不能用2了，只能用3）

status[i][3] = (status[i-1][1] + status[i-1][3] *2);
使用过 2 0 1 的情况可以由：
前i-1位使用2 0（状态1），第i位使用1
前i-1位使用2 0 1（状态3），第i位使用1或2　（因为已经有了1了不能用0了，只能用1）

status[i][4] = (status[i-1][1] + status[i-1][2] + status[i-1][4] *2);
使用过 2 0 3 的情况可以由：
前i-1位使用2 0（状态1），第i位使用3
前i-1位使用2 3（状态2），第i位使用0
前i-1位使用2 0 3（状态4），第i位使用0或3 （因为已经有了3了不能用2了，只能用3）
　　　　　　
a[i][5] = (a[i-1][3] + a[i-1][4] + a[i-1][5] *2);
使用过2 3 0 1的情况可以由：
前i-1位使用2 0 1（状态3），第i位使用3
前i-1位使用2 0 3（状态4），第i位使用1
前i-1位使用2 3 0 1（状态5），第i位使用1或3
（因为已经有了1了不能用0了，只能用1）
（因为已经有了3了不能用2了，只能用3）

4.重点代码：
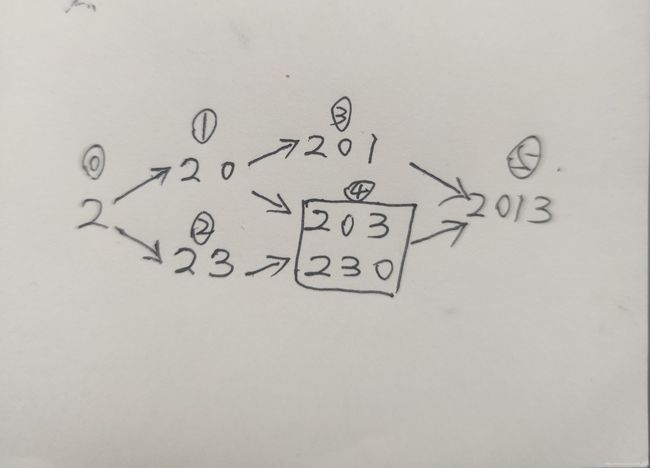
这个看着状态图更容易：

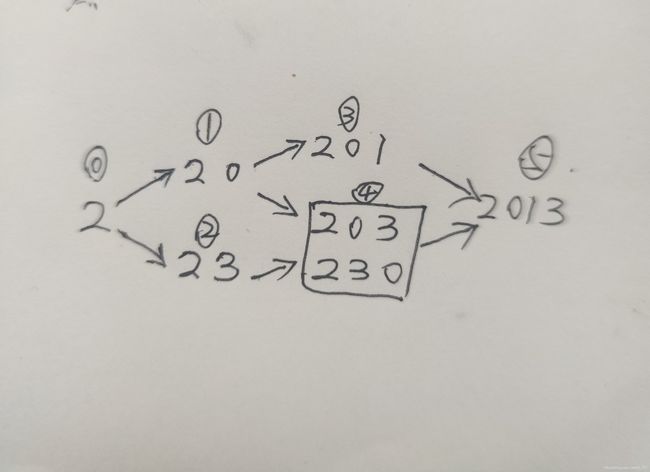
求一个状态就是看有几个重复的状态，有几个状态指向他。
例：
status[i][2] = (status[i - 1][2] + status[i - 1][0]) % mod;
就是他只有一个重复的状态，且状态0指向他。
同时
status[i][3] = (status[i - 1][3] * 2 + status[i - 1][1]) % mod;
有两个重复的状态，且状态1指向他。
全部思路代码：

status[i][0] = 1;
status[i][1] = (status[i - 1][1] * 2 + status[i - 1][0]) % mod;
status[i][2] = (status[i - 1][2] + status[i - 1][0]) % mod;
status[i][3] = (status[i - 1][3] * 2 + status[i - 1][1]) % mod;
status[i][4] = (status[i - 1][4] * 2 + status[i - 1][2] + status[i - 1][1]) % mod;
status[i][5] = (status[i - 1][5] * 2 + status[i - 1][4] + status[i - 1][3]) % mod;

注：答案可能非常大，会爆int，应该用long 。
由于答案可能非常大，只需要输出答案除以1000000007的余数。

三：代码
参考：
https://www.cnblogs.com/haimishasha/p/5323394.html
https://blog.csdn.net/u013580497/article/details/48326879
https://www.cnblogs.com/Outer-Haven/p/4688752.html

#include
#include
using namespace std;

int main()
{
	long mod = 1000000007;
	long long status[1005][6];
	int n;
	cin >> n;
	for(int j=0; j<6; j++)
		status[0][j] = 0;
	for(int i=1; i<=n; i++)
	{
		int j = i - 1;
		status[i][0] = 1;
		status[i][1] = (status[j][1]*2 + status[j][0]) % mod;
		status[i][2] = (status[j][2] + status[j][0]) % mod;
		status[i][3] = (status[j][3]*2 + status[j][1]) % mod;
		status[i][4] = (status[j][4]*2 + status[j][1] + status[j][2]) % mod;
		status[i][5] = (status[j][5]*2 + status[j][3] + status[j][4]) % mod;
	}
	cout << status[n][5] << endl;
	return 0;
}