跳跃游戏系列题目【动态规划&贪心算法&DFS&BFS】

Leetcode 55. 跳跃游戏

问题描述

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。${}^{[1]}$

解题报告

有两种方法

动态规划

$dp[i]$ 表示 第 i 个位置是否可达。
转移方程为：
$$dp[i]=\{\begin{array}{c}0ifnums[0:i-1]中能找到dp[j]使得dp[j]+j>=i且第j个位置可达;\\ 1otherwise;\end{array}$$
时间复杂度 $O(N^2)$

贪心算法

持续更新变量 MAXX，其表示当前能跳的最远位置。
当遍历到某个位置 i 时，如果 i>MAXX，则表示从 i 这个地方断掉了，所以无法跳到最后位置，直接返回 false 即可。

实现代码

动态规划实现

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n=nums.size();
        if(n==1){
            return 1;
        }
        vector<int>dp(n,0);
        dp[0]=1;
        for(int i=0;i<n;i++){
            for(int j=i-1;j>=0;j--){
                if(dp[j]&&j+nums[j]>=i){
                    dp[i]=1;
                    break;
                }
            }
        }
    return dp[n-1];
    }
};

贪心算法实现

class Solution {
public:
    bool canJump(vector<int>&nums){
        int MAXX=0;
        for(int i=0;i<nums.size()&&MAXX<nums.size();i++){
            if(i>MAXX) return false;
            MAXX=max(MAXX,i+nums[i]);
        }
        return true;
    }
};

Leetcode 45. 跳跃游戏 II

问题描述

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:

假设你总是可以到达数组的最后一个位置。${}^{[2]}$

解题报告

动态规划

见代码注释。

贪心算法

维持一个变量 MAXX 来记录当前位置所能跳的最远距离，并不是每一次更新最远跳跃距离实际上是要跳的。例如在位置 0，我们能到达的最远距离是 0+nums[0]，但是在到达 0+nums[0] 前我们会多次更新最远跳，而我们不知道哪个位置是实现最少跳跃的局部位置。${}^{[3]}$

\qquad实际上，我们只需要知道一点：在到达位置 0+nums[0] 后，我们必然需要再跳一次，这样我们才能继续前进。 所以我们另外维持一个变量 pos，它记录的是在我们在执行跳跃动作时能到达的最远位置，即为当前时刻的 MAXX。每当我们到达边界时，跳跃步数加 1 ，更新边界。${}^{[4]}$

实现代码

动态规划实现

#include
#define maxn 105
int dp[maxn];
int aa[maxn];
///dp[i]中i表示从第0号位置达到i号位置所需要的最小跳跃数
void dg(int a[],int n)
{
    dp[0]=0;///终点是0号位置时，不需要跳跃
    for(int i=1; i<n; i++)
    {
        for(int j=0; j<i; j++)
        {
///j从小变到大，当发现从j号位置能跳到i号位置时，判断dp[j]+1是否小于dp[i]，从而决定是否更新dp[i]的值
            if(aa[j]+j>=i)
            {
                if(dp[j]+1<dp[i])
                {
                    dp[i]=dp[j]+1;
                }
            }
        }
    }
}
int main()
{
    int n;
    for(int i=0; i<maxn; i++)
        dp[i]=99999999;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=0; i<n; i++)
            scanf("%d",&aa[i]);

        dg(aa,n);
        printf("%d\n",dp[n-1]);
    }
    return 0;
}

贪心算法实现

class Solution {
public:
    int jump(vector<int>&nums){
        int ans=0, pos=0, MAXX=0;
        for(int i=0;i<nums.size()-1;i++){
            MAXX=max(MAXX, i+nums[i]);
            if(i==pos){
                pos=MAXX;
                ans++;
            }
        }
        return ans;
    }
};

Leetcode 1306. 跳跃游戏 III

问题描述

这里有一个非负整数数组 arr，你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时，你可以跳到 i + arr[i] 或者 i - arr[i]。

请你判断自己是否能够跳到对应元素值为 0 的 任意 下标处。

注意，不管是什么情况下，你都无法跳到数组之外。

示例 1：

输入：arr = [4,2,3,0,3,1,2], start = 5
输出：true
解释： 到达值为 0 的下标 3 有以下可能方案： 下标 5 -> 下标 4 -> 下标 1 -> 下标 3 下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3

${}^{[5]}$

解题报告

DFS判断是否可达。从某个位置出发，判断是否能到达目标点。每个位置的出发的方向有两个，由此可建一棵规模一定的搜索树，使用深度优先搜索即可。

实现代码

class Solution {
public:
    bool dfs(vector<bool> visited,int idx){
        if(idx<0||idx>=temp.size()) return false;
        if(temp[idx]==0) return true;
        if (visited[idx]) return false;
        visited[idx]=true;
        return dfs(visited,idx+temp[idx])||dfs(visited,idx-temp[idx]);
    }
    bool canReach(vector<int>& _arr, int start) {
        temp = _arr;
        int size = temp.size();
        vector<bool> visited(size,false);
        return dfs(visited,start);
    }
private:
    vector<int> temp;
};

Leetcode 1345. 跳跃游戏 IV

问题描述

给你一个整数数组 arr ，你一开始在数组的第一个元素处（下标为 0）。

每一步，你可以从下标 i 跳到下标：

i + 1 满足：i + 1 < arr.length
i - 1 满足：i - 1 >= 0
j 满足：arr[i] == arr[j] 且 i != j
请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。

注意：任何时候你都不能跳到数组外面。

示例 1：

输入：arr = [100,-23,-23,404,100,23,23,23,3,404]
输出：3
解释：那你需要跳跃 3 次，下标依次为 0 --> 4 --> 3 --> 9 。下标 9 为数组的最后一个元素的下标。

${}^{[6]}$

解题报告

BFS求最短距离。
需要注意的是：

 if (m.find(arr[u]) != m.end()) {
   for (int v: m[arr[u]]) {
        if (!vis[v]) {
            vis[v] = 1;
            dis[v] = min(dis[u]+1, dis[v]);
            q.push(v);
        }
    }
    m.erase(arr[u]); // 访问过的值直接清理掉
}

在更新完某一元素 arr[i]时，当又遇到元素 arr[i] 时，我们不需要重新更新了。所以需要区分某重复元素【值相同，但是索引不同，所以 vis[] 无法限制】是否已经被更新。${}^{[7]}$

实现代码

class Solution {
public:
    int minJumps(vector<int>& arr) {
        int n = arr.size();
      
        vector<int> dis(n, INT_MAX); // 距离
        vector<int> vis(n, 0); // 访问标记
        unordered_map<int, vector<int>> m; // 倒排加速(m既起到了倒排加速作用，又起到了记录值是否被访问的作用，如果有一个值被访问过了，删除该值对应的键)
        for (int i = 0; i < n-1; i++) 
            m[arr[i]].push_back(i);
      
        dis[n-1] = 0; // 最后一个点入队
        vis[n-1]=1;
        queue<int> q;
        q.push(n-1);
      
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            if (u-1 >= 0 && !vis[u-1]) { // 左跳
                dis[u-1] = min(dis[u-1], dis[u]+1);
                vis[u-1] = 1;
                q.push(u-1);
            }
            if (u+1 < n && !vis[u+1]) { // 右跳
                dis[u+1] = min(dis[u+1], dis[u]+1);
                vis[u+1] = 1;
                q.push(u+1);
            }
            if (m.find(arr[u]) != m.end()) {
                for (int v: m[arr[u]]) {
                    if (!vis[v]) {
                        vis[v] = 1;
                        dis[v] = min(dis[u]+1, dis[v]);
                        q.push(v);
                    }
                }
                m.erase(arr[u]); // 访问过的值直接清理掉
            }
        }
        return dis[0];
    }
};

// 作者：inszva-2
// 链接：https://leetcode-cn.com/problems/jump-game-iv/solution/onti-jie-by-inszva-2/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Leetcode 1340. 跳跃游戏 V

问题描述

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

i + x ，其中 i + x < arr.length 且 0 < x <= d 。
i - x ，其中 i - x >= 0 且 0 < x <= d 。
除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

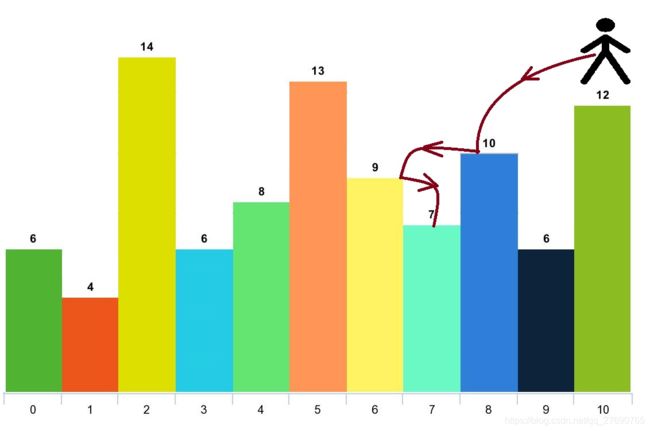
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

${}^{[8]}$

解题报告

对于任意的位置 i，根据第二个条件，我们只需要在其左右两侧最多扫描 d 个元素，就可以找出所有满足条件的位置 j。随后我们通过这些 j 的 dp 值对位置 i 进行状态转移，就可以得到 dp[i] 的值。

此时出现了一个需要解决的问题，如何保证在处理到位置 i 时，所有满足条件的位置 j 都已经被处理过了呢？换句话说，如何保证这些位置 j 对应的 dp[j] 都已经计算过了？如果我们用常规的动态规划方法（例如根据位置从小到大或者从大到小进行动态规划），那么并不能保证这一点，因为 j 分布在位置 i 的两侧。

因此我们需要借助记忆化搜索的方法，即当我们需要 dp[j] 的值时，如果我们之前已经计算过，就直接返回这个值（记忆）；如果我们之前没有计算过，就先将 dp[i] 搁在一边，转而去计算 dp[j]（搜索），当 dp[j] 计算完成后，再用其对 dp[i] 进行状态转移。

记忆化搜索一定能在有限的时间内停止吗？如果它不能在有限的时间内停止，说明在搜索的过程中出现了环。即当我们需要计算 dp[i] 时，我们发现某个 dp[j] 没有计算过，接着在计算 dp[j] 时，又发现某个 dp[k] 没有计算过，以此类推，直到某次搜索时发现当前位置的 dp 值需要 dp[i] 的值才能得到，这样就出现了环。在本题中，根据第三个条件，arr[j] 是一定小于 arr[i] 的，即我们的搜索每深入一层，就跳到了高度更小的位置。因此在搜索的过程中不会出现环。这样以来，我们通过记忆化搜索，就可以在与常规的动态规划相同的时间复杂度内得到所有的 dp 值。${}^{[9]}$

注意：深搜时，可以借助记忆化来解决 【如何保证在处理到位置 i 时，所有满足条件的位置 j 都已经被处理过了呢？】，当时用动态规划时，则需要提前对数组中元素进行从低到高排序。

实现代码

class Solution {
public:
	int maxJumps(vector<int>& arr, int d) {
		int n = arr.size();
		vector<vector<int>> temp;
		vector<int> dp(n, 0);
		int res = 1;
		for (int i = 0; i < arr.size(); i++)
			temp.push_back({ arr[i],i });
		sort(temp.begin(), temp.end());

		for (int i = 0; i < n; i++) {
			int index = temp[i][1]; //编号;
			dp[index] = 1;
			//向左找
			for (int j = index - 1; j >= index - d && j >= 0; j--) {
				if (arr[j] >= arr[index]) break;
				if (dp[j] != 0) dp[index] = max(dp[index], dp[j ] + 1);
			}
			//向右找
			for (int j = index + 1; j <= index + d && j < n; j++) {
				if (arr[j] >= arr[index]) break;
				if (dp[j] != 0) dp[index] = max(dp[index], dp[j] + 1);
			}
			res = max(dp[index], res);
		}
		return res;

	}
};
// 作者：wu-bin-cong
// 链接：https://leetcode-cn.com/problems/jump-game-v/solution/dp-dong-tai-gui-hua-fei-chang-hao-li-jie-by-wu-bin/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

${}^{[10]}$

参考资料

[1] Leetcode 55. 跳跃游戏
[2] Leetcode 45. 跳跃游戏 II
[3] 跳跃游戏二——动态规划
[4] Leetcode 45. 跳跃游戏 II【贪心算法O(n)时间复杂度，解释非常详细】
[5] Leetcode 1306. 跳跃游戏 III
[6] Leetcode 1345. 跳跃游戏 IV
[7] Leetcode 1345. 跳跃游戏 IV 题解区：inszva-2
[8] Leetcode 1340. 跳跃游戏 V
[9] Leetcode 1340. 跳跃游戏 V 官方题解
[10] Leetcode 1340. 跳跃游戏 V 题解区：wu-bin-cong