图论基础知识与常见图处理算法
本笔记涉及代码:https://github.com/hackeryang/Algorithms-Fourth-Edition-Exercises
1.图论应用广泛,例如地图中规划最短路线、搜索引擎中的网页链接(结点为网页)、电路板上元件之间的连接、商业交易中用连接表示现金和商品在买卖方之间的转移、编译器使用图表示大型软件系统中各模块之间的关系等(结点为模块,连接为类方法之间的调用关系),如下所示:
一、无向图
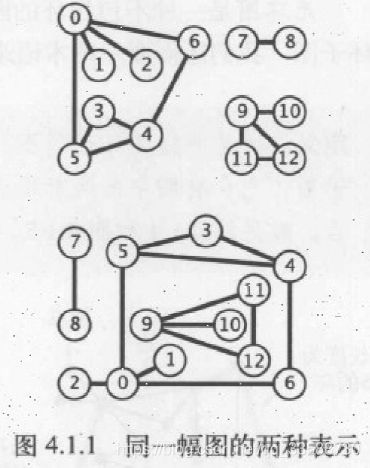
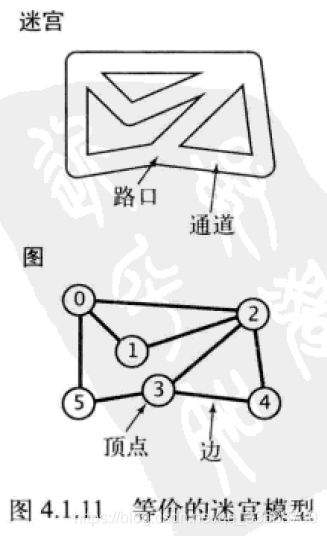
2.无向图指用一条没有方向(如箭头)的边(edge)连接两个顶点(vertex)的结构。对于无向图来说,两种图的形状可能实际上代表同一个图,因为结点之间的连接关系相同,如下所示:
如果一条边的两端都连接结点自身,称为自环,两个结点间都连接这两个结点的两条边称为平行边,含有平行边的图称为多重图,如下所示:
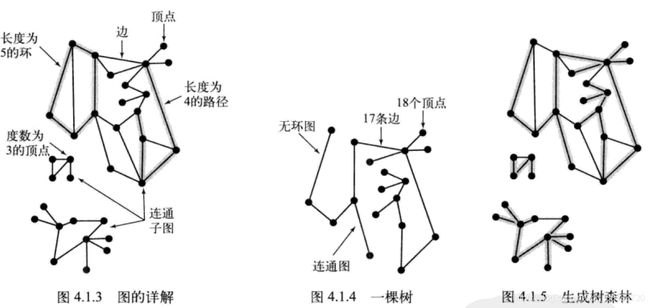
没有平行边或自环的图称为简单图。两个顶点通过一条边相连时,称这两个顶点相邻,并称这条边依附于这两个结点,某个顶点的度数即依附于它的边的总数。子图是由一幅图的所有边的一个子集及其所依附顶点组成的图。在一张图中,路径是由多条边顺序连接的一系列顶点,简单路径是一条没有重复顶点的路径,简单环是一条除起点和终点结点相同以外不含有其他重复顶点和边的环。
3.如果任意一个顶点都存在一条路径到达另一个任意顶点,称这幅图为连通图。一幅非连通的图由若干连通的部分组成,他们都是极大连通子图。无环图是一种不包含环的图,树是一幅无环连通图,互不相连的树组成的集合称为森林。连通图的生成树是该图的一幅子图,它含有图中的所有顶点且是一棵树,图的生成树森林是它所有连通子图的生成树的集合,如下所示:
当且仅当一幅含有V个结点的图G满足下列5个条件之一时,它就是一棵树:
(1)G有V-1条边且不含环;(2)G有V-1条边且是连通的;(3)G是连通的,但删除任意一条边都会使它不再连通;(4)G是无环图,但添加任意一条边都会产生一条环;(5)G中的任意一对顶点之间仅存在一条简单路径。
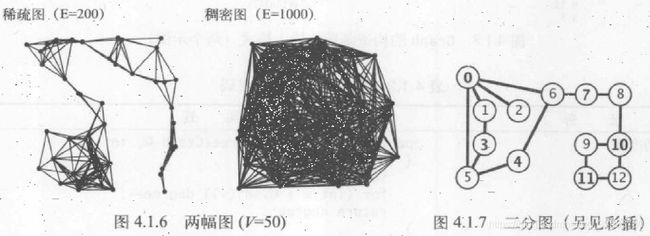
4.图的密度指已连接的顶点对占所有可能被连接的顶点对的比例。稀疏图中被连接的定点对较少,如果一幅图中不同的边的数量在顶点数V的一个小的常数倍以内,就认为该图是稀疏图,否则就是稠密图,如下所示:
二分图是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分,如上图右侧部分黑色加粗的结点是一个集合,不加粗的结点为另一个集合。
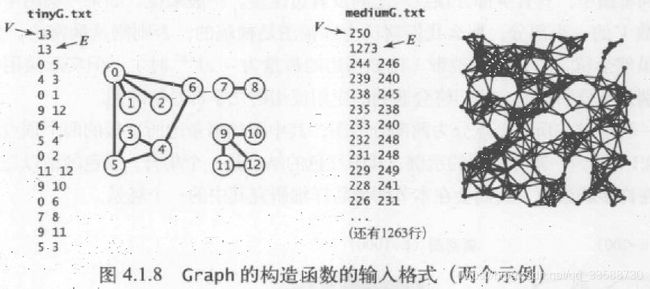
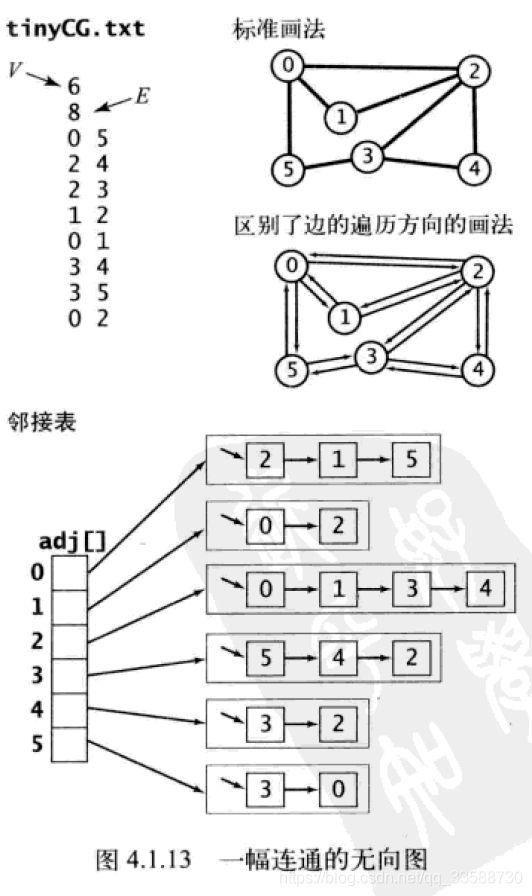
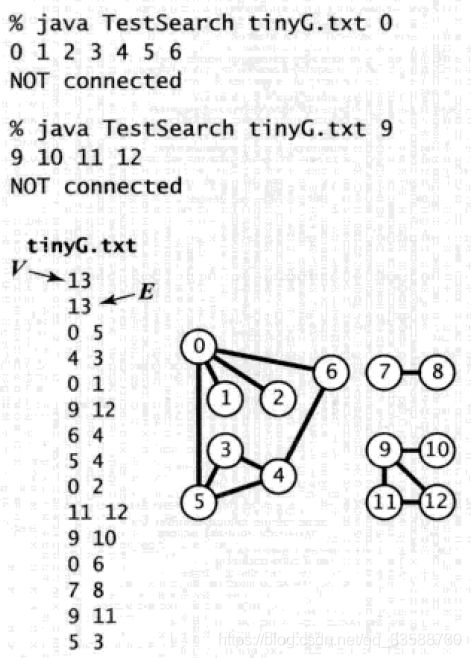
5.在书本提供的读取图的构造函数Graph(In in)中,输入in由2E+2个证书组成,首先是V顶点数,然后是E边数,然后是E对从0到V-1索引的整数,每个整数对都表示一条边,如下示例所示:
常用的图处理代码如下所示:
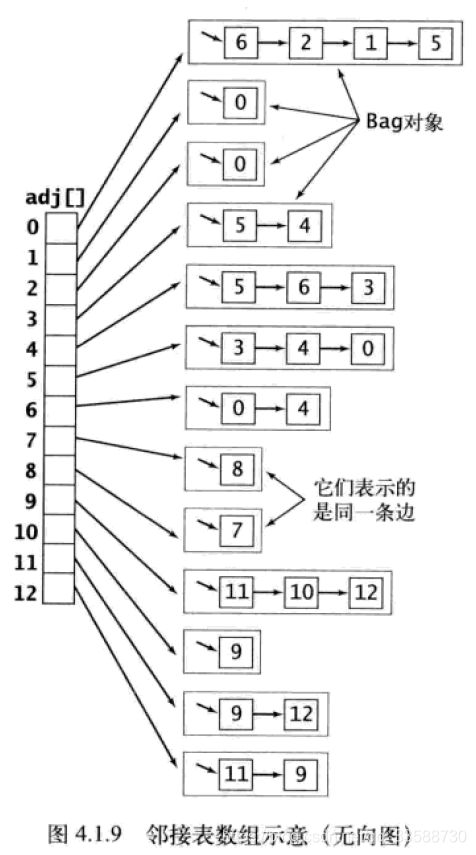
6.用邻接表数组这种特定的数据结构可以表示图,即使用一个以顶点为索引的列表数组,其中每个元素都是和该顶点相邻的顶点的列表,它可以满足图数据结构使用中的两个条件:(1)为应用中遇到的各种类型的图预留出足够空间;(2)Graph类的方法实现在速度上要够快,邻接表的数据结构如下所示:
邻接表将每个顶点的所有相邻顶点都保存在该顶点对应元素所指向的一个链表中,该链表可以使用Bag对象实现,因为Bag可以在常数时间内添加新的边或遍历任意顶点的所有相邻顶点,要添加一条连接v与w的边,需要将w添加到v的邻接表中,并将v添加到w的邻接表中,所以在邻接表的数据结构中每条边都会出现两次,下图中处理图输入文件tinyG.txt后就会形成上图那样的邻接表结构:
这种Graph类的实现性能有如下特点:(1)使用的空间与V+E成正比;(2)添加一条边所需的时间为常数;(3)遍历顶点v的所有相邻顶点所需的时间和v的度数成正比,处理每个相邻结点所需的时间为常数。
7.由于邻接表有链表结构,边的插入顺序决定了Graph的邻接表中顶点的出现顺序,多个不同的邻接表可能表示同一幅图,Graph类的代码实现如下所示:
package Chapter4_1Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
public class Graph { //图的实现
private final int V; //顶点数目
private int E; //边的数目
private Bag[] adj; //邻接表,adj[v]即和结点v相邻的所有顶点组成的链表
public Graph(int V){ //创建一个含有V个顶点但不含有边的图
this.V=V;
this.E=0;
adj=(Bag[]) new Bag[V]; //新建邻接表
for(int v=0;v();
}
public Graph(In in){ //从标准输入流in读入一幅图
this(in.readInt()); //读取V并将图初始化
int E=in.readInt(); //读取E
for(int i=0;i adj(int v){return adj[v];} //返回和结点v相邻的所有结点
public static int degree(Graph G,int v){ //计算结点v的度数
int degree=0;
for(int w:G.adj(v)) degree++; //结点v有一个邻接结点,度数就加1
return degree;
}
public static int maxDegree(Graph G){ //计算所有结点的最大度数
int max=0; //保存最大度数的值
for(int v=0;vmax) //遍历所有结点,如果有结点的度数比目前的最大值大,则覆盖最大值
max=degree(G,v);
return max;
}
public static double avgDegree(Graph G){return 2.0*G.E()/G.V();} //计算所有结点的平均度数,前面乘以2是因为两个结点有一条互相连接的边,互相都有1的度数,相当于有向图中的两条边
public static int numberOfSelfLoops(Graph G){ //计算自环的个数
int count=0;
for(int v=0;v 该Graph类的实现使用了一个由顶点作为数组索引的整形链表数组,每条边都会出现2次,即v与w连接时,w会出现在v索引的链表中,v也会出现在w索引的链表中。如果要实现删除一条边或者检查图是否含有边“v-w”的功能,需要用SET代替Bag来实现邻接表,此时该数据结构称为邻接集。常见几种图的数据结构实现的性能对比如下所示:
8.图的很多性质与路径有关,为了理解路径搜索,可以举个走迷宫的例子,名为Tremaux搜索,即一个人走迷宫时握着绳子,在第一次走过的路径中铺绳子,遇到走过的路径(看到绳子)就后退并回收绳子到上一个分岔口,如果回退到的分岔口已没有可走的通道时继续回退一个岔路口,如下所示:
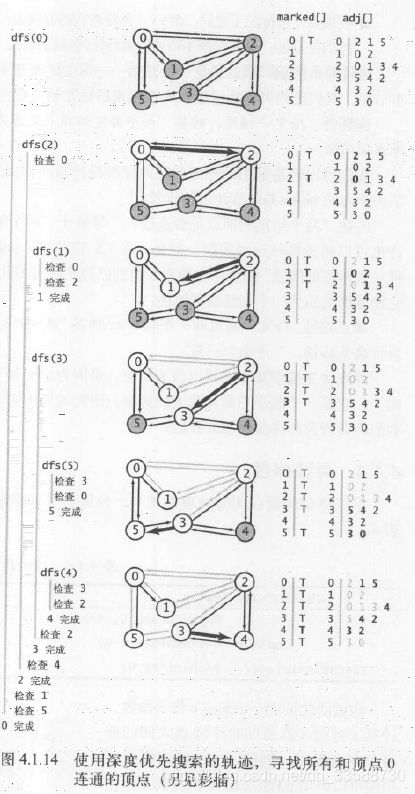
和上面的迷宫寻路类似,真正搜索连通图的递归算法会调用一个递归方法来遍历所有顶点,在访问一个顶点时将它标记为已访问,并递归地访问它所有未被标记过的邻居顶点,这种方法称为深度优先搜索(DFS),可用于检测图的连通性,以及是否存在连接两个结点的一条路径,代码如下所示:
package Chapter4_1Text;
public class DepthFirstSearch { //搜索结点连通性的类,作为TestSearch的辅助类
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int count; //与起点s连通的顶点总数
public DepthFirstSearch(Graph G,int s){
marked=new boolean[G.V()]; //创建一个布尔值数组,元素数量为图中的结点数量,初始化数组中每个位置都为false
dfs(G,s); //从起点s开始深度优先搜索
}
private void dfs(Graph G,int v){
marked[v]=true; //经过的结点设置为已访问过
count++; //可以到达的结点数加1
for(int w:G.adj(v)) //遍历当前结点的所有邻接结点,如果有邻接结点没有被访问过,就从该邻接结点继续进行递归搜索
if(!marked[w]) dfs(G,w);
}
public boolean marked(int w){return marked[w];} //结点w和起点s是否连通,即从起点s能不能访问到w
public int count(){return count;} //与起点s连通的结点总数
}
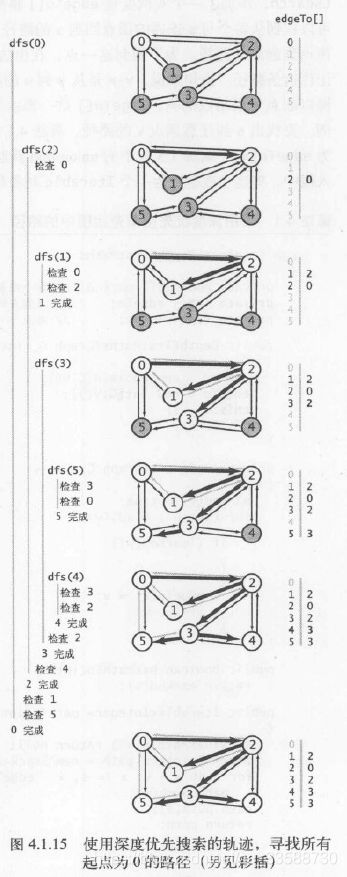
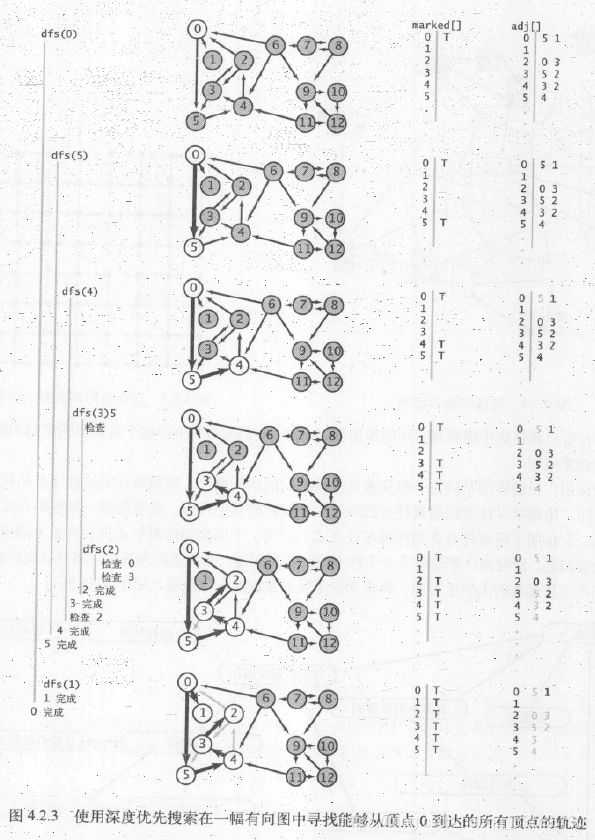
下面的图例可以说明深度优先搜索算法的原理:
在这张图中,深度优先搜索算法实际上每条边都会被访问两次,且在第2次时发现该顶点已经被标记过,意味着深度优先搜索的轨迹比实际路径数量多一倍。深度优先搜索的轨迹例子如下图所示,DFS标记与起点连通的所有结点所需时间与结点的度数之和成正比:
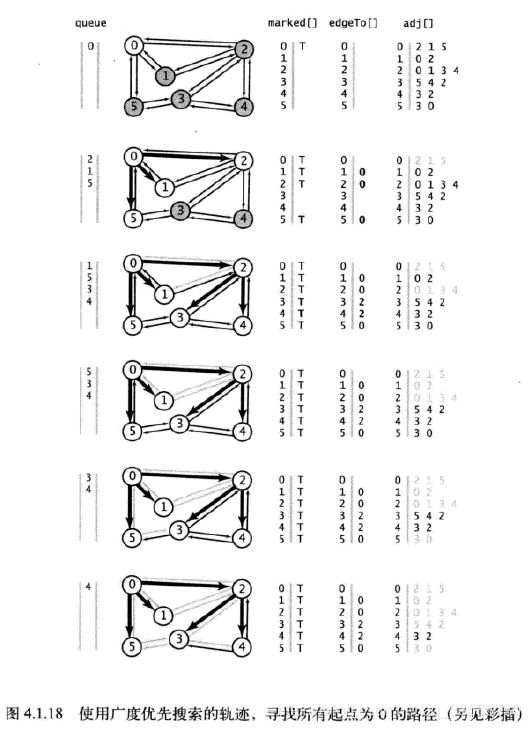
上图表示的搜索步骤如下:
(1)首先从起点0开始搜索,2是0的邻接表(链表结构)的第一个元素且没被标记过,所以递归调用dfs(2),系统会将顶点0和0的邻接表的当前位置压入栈中。
(2)顶点0是2的邻接表的第一个元素且已被标记过,dfs()会跳过0,下面顶点1是2的邻接表的第二个元素且未被标记,因此递归调用dfs(1)。
(3)dfs(1)发现顶点1连接的所有结点都都标记过了,于是回退直接返回到结点2(就像上面走迷宫时的回退),下一条被检查的边是2-3,因此递归调用dfs(3)。
(4)顶点5是3的邻接表的第一个元素且未被标记,因此递归调用dfs(5)。
(5)顶点5的邻接表中所有顶点(3和0)都已被标记过,不需要再递归,回退到结点3。
(6)顶点4是3的邻接表的下一个元素且未被标记,所以递归调用dfs(4),这是最后一个需要被标记的结点。
(7)在顶点4被标记后,dfs(4)会检查它的邻接表,然后回退检查3的邻接表,再回退检查2的邻接表,最后是0的,所有顶点已被标记。
9.下面的代码接受命令行中的一个输入流名称和起始(source)节点的编号,从输入流读取一幅图,并根据该图和起始结点创建一个DepthFirstSearch对象,然后用marked()方法打印图中和该起点连通的所有顶点:
package Chapter4_1Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
public class TestSearch { //读取图并测试结点间的连通性
public static void main(String[] args){
Graph G=new Graph(new In(args[0])); //从输入流中读取命令行第一个参数指定的图结构文件
int s=Integer.parseInt(args[1]); //读取命令行第二个参数指定的起点结点
DepthFirstSearch search =new DepthFirstSearch(G,s); //该对象用于找到和起点s连通的所有顶点
for(int v=0;v该代码的执行结果如下所示:
10.下面的代码通过深度优先搜索算法来寻找从起点s到结点v的路径:
package Chapter4_1Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;
public class DepthFirstPaths { //基于深度优先搜索寻找图中从给定起点s到它连通的所有结点的路径
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int[] edgeTo; //从起点到一个结点的已知路径上的最后一个结点,相当于走迷宫例子中绳子记录路径的作用,通过该数组可以找到从每个与s连通的结点回到s的路径,是一棵用父节点链接表示的以s为根且含有所有与s连通的结点的树
private final int s; //起点
public DepthFirstPaths(Graph G,int s){
marked=new boolean[G.V()]; //创建一个布尔值数组,元素数量为图中的结点数量,初始化数组中每个位置都为false
edgeTo=new int[G.V()];
this.s=s;
dfs(G,s);
}
private void dfs(Graph G,int v){
marked[v]=true; //经过的结点设置为已访问过
for(int w:G.adj(v)) //遍历所有邻接结点
if(!marked[w]){
//如果有邻接结点没有访问过,则记录到该邻接结点为止的路径,方式是例如边“v-w”第一次访问到w时,将edgeTo[w]设为v,即“v-w”是从s到w路径上最后一条已知的边,edgeTo[]是一棵由父结点链接表示的树
edgeTo[w]=v;
dfs(G,w);
}
}
public boolean hasPathTo(int v){return marked[v];} //是否存在从s到v的路径
public Iterable pathTo(int v){ //用可遍历的迭代器输出s到v的路径,如果不存在则返回null
if(!hasPathTo(v)) return null;
Stack path=new Stack();
for(int x=v;x!=s;x=edgeTo[x]) //从树的底部结点v开始从底向上遍历整棵树,因为edgeTo[]中放置的元素是各索引表示的结点的父结点
path.push(x); //在到达树根s之前,遇到的所有结点都压入栈中
path.push(s); //最后只剩下起点s,压入栈中后形成一棵以起点s为根节点的路径树
return path;
}
public static void main(String[] args){
Graph G=new Graph(new In(args[0])); //从输入流中读取命令行第一个参数指定的图结构文件
int s=Integer.parseInt(args[1]); //读取命令行第二个参数指定的起点结点
DepthFirstPaths search=new DepthFirstPaths(G,s); //该对象用于找到所有和起点s连通的路径
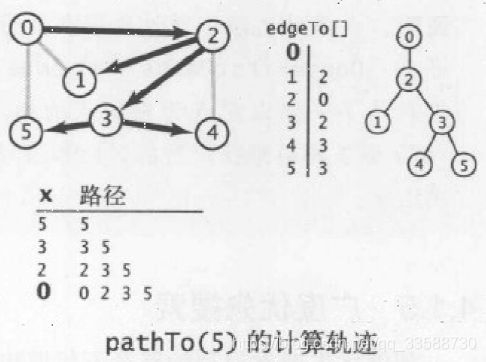
for(int v=0;v 其中pathTo()函数的计算轨迹如下所示,edgeTo[]数组中对应索引处的元素就是索引数字对应结点的父节点,路径就是一个名为path的栈,从最终到达的结点开始从底向上不断加入父节点直到起点,这样相反方向的入栈,出栈时就是从起点到达最终结点的顺序:
上面深度优先搜索寻找所有起点为0的路径的轨迹如下所示,DFS得到从给定起点到任意标记顶点的路径所需时间与路径长度成正比,edgeTo[]数组元素的填入过程十分直观:
运行代码后的结果输出如下所示:
11.深度优先搜索(DFS)在寻找最短路径上没什么作为,因为它遍历整个图的顺序和找出最短路径的目标没有任何关系。为了寻找从起点s到给定结点v的最短路径,真正有用的方法叫广度优先搜索(BFS)。BFS的思路是从s开始,在所有距离一条边的可到达结点中寻找v,如果没找到就从距离两条边的可到达节点中寻找,以此类推。DFS像是一个人在走迷宫,而BFS更像是一组人在一起朝各个方向走迷宫,每个人都有自己的绳子,出现新岔路时,一组人会分裂为两组人搜索,当两组人相遇时会合二为一(并继续使用先到达者的绳子),该类比示意图如下所示:
在DFS中,使用了栈的LIFO(后进先出)规则来实现从待搜索的通道中选择最晚遇到的那条,而在BFS中,是按照与起点的距离的顺序来遍历所有顶点的,因此要把栈换成FIFO队列,即从待搜索的通道中选择最早遇到的那条。该队列保存所有已被标记过但其邻接表还未被检查过的顶点。先将起点加入队列,然后重复以下步骤直到队列为空:(1)取队列中的下一个顶点v并标记它;(2)将与v相邻的所有未被标记过的顶点加入队列。BFS的代码实现如下所示:
package Chapter4_1Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Queue;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;
public class BreadthFirstPaths { //使用广度优先搜索(BFS)查找图中的最短路径
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int[] edgeTo; //从起点到一个结点的已知路径上的最后一个结点,相当于走迷宫例子中绳子记录路径的作用,通过该数组可以找到从每个与s连通的结点回到s的最短路径,是一棵用父节点链接表示的以s为根且含有所有与s连通的结点的树
private final int s; //起点
public BreadthFirstPaths(Graph G,int s){
marked=new boolean[G.V()]; //创建一个布尔值数组,元素数量为图中的结点数量,初始化数组中每个位置都为false
edgeTo=new int[G.V()];
this.s=s;
bfs(G,s);
}
private void bfs(Graph G,int s){
Queue queue=new Queue();
marked[s]=true; //经过的结点设置为已访问过
queue.enqueue(s); //将途径的结点加入队列
while(!queue.isEmpty()){
int v=queue.dequeue(); //从队列中出列下一个顶点
for(int w:G.adj(v)) //遍历所有邻接结点
if(!marked[w]){
//如果有邻接结点没有访问过,则记录到该邻接结点为止的路径,方式是例如边“v-w”第一次访问到w时,将edgeTo[w]设为v,即“v-w”是从s到w路径上最后一条已知的边,edgeTo[]是一棵由父结点链接表示的树,代表s到每个s连通的结点的最短路径
edgeTo[w]=v;
marked[w]=true; //标记它,因为最短路径已知
queue.enqueue(w); //将它添加到队列中
}
}
}
public boolean hasPathTo(int v){return marked[v];} //是否存在从s到v的路径
public Iterable pathTo(int v){ //用可遍历的迭代器输出s到v的路径,如果不存在则返回null
if(!hasPathTo(v)) return null;
Stack path=new Stack();
for(int x=v;x!=s;x=edgeTo[x]) //从树的底部结点v开始从底向上遍历整棵树,因为edgeTo[]中放置的元素是各索引表示的结点的父结点
path.push(x); //在到达树根s之前,遇到的所有结点都压入栈中
path.push(s); //最后只剩下起点s,压入栈中后形成一棵以起点s为根节点的路径树
return path;
}
public static void main(String[] args){
Graph G=new Graph(new In(args[0])); //从输入流中读取命令行第一个参数指定的图结构文件
int s=Integer.parseInt(args[1]); //读取命令行第二个参数指定的起点结点
BreadthFirstPaths search=new BreadthFirstPaths(G,s); //该对象用于找到所有和起点s连通的最短路径
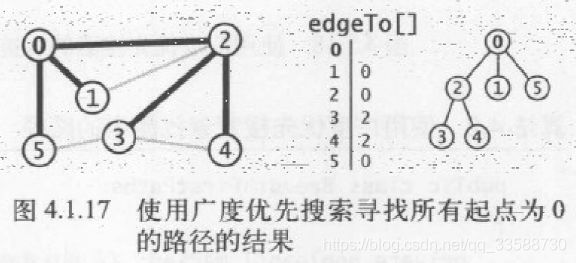
for(int v=0;v 下面两个示意图表示了用BFS搜索最短路径时的轨迹和步骤,BFS所需时间在最坏情况下与V+E成正比:
(1)起点0被加入队列,然后循环开始搜索。
(2)从队列删去顶点0并将它的相邻顶点2、1和5加入队列中,标记它们并分别将它们在edgeTo[]中的值设为0。
(3)从队列删去顶点2并检查它的相邻顶点0和1,发现两者都已被标记。将相邻顶点3和4加入队列,标记它们并分别将它们在edgeTo[]中的值设为2。
(4)从队列删去顶点1并检查相邻顶点0和2,发现已被标记。
(5)从队列删去顶点5并检查相邻顶点3和0,发现已被标记。
(6)从队列删去顶点3并检查相邻顶点5、4和2,发现已被标记。
(7)从队列删去顶点4并检查相邻顶点3和2,发现已被标记。
在上面的例子中,edgeTo[]数组在第3步以后就已经完成,与DFS相同,一旦所有结点已经被标记,剩下的计算工资就只是在检查连接到各个已标记结点的边。上面代码的执行结果如下所示:
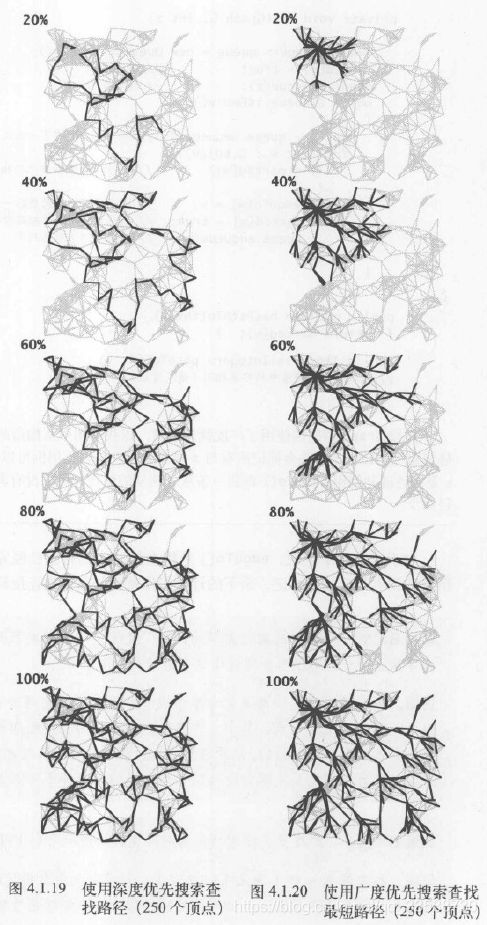
12.DFS与BFS在实现时都会先将起点存入一个数据结构中,然后重复以下步骤直到数据结构被清空:(1)取其中的下一个顶点并标记它;(2)将v所有相邻但又未标记的顶点加入数据结构。两个算法的不同之处只在于从数据结构中获取下一个顶点的规则,BFS是最早加入的顶点,而DFS是最晚加入的顶点。两种算法的搜索路径差异如下图所示:
从上图可以看到,DFS不断深入图中并在栈中保存所有分叉顶点;而BFS像扇面一样扫描图,用一个队列保存访问过的最前端顶点。DFS搜索一幅图的方式是寻找离起点更远的顶点,只在碰到死胡同时才访问近处的顶点;而BFS会首先覆盖起点附近的顶点,只在临近所有顶点都被访问才向深处前进。
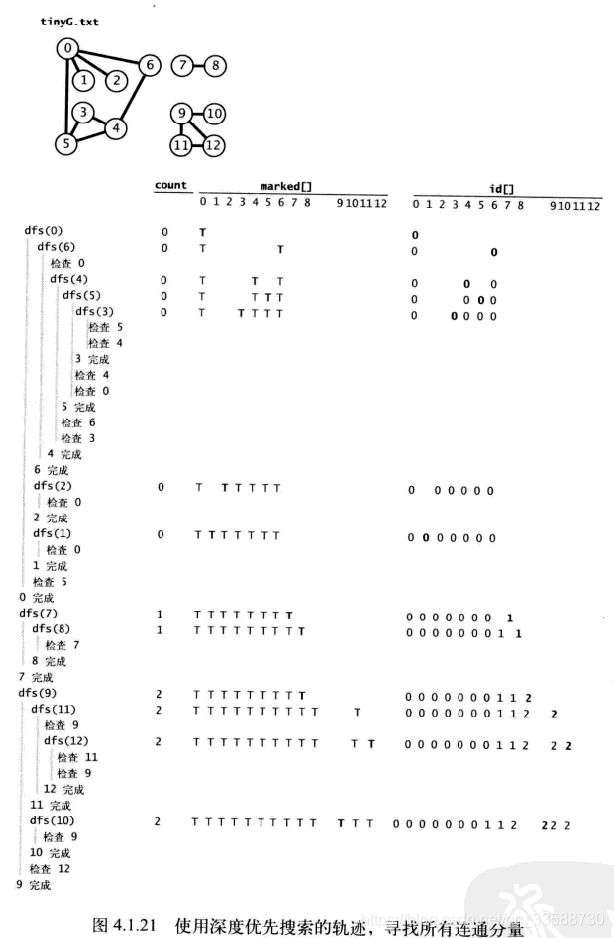
13.DFS的其中一个应用就是找出一幅图的所有连通分量,连通分量(Connected Component)就是图中的极大连通子图,即每个图中可能有几片区域,这几片区域内各自的结点互相连通,但是几个区域间不连通。完全连通图的连通分量只有1个,而非连通的图有多个连通分量。查找并打印一张图中所有连通分量的代码如下所示:
package Chapter4_1Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
public class CC { //使用深度优先搜索(DFS)找出图中的所有连通分量(即图中有几片互相连通的结点区域,但这几个区域之间不连通)
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int[] id; //以结点ID作为索引的数组,存储对应结点所属的连通分量ID,例如如果结点v属于第i个连通分量,id[v]的值为i
private int count; //连通区域的数量(即连通分量数)
public CC(Graph G){
marked=new boolean[G.V()];
id=new int[G.V()];
for(int s=0;s[] components; //存储每个子连通区域(连通分量)的所有结点
components=(Bag[]) new Bag[M];
for(int i=0;i();
for(int v=0;v 上述代码的搜索轨迹与运行结果如下所示,DFS预处理图结构所需的时间和空间与V+E成正比且在常数时间内处理图的连通性查询:
14.检测一幅图是否是有环图的代码如下所示:
package Chapter4_1Text;
public class Cycle { //检测图G是否是有环图(假设不存在自环和平行边)
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private boolean hasCycle;
public Cycle(Graph G){
marked=new boolean[G.V()];
for(int s=0;s检测一幅图是否是二分图的代码如下所示:
package Chapter4_1Text;
public class TwoColor { //检测一幅图是否是二分图,即用两种颜色标记所有结点,使任意一条边的两个端点的颜色都不相同
private boolean[] marked; //用于标记结点是否与起点s连通,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private boolean[] color; //标记各结点的两种颜色
private boolean isTwoColorable=true; //标记是否是二分图
public TwoColor(Graph G){
marked=new boolean[G.V()];
color=new boolean[G.V()];
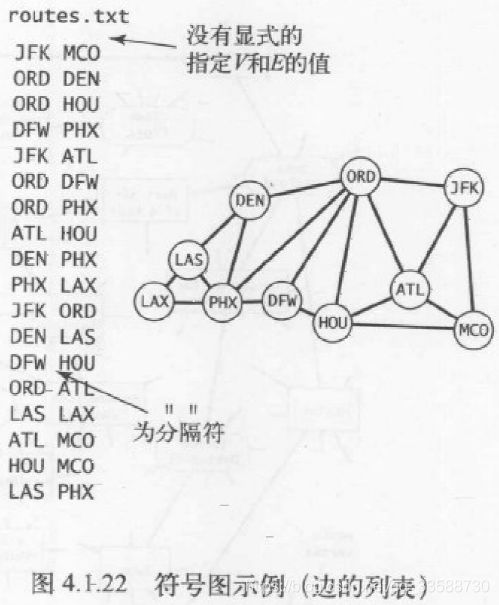
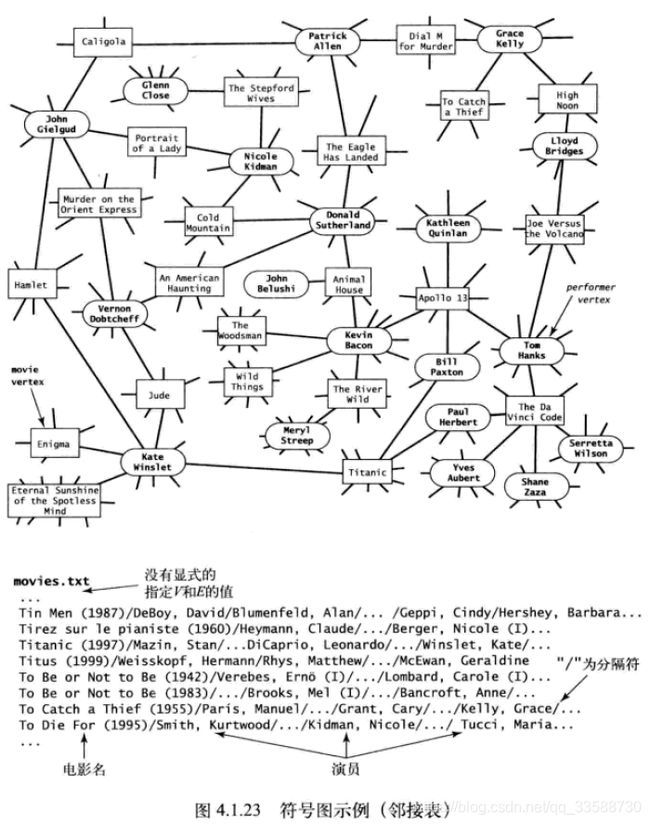
for(int s=0;s15.在现实应用中,图都是用文件或者网页定义的,使用的是字符串而不是整数来表示顶点,此时这种图需要用符号图来表示,这种图的顶点名为字符串,每一行都表示一组边的集合,每条边都连接着这一行用分隔符隔开的多个顶点名称,且顶点数V和边数E并没有显式指定,如下面的例子所示,该文件表示一个运输路线图,每个顶点是美国机场代码,边表示顶点间的航线:
另一个例子是互联网电影数据库,该文件的每一行列出一个电影名及其演员,这两者都是顶点,所以是一个二分图,即电影和电影以及演员和演员之间不相连,只是电影和演员连接。作为一个二分图,它的性质可以轻松实现反向索引的功能,即原本的movies.txt的格式是为了方便根据电影名找到相关演员,而二分图可以通过演员反向找到他参加的所有电影,如下所示:
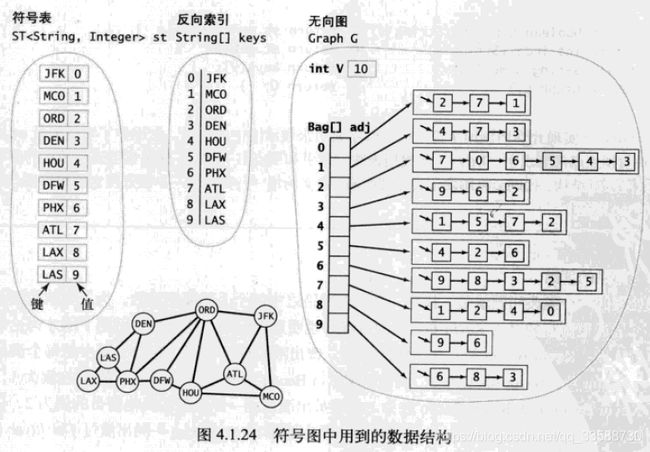
符号图的代码实例如下所示:
package Chapter4_1Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.ST;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class SymbolGraph { //符号图,使用字符串代替数字索引来表示图中的结点
private ST st; //符号图的数据结构,一个符号表,键为结点名,值为结点的索引
private String[] keys; //用作反向索引,存放每个结点索引对应的结点名
private Graph G; //图对象,使用索引来引用图中的结点
public SymbolGraph(String stream,String sp){ //根据stream指定的文件来构造图,使用sp指定的分隔符来区分结点名
st=new ST();
In in=new In(stream); //第一遍读取图,因为构造Graph对象需要获取结点总数
while(in.hasNextLine()){
String[] a=in.readLine().split(sp); //通过输入流读取字符串,并用指定分隔符分割结点名
for(int i=0;i 过去的Graph图对象需要明确指定结点数V和边数E,但这在现实应用中会不方便,会无法在图文件中灵活增删条目,而使用SymbolGraph这种符号图对象,不需要指定V和E,就不需要费心思在增删条目的时候时刻维护这两个值。符号图的数据结构如下所示:
运行上面代码的结果如下所示:
16.图处理的一个常见场景就是找到社交网络中两个人间隔的度数,例如电影和演员的关系图movie.txt中,某个演员A演过很多电影,自己的度数为0,设与A演过同一部电影的演员B度数为1,与B合作同一部电影的演员C没有与A合作过,所以C的度数为2,以此类推。此时,需要有一个程序能根据度数找到从一个顶点到达另一个顶点的最短路径,代码如下所示:
package Chapter4_1Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class DegreesOfSeparation { //根据结点的度数来找到一个结点通向另一个结点的最短路径
public static void main(String[] args){
SymbolGraph sg=new SymbolGraph(args[0],args[1]); //根据命令行第1个参数指定输入文件,第2个参数指定分隔符来构造图文件的数据结构
Graph G=sg.G(); //初始化图对象
String source=args[2]; //命令行第3个参数指定起点
if(!sg.contains(source)){
StdOut.println(source+"not in database.");
return;
}
int s=sg.index(source); //获取起点对应的索引ID
BreadthFirstPaths bfs=new BreadthFirstPaths(G,s); //利用BFS查找最短路径
while(!StdIn.isEmpty()){
String sink=StdIn.readLine(); //从标准输入流命令行中读取目的结点
if(sg.contains(sink)){
int t=sg.index(sink); //获取目的结点的索引ID
if(bfs.hasPathTo(t)) //如果能够找到从起点通向目的结点的最短路径,打印经过的结点名
for(int v:bfs.pathTo(t))
StdOut.println(" "+sg.name(v));
else StdOut.println("Not connected");
}else StdOut.println("Not in database.");
}
}
}
二、有向图
17.在有向图中,边是单向的,因此有向图中结点v能到达w不意味着w也能到达v。现实中的典型有向图结构如下所示:
在一幅有向图中,一个顶点的出度为该顶点指出的边的总数,入度为指向该顶点的边的总数,一条有向边的第一个顶点为这条边的头,第二个顶点为尾。尽管有向图看起来比无向图复杂,但代码上数据结构的表示甚至更加简单,如下所示:
package Chapter4_2High;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
//用于Exercise 4.2.30的依赖类
public class Digraph { //有向图的数据结构
private final int V; //图中的结点数
private int E; //图中的连接边数
private Bag[] adj; //元素索引为结点ID,数组元素为对应索引结点所连接的邻接结点集合
public Digraph(int V){ //创建一幅含有V个结点但没有边的有向图
this.V=V;
this.E=0;
adj=(Bag[]) new Bag[V]; //存放V个结点的邻接结点集合
for(int v=0;v(); //初始化每个结点的邻接结点集合
}
public Digraph(In in){ //从输入流中读取图文件并构造有向图
this(in.readInt()); //读取V并将图初始化
int E=in.readInt(); //读取E
for(int i=0;i reverse=new Stack<>();
for(int i:G.adj(v)){
reverse.push(i); //将结点v的所有邻接结点放入栈中
}
for(int i:reverse){ //将栈中的邻接结点放入结点v的邻接数组中
adj[v].add(i);
}
}
}
public Digraph() {
V = 0;
}
public int V(){return V;} //返回图中结点总数
public int E(){return E;} //返回图中边的总数
public void addEdge(int v,int w){ //添加一条结点v指向结点w的边
adj[v].add(w); //邻接结点集合数组中在结点v的索引上加入w
E++; //增加边的总数
}
public Iterable adj(int v){return adj[v];} //返回结点v指向的所有邻接结点
public Digraph reverse(){ //返回图的反向图,即所有边的方向反转
Digraph R=new Digraph(V); //建立一个没有边的有向图
for(int v=0;v 如果要实现符号表格式如SymbolGraph类一样的数据结构,只需要把SymbolGraph类中的Graph类全都替换成Digraph就行。有向图的数据结构图示如下所示:
18.在有向图中使用深度优先搜索(DFS)来检查某个结点是否可达的算法如下所示:
package Chapter4_2Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
public class DirectedDFS { //使用DFS在有向图中判断给定的一个或者一组结点能到达哪些其他结点
private boolean[] marked; //用于标记结点是否由起点s可达,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
public DirectedDFS(Digraph G,int s){ //从图G中找到从结点s可达的所有结点
marked=new boolean[G.V()];
dfs(G,s);
}
public DirectedDFS(Digraph G,Iterable sources){ //从图G中找到从结点集合sources中的所有结点,它们可到达的所有结点
marked=new boolean[G.V()];
for(int s:sources)
if(!marked[s]) dfs(G,s);
}
private void dfs(Digraph G,int v){ //DFS核心方法
marked[v]=true;
for(int w:G.adj(v)) //递归遍历没有到达过的邻接结点
if(!marked[w]) dfs(G,w);
}
public boolean marked(int v){return marked[v];} //从起点s是否可以到达结点v
public static void main(String[] args){
Digraph G=new Digraph(new In(args[0])); //从命令行中第1个参数指定图输入文件
Bag sources=new Bag();
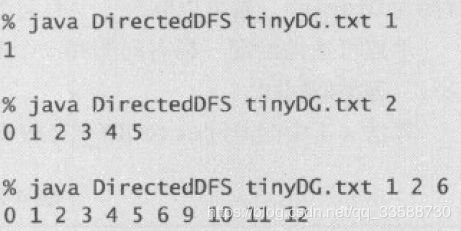
for(int i=1;i 上面代码的执行结果与DFS轨迹如下所示,DFS标记由一个集合中的顶点可达的所有顶点所需时间与所有被标记顶点的出度之和成正比:
上述有向图多点可达性的其中一个实际应用是JVM的内存管理垃圾回收系统,其中一个顶点表示一个对象,一条有向边表示一个对象对另一个对象的引用,JVM会周期性运行一个类似DirectedDFS的有向图可达性算法来标记所有能访问到的对象,清理无法访问的对象。在无向图部分中的DepthFirstPaths和BreadthFirstPaths寻找路径算法里,只需要把Graph对象换成DiGraph对象就能处理有向图的最短路径问题。
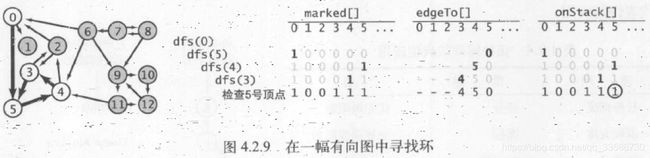
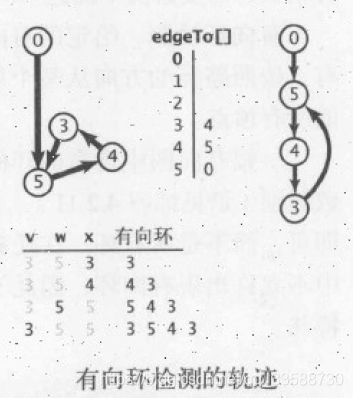
19.在实际应用中,把一些问题例如任务调度和课程安排等作为有向图进行考虑很重要,这些问题不允许出现有向环,即任务调度中任务x必须在任务y之前完成,任务y必须在任务z之前完成,但是任务z必须在任务x之前完成,这种无解情况是不允许出现的,因此会用到有向环检测,希望该有向图是有向无环图(DAG)。有向环检测的代码如下所示:
package Chapter4_2Text;
import edu.princeton.cs.algs4.Stack;
public class DirectedCycle { //在有向图中利用DFS寻找有向环
private boolean[] marked; //用于标记结点是否由起点s可达,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int[] edgeTo; //从起点到一个结点的已知路径上的最后一个结点,相当于走迷宫例子中绳子记录路径的作用,通过该数组可以找到从每个由s可达的结点的路径,是一棵以s为根且含有所有由s可达的结点的树链
private Stack cycle; //存放有向环中的所有顶点(如果存在)
private boolean[] onStack; //递归调用dfs()期间一条有向路径栈上的所有结点,记录了一条从起点到v的有向路径,当找到一条边v->w且w在栈中时,就找到了一个有向环
public DirectedCycle(Digraph G){
onStack=new boolean[G.V()];
edgeTo=new int[G.V()];
marked=new boolean[G.V()];
for(int v=0;vw”第一次访问到w时,将edgeTo[w]设为v,即“v->w”是从起点s到w路径上最后一条已知的边,edgeTo[]是一棵由父结点链接表示的树
edgeTo[w]=v;
dfs(G,w);
}else if(onStack[w]){ //如果DFS路径上某个结点w之前被访问过,说明出现了环
cycle=new Stack();
for(int x=v;x!=w;x=edgeTo[x]) //将环入口结点w的上一个结点v,到结点w的所有路径上结点都压入存放有向环结点的栈中
cycle.push(x); //栈中先放入的是当前结点的父节点,因为edgeTo[]数组放置的元素就是当前索引结点的上一个结点,这样最后栈顶层是环入口结点的下一个结点
cycle.push(w);
cycle.push(v);
}
}
onStack[v]=false; //当前路径的DFS递归调用结束,该结点可用于其他路径的递归
}
public boolean hasCycle(){return cycle!=null;} //判断是否存在有向环,即存放有向环结点的栈中是否有元素
public Iterable cycle(){return cycle;}
}
20.在现实的调度问题中,不同的任务有不同的优先级限制,可以利用有向无环图来计算所有任务结点的拓扑顺序,代码如下所示:
package Chapter4_2Text;
import edu.princeton.cs.algs4.Queue;
import edu.princeton.cs.algs4.Stack;
public class DepthFirstOrder { //有向图中基于DFS的结点排序(可用于任务调度中的优先级排序)
private boolean[] marked; //用于标记结点是否由起点s可达,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private Queue pre; //所有结点的前序排列,即递归搜索之前将结点加入队列
private Queue post; //所有结点的后续排列,即递归搜索之后将结点加入队列
private Stack reversePost; //所有结点的逆后序排列,即递归搜索之后将结点压入栈
public DepthFirstOrder(Digraph G){
pre=new Queue();
post=new Queue();
reversePost=new Stack();
marked=new boolean[G.V()];
for(int v=0;v pre(){return pre;}
public Iterable post(){return post;}
public Iterable reversePost(){return reversePost;}
}
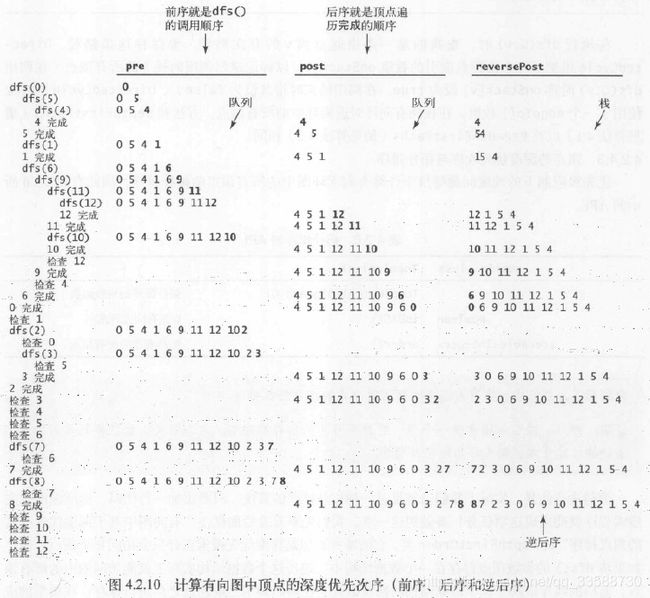
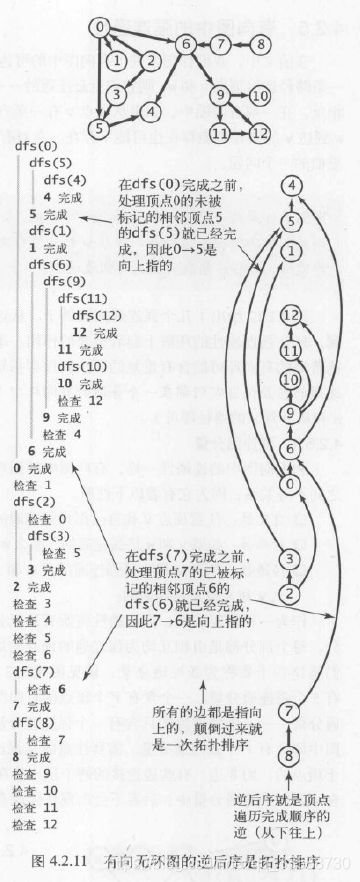
上述代码可以用各种顺序遍历DFS经过的所有结点,排序后图结点的遍历顺序取决于三种排序方式,分别是前序、后序和逆后序。三种排列顺序的轨迹如下所示:
将符号有向图SymbolDigraph利用DepthFirstOrder中的DFS进行拓扑排序的代码如下所示:
package Chapter4_2Text;
import edu.princeton.cs.algs4.StdOut;
public class Topological { //结点的拓扑排序
private Iterable order; //结点的拓扑顺序
public Topological(Digraph G){
DirectedCycle cyclefinder=new DirectedCycle(G);
if(!cyclefinder.hasCycle()){
DepthFirstOrder dfs=new DepthFirstOrder(G);
order=dfs.reversePost(); //使用逆后序的排列顺序
}
}
public Iterable order(){return order;} //返回拓扑有序的所有结点
public boolean isDAG(){return order!=null;} //是否是有向无环图
public static void main(String[] args){
String filename=args[0]; //从命令行第一个参数指定读取的文件
String separator=args[1]; //从命令行第二个参数指定元素分隔符
SymbolDigraph sg=new SymbolDigraph(filename,separator);
Topological top=new Topological(sg.G()); //从符号有向图对象中构造图
for(int v:top.order()) //以逆后序的顺序遍历输出结点名
StdOut.println(sg.name(v));
}
}
一幅有向无环图的拓扑顺序一定是所有结点的逆后序排列,因为dfs()的递归调用中,后被递归的结点一定比先被递归的结点更先return,只有通过栈的逆后序排列才能使输出时先递归的结点排在后递归的结点之前。上面代码的运行轨迹如下所示,其中计算生物学(4)为栈底,微积分(8)为栈顶,使用DFS进行拓扑排序所需时间与V+E成正比:
根据上面的轨迹,上面代码的运行结果如下所示:
在实际应用中,拓扑排序和有向环检测总会一起出现,因为有向环检测是拓扑排序的前提,在任务调度应用中,如果出现一个环说明严重的安排错误,因此解决任务调度问题一般需要三步:(1)指明任务和优先级条件。(2)不断检测并去除环,确保方案可行。(3)使用拓扑排序来解决调度问题。所以,调度方案变动之后必须重新进行有向环检测与拓扑排序。
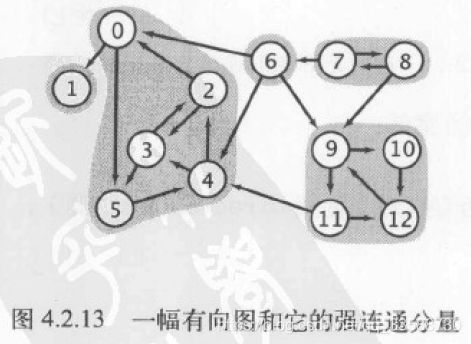
21.在有向图中,如果两个顶点v和w是互相可达的,就称它们是强连通的,但是出现强连通说明图中出现了有向环。和无向图中的连通分量(多个结点互相连通的子图)类似,多个互相强连通的有向图结点会组成强连通分量。强连通分量具有以下性质:(1)自反性,任意顶点v与自己强连通。(2)对称性:如果v和w强连通,那么w也和v强连通。(3)传递性:如果v和w强连通且w和x强连通,则v和x也强连通。
强连通的结点之间等价,所有结点互相都强连通的图称为强连通图,它只有一个强连通分量,而一个含有V个顶点的有向无环图中含有V个强连通分量。强连通分量的定义基于顶点而不是边,有些边连接的两个顶点在同一个强连通分量中,但有些边连接的两个顶点则在不同的强连通分量中,这种顶点不会出现在任何有向环之中,如下面的结点1和6:
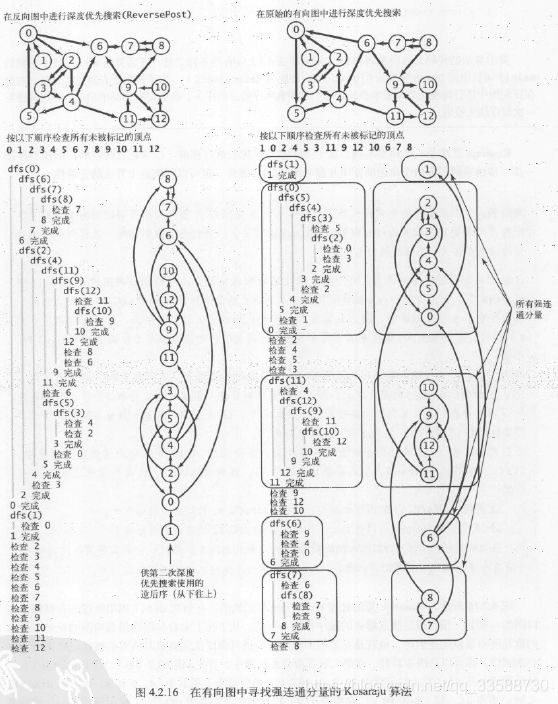
强连通分量十分有用,例如可以帮助教科书作者将哪些话题归为一类,帮助程序员组织程序模块,帮助网络工程师将网络中的网页分为多个大小合适的部分进行分别处理等。与之前计算无向图连通分量的CC类相似,计算有向图中强连通分量的Kosaraju算法如下所示:
package Chapter4_2Text;
public class KosarajuSCC { //计算有向图中强连通分量(多个互相强连通的有向图结点组成的子图)的Kosaraju算法
private boolean[] marked; //用于标记结点是否由起点s可达,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private int[] id; //结点所属强连通分量的标识符(ID)
private int count; //强连通分量的数量
public KosarajuSCC(Digraph G){
marked=new boolean[G.V()];
id=new int[G.V()];
//计算图的反向图,即后序顺序的拓扑排列,该对象在构造反向图之前已经形成了正常顺序的有向图,原图按正常顺序DFS能证明存在一条从s到v的路径
DepthFirstOrder order=new DepthFirstOrder(G.reverse());
//在后序顺序拓扑(反向图)的基础上再遍历它的逆后序,原图正向遍历存在s到v的路径,如果是对反向图进行逆后序的DFS可以证明原图存在一条从v到s的路径,即反向图中存在s到v的路径
for(int s:order.reversePost())
if(!marked[s]){
dfs(G,s);
count++; //一轮DFS递归结束后,所有处于同一轮递归中被访问到的结点都属于同一个强连通分量,因此个数加1
}
}
private void dfs(Digraph G,int v){
marked[v]=true;
id[v]=count; //给同一轮DFS递归访问到的结点加上相同的强连通分量ID
for(int w:G.adj(v)) //继续在同一轮DFS递归中遍历未访问过的邻接结点
if(!marked[w])
dfs(G,w);
}
public boolean stronglyConnected(int v,int w){return id[v]==id[w];} //结点v和w是否强连通,就看他们所属的强连通分量ID是否相同
public int id(int v){return id[v];}
public int count(){return count;}
}
上述算法的DFS轨迹如下图左侧所示,右侧是原图正常顺序DFS的轨迹,该算法的图构造预处理所需时间和空间与V+E成正比且支持常数时间的有向图强连通性查询:
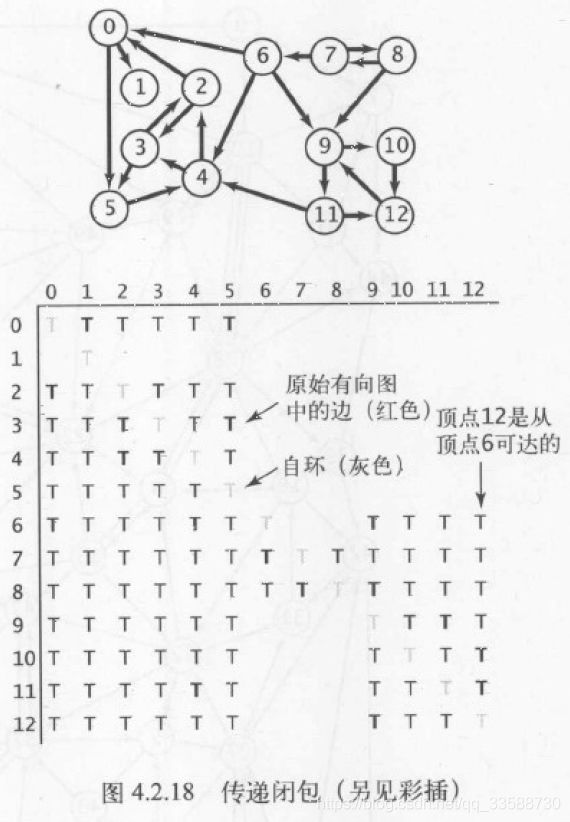
22.有向图G的传递闭包是一种布尔值矩阵,它表示了G中的结点之间的可达性,其中v行w列的值为true意味着结点w能够从v可达,如下所示:
利用DFS计算这种结点可达性的传递闭包代码如下所示:
package Chapter4_2Text;
public class TransitiveClosure { //计算结点可达性的传递闭包
private DirectedDFS[] all;
TransitiveClosure(Digraph G){
all=new DirectedDFS[G.V()];
for(int v=0;v上述代码对于稀疏图和稠密图都适用,但不适合实际应用中的大型有向图,因为构造函数所需空间与V^2成正比,所需时间和V(V+E)成正比,共有V个DirectedDFS对象,每个对象所需空间都与V成正比(包含大小为V的marked[]数组并检查E条边)。尽管预处理的开销较大,但是查询可达性的方法reachable()只需要常数时间处理。
三、最小生成树
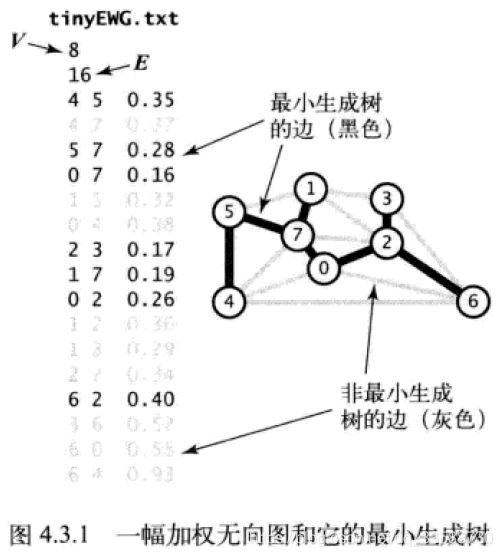
23.加权图指一种为每条边关联一个权值或是成本的图模型,例如在航空图中边表示航线,权值可以表示距离或者费用,在电路图中边表示导线,权值表示导线的长度即成本,或者信号通过导线的时间。这些应用场景下自然需要将成本最小化,加权无向图可以解决这些问题。图的生成树是它的一棵含有所有顶点的无环连通子图,一幅加权图的最小生成树(Minimum Spanning Tree,MST)是它的一棵权值(树中所有边的权值之和)最小的生成树,如下图所示:
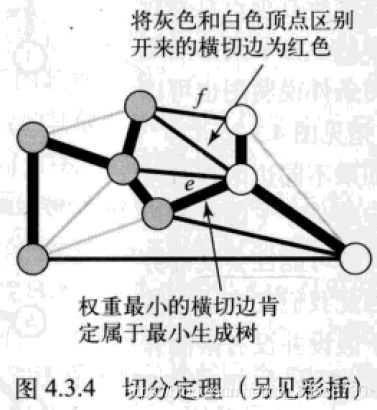
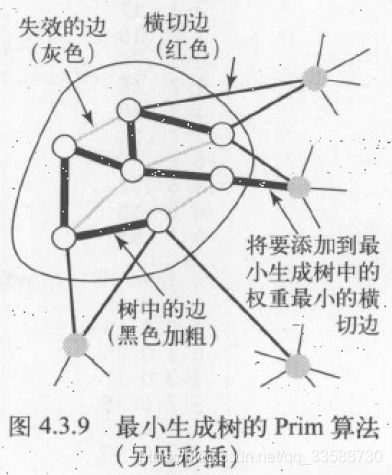
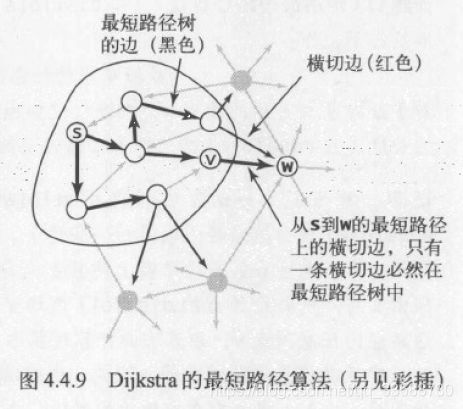
最小生成树只可能存在于连通图中。如果一幅图是非连通的,只能计算图中所有连通分量的最小生成树,多个连通分量自己的最小生成树形成最小生成森林。在最小生成树中,用一条边连接该树中的任意两个顶点都会产生一个环,从树中删去一条边会得到两棵独立的树。图的切分指将图的所有顶点分为非空且互不重叠的两个集合,横切边指将这两个集合连接起来的一条边,且图中权重最小的横切边必然属于最小生成树,如下图所示:
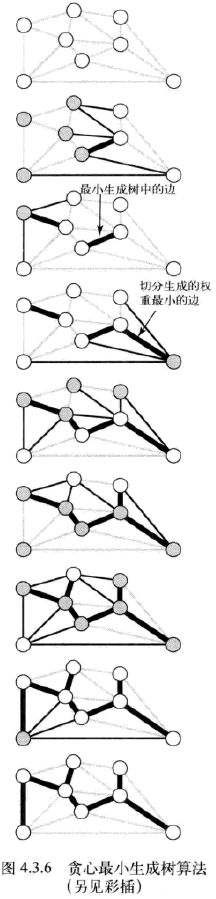
24.切分定理是解决最小生成树问题的所有算法的基础,这些算法都是一种贪心算法的特殊情况:使用切分定理找到最小生成树的一条边,不断重复直到找到最小生成树的所有边,实际操作为:为了将含有V个顶点的任意加权连通图中属于最小生成树的边标记为黑色,首先将所有边标为灰色,找到一种切分,它产生的横切边均不为黑色,在这些横切边中找到权重最小的横切边标记为黑色,重复直到标记V-1条黑色边为止,贪心算法的运行轨迹如下所示,每幅图都是一次切分,权重最小的横切边会黑色加粗并加入最小生成树中:
上述加权无向图数据结构的加权边代码实现如下所示:
package Chapter4_3Text;
public class Edge implements Comparable { //加权无向图中的加权边
private final int v; //一个结点
private final int w; //另一个结点
private final double weight; //边的权重
public Edge(int v,int w,double weight){
this.v=v;
this.w=w;
this.weight=weight;
}
public double weight(){return weight;} //返回边的权重
public int either(){return v;} //返回边两端的其中一个结点
public int other(int vertex){ //返回边两端的另一个结点
if(vertex==v) return w;
else if(vertex==w) return v;
else throw new RuntimeException("Iconsistent edge");
}
@Override
public int compareTo(Edge that) { //将这条边与that表示的另一条边比较权重
if(this.weight()that.weight()) return +1;
else return 0;
}
public String toString(){return String.format("%d-%d %.2f",v,w,weight);} //用字符串表示两条边的连接以及权重
}
以上面加权边代码为基础的加权无向图代码如下所示:
package Chapter4_3Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
public class EdgeWeightedGraph { //加权无向图
private final int V; //结点总数
private int E; //边的总数
private Bag[] adj; //和结点v相连的所有边的集合的数组
public EdgeWeightedGraph(int V){ //创建一副含有V个结点的空图,还没有边
this.V=V;
this.E=0;
adj=(Bag[]) new Bag[V];
for(int v=0;v();
}
//Exercise 4.3.9
public EdgeWeightedGraph(In in){ //从输入流中读取图文件并构造加权无向图
this(in.readInt()); //读取V并将图初始化
int E=in.readInt(); //读取E
for(int i=0;i adj(int v){return adj[v];} //返回结点v相连的所有边
public Iterable edges(){ //返回图的所有边
Bag b=new Bag();
for(int v=0;vv) b.add(e);
return b;
}
}
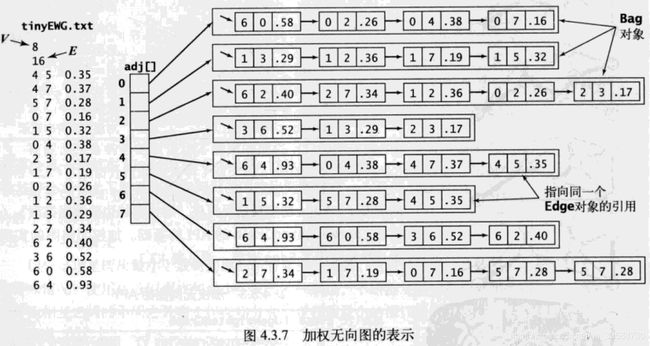
上述加权无向图代码中adj[]数组的示意图如下所示:
25.计算最小生成树的贪心算法中,其中一种是Prim算法,每一步都会为一棵生长中的树添加一条边,一开始这棵树只有1个结点,然后会向它添加V-1条边,每次总是将下一条连接树中顶点与不在树中的顶点且权重最小的边(黑色)加入树中,如下所示:
Prim算法的延时实现(即横切边失效了不会立刻从最小优先队列中被删除)的代码如下所示:
package Chapter4_3Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.MinPQ;
import edu.princeton.cs.algs4.Queue;
import edu.princeton.cs.algs4.StdOut;
public class LazyPrimMST { //产生最小生成树的Prim算法的延时实现
private boolean[] marked; //最小生成树中的结点,如果结点v在树中,marked[v]为true
private Queue mst; //最小生成树中的边
private MinPQ pq; //横切边的最小优先队列,包括已失效的横切边(即横切边另一端本不在树中的结点也已经加入到了树中)
private double weight; //最小生成树所有边的权重
public LazyPrimMST(EdgeWeightedGraph G){
pq=new MinPQ();
marked=new boolean[G.V()];
mst=new Queue();
visit(G,0); //为树添加一个结点,将它标记为已访问并将与它关联的所有未失效边加入优先队列,保证优先队列中含有所有连接树中结点与非树中结点的边,即横切边
while(!pq.isEmpty()){
Edge e=pq.delMin(); //从最小优先队列中得到权重最小的边
int v=e.either(),w=e.other(v); //获得一条边的两端结点
if(marked[v] && marked[w]) continue; //跳过已失效的横切边,即这条边两端的结点都已经在最小生成树中
mst.enqueue(e); //将这条权重最小的边加入到最小生成树中
weight+=e.weight(); //累加当前边的权重
if(!marked[v]) visit(G,v); //将结点v或w添加到最小生成树中
if(!marked[v]) visit(G,w);
}
}
private void visit(EdgeWeightedGraph G,int v){ //标记结点v(即放入最小生成树中)并将所有连接v和未标记结点的边(即横切边)加入最小优先队列pq
marked[v]=true;
for(Edge e:G.adj(v))
if(!marked[e.other(v)]) pq.insert(e);
}
public Iterable edges(){return mst;} //返回最小生成树的所有边
//Exercise 4.3.31
public double weight(){return weight;} //返回最小生成树的权重
public static void main(String[] args){
In in=new In(args[0]);
EdgeWeightedGraph G;
G=new EdgeWeightedGraph(in); //从输入流中构造加权无向图
LazyPrimMST mst=new LazyPrimMST(G); //通过构造函数产生最小生成树
for(Edge e:mst.edges()) //遍历输出最小生成树的所有边以及整个树的权重
StdOut.println(e);
StdOut.println(mst.weight());
}
}
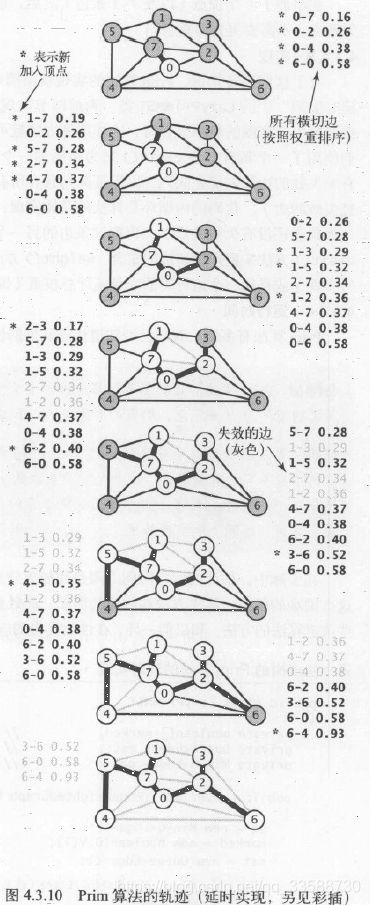
上述延迟实现的Prim算法的运行轨迹如下所示,该算法计算一幅含有V个顶点和E条边的连通加权无向图的MST所需的空间与E成正比,所需时间最坏情况下与ElogE成正比:
(1)将顶点0加入到MST中(visit()中的marked[0]=true),将该顶点的邻接链表(Bag的实际实现是链表)中的所有边添加到优先队列pq中(visit()中的pq.insert())。
(2)将顶点7和边0-7(因为这条边暂时权重最小)添加到MST中,将该顶点的邻接链表中的所有边添加到pq中。
(3)将顶点1和边1-7添加到MST中,将该顶点的邻接链表中所有边添加到pq中。
(4)将顶点2和边0-2添加到MST中,将边2-3和6-2添加到pq中,边2-7和1-2失效。
(5)将顶点3和边2-3添加到MST中,将边3-6添加到pq中,边1-3失效。
(6)将顶点5和边5-7添加到MST中,将边4-5添加到pq中,边1-5失效。
(7)从pq中删除失效的1-3、1-5和2-7(构造函数中的pq.delMin()和continue)。
(8)将顶点4和边4-5添加到MST中,将边6-4添加到pq中,边4-7和0-4失效。
(9)从pq中删除失效的边1-2、4-7和0-4。
(10)将顶点6和边6-2添加到MST中,和顶点6相关联的其他边都失效,此时图中已添加了V个顶点和V-1条边,最小生成树已完成,pq中余下的边都是无效的,不过不用再检查和删除。
26.上述Prim算法还有一种即时实现,即优先队列pq中的失效横切边会被及时删除。因为在最小生成树中,我们最关心的只是连接树中顶点与非树中顶点的权重最小的边,因此pq中只需要保存这条权重最小的那条边,在将结点v添加到树中后检查是否需要更新这条权重最小的边(因为v-w的权重可能更小),所以pq中保存的是每个非树中顶点w的一条权重最小的横切边(与树中顶点连接的边)。Prim算法的即时实现代码如下所示:
package Chapter4_3Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.IndexMinPQ;
import edu.princeton.cs.algs4.StdOut;
public class PrimMST { //产生最小生成树的Prim算法的即时实现,即横切边失效后将被立刻删除,只保存每个非树中结点连接树中结点的权重最小横切边
private Edge[] edgeTo; //非树中结点v和树中结点连接的最小权重横切边,最终会作为MST中的边
private boolean[] marked; //如果结点v在树中则为true
private double[] distTo; //非树中结点v和树中结点连接的最小权重横切边的权重,distTo[w]=edgeTo[w].weight(),最终会作为MST中的边权重
private IndexMinPQ pq; //索引最小优先队列,保存非树中结点v连接树中结点的未失效最小权重横切边的权重,该结点v会是下一个将被添加到树中的结点,v对应的最小权重边会作为MST中的边
public PrimMST(EdgeWeightedGraph G){
edgeTo=new Edge[G.V()];
distTo=new double[G.V()];
marked=new boolean[G.V()];
for(int v=0;v(G.V());
distTo[0]=0.0;
pq.insert(0,0.0); //用结点0和权重0初始化pq,树中第1个结点连接自己的权重当然是0
while(!pq.isEmpty()) //将最小权重横切边另一端的非树中结点加入到最小生成树中
visit(G,pq.delMin());
}
private void visit(EdgeWeightedGraph G,int v){ //将结点v添加到树中,更新权重和横切边等数据
marked[v]=true;
for(Edge e:G.adj(v)){
int w=e.other(v); //w是刚加入树中的原非树中结点v连接的另一端结点
if(marked[w]) continue; //如果结点w和结点v一样都已经在树中,则横切边v-w失效跳过这一轮循环,失效的横切边不会被加入edgeTo[]数组
if(e.weight() edges(){ //遍历最小生成树中的所有边
Bag mst=new Bag();
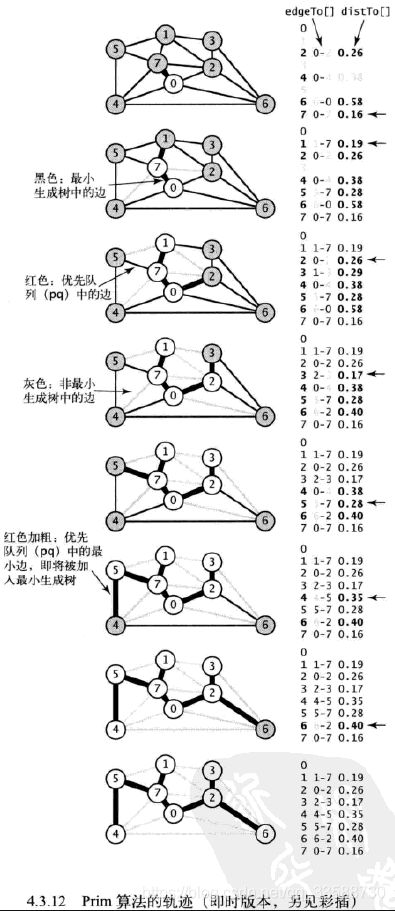
for(int v=1;v 上述代码的运行轨迹如下所示,Prim算法的即时版本所需时间和ElogV成正比,空间和V成正比。对实际应用中经常出现的巨型稀疏图,延时实现和即时实现在时间上限上没什么区别,但空间上限中即时实现的算法更少,变成了延时实现的一个常数因子。树的生长都是通过连接一个和新加入树的结点相邻的结点,当新加入的顶点周围没有非树中顶点时,树的生长又会从另一部分开始:
(1)将顶点0加入最小生成树中,将它的邻接链表(Bag对象)中的所有边添加到优先队列pq之中,因为这些边都是目前唯一已知的连接非树中顶点与树中顶点的最短边(distTo[]都大于Double.POSITIVE_INFINITY)。
(2)将顶点7和边0-7加入到MST(marked[7]=true和edgeTo[7])中,将边1-7和5-7添加到pq中,将连接顶点4与树的最小权重边由0-4换为4-7,2-7不会影响到pq,因为它的权重(distTo[2])大于0-2的权重。
(3)将顶点1和边1-7添加到MST中,将边1-3添加到pq中(5-7的权重distTo[5]比1-5的权重小,所以不加入1-5)。
(4)将顶点2和边0-2加入到MST中,将连接顶点6与树的最小边由0-6替换为6-2,将连接顶点3与树的最小边由1-3替换为2-3。
(5)将顶点3和边2-3加入到MST中。
(6)将顶点5和边5-7添加到MST中,将连接顶点4与树的最小权重边由4-7替换为4-5。
(7)将顶点4和边4-5添加到MST中。
(8)将顶点6和边6-2添加到MST中。此时MST中已添加V-1条边,MST完成且pq为空。
27.除了上述Prim算法,还有一种Kruskal算法可以用于产生最小生成树,主要思想是按照边的权重顺序(从小到大)处理它们,将边加入MST中,加入的边不会与已经加入的边构成环,直到树中有V-1条边为止。Kruskal算法虽然与Prim一样也是一条边一条边地构造MST,但不同的是它一开始将一张图看成V个单结点森林,然后寻找最小权重边将两个森林合并为一个,最终只剩下一个大森林,即为MST。Kruskal算法的代码实现如下所示:
package Chapter4_3Text;
import edu.princeton.cs.algs4.*;
public class KruskalMST { //产生最小生成树的Kruskal算法
private Queue mst; //保存MST中的所有边
private double weight; //边的权重
public KruskalMST(EdgeWeightedGraph G){
mst=new Queue();
MinPQ pq=new MinPQ(); //使用最小优先队列将所有边按照权重排序
for(Edge e:G.edges()) pq.insert(e); //将图中的所有边插入到最小优先队列中
UF uf=new UF(G.V()); //使用1.5节中的union-find数据结构识别会形成环的边
while(!pq.isEmpty() && mst.size() edges(){return mst;} //返回最小生成树的所有边
//Exercise 4.3.31
public double weight(){return weight;} //返回最小生成树的边权重和
public static void main(String[] args){
In in=new In(args[0]);
EdgeWeightedGraph G;
G=new EdgeWeightedGraph(in); //从输入流中构造加权无向图
LazyPrimMST mst=new LazyPrimMST(G); //通过构造函数产生最小生成树
for(Edge e:mst.edges()) //遍历输出最小生成树的所有边以及整个树的权重
StdOut.println(e);
StdOut.println(mst.weight());
}
}
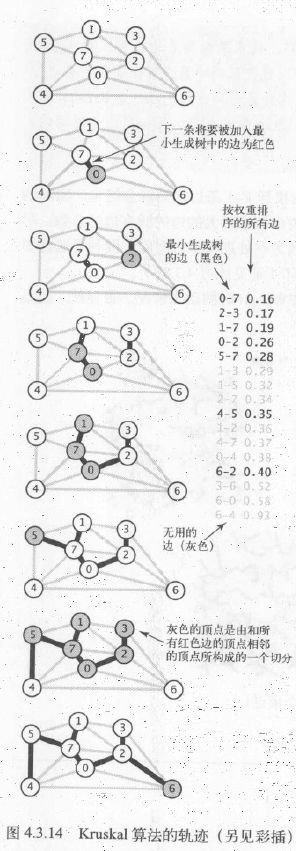
上述代码的运行轨迹和结果如下所示,Kruskal算法计算一幅含有V个顶点和E条边的连通加权无向图的最小生成树所需空间和E成正比,所需时间和ElogE成正比(最坏情况),Kruskal算法一般比Prim算法慢,因为处理每条边时除了两种算法都要完成的优先队列操作以外,它还需要进行一次connect()操作:
28.各种最小生成树算法的性能特点如下所示,在大部分应用场景中,都可以使用上面所学的算法在线性时间内得到图的MST,只是对于一些稀疏图所需的时间要乘以logV:
四、最短路径、最长路径、任务调度等动态规划
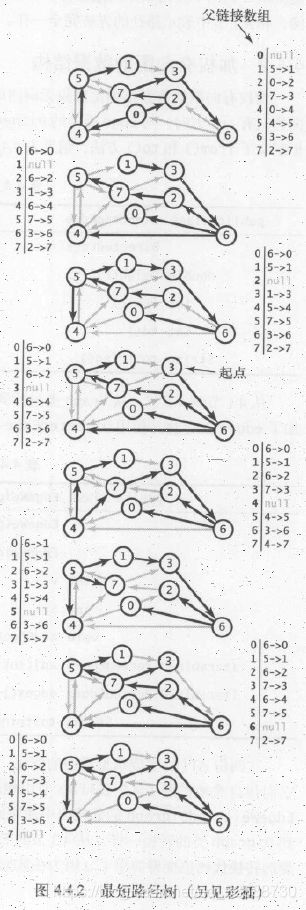
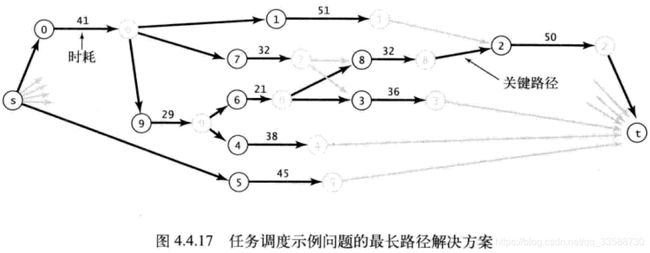
29.针对最短路径的处理,大部分情况下都会使用加权有向图,每条有向路径都有一个与之关联的路径权重,等于路径中每条有向边的权重之和,这样最短路径问题就变成“找到从一个顶点到达另一个顶点的权重最小的有向路径”。权重不一定是距离,也可以是时间、花费和其他不一定与距离成正比的东西。其中,设一个起点是s,那么从s到所有可达顶点的最短路径构成了一棵最短路径树(SPT),它是图的一幅子图,包含s和s可达的所有结点,这棵有向树的根节点为s,树的每条路径都是有向图中的一条最短路径。以不同顶点为起点所生成的最短路径树的示意图如下所示。
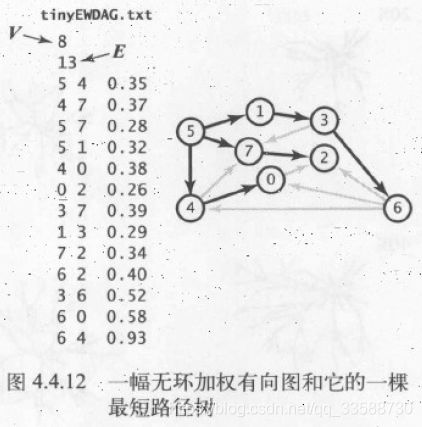
加权有向边的数据结构表示比无向边更简单,如下面代码所示:
package Chapter4_4Text;
public class DirectedEdge { //加权有向边的数据结构
private final int v; //边的起点
private final int w; //边的终点
private final double weight; //边的权重
public DirectedEdge(int v,int w,double weight){
this.v=v;
this.w=w;
this.weight=weight;
}
public double weight(){return weight;} //返回加权有向边的权重
public int from(){return v;} //返回这条边的起点
public int to(){return w;} //返回这条边指向的顶点
public String toString(){return String.format("%d->%d %.2f",v,w,weight);} //按照格式输出
}
在上面加权有向边实现的基础上,加权有向图的数据结构实现如下所示:
package Chapter4_4Text;
import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
public class EdgeWeightedDigraph { //加权有向图
private final int V; //顶点总数
private int E; //边的总数
private Bag[] adj; //和结点v相连的所有边的集合的数组,即如果一条边从v指向w,那么它只会出现在v的邻接链表adj[v]中
public EdgeWeightedDigraph(int V){ //创建一副含有V个结点的空图,还没有边
this.V=V;
this.E=0;
adj=(Bag[]) new Bag[V];
for(int v=0;v(); //结点v可能连接多条有向边,所以用Bag数组表示
}
public EdgeWeightedDigraph(In in){ //从输入流中读取图文件并构造加权有向图
this(in.readInt()); //读取V并将图初始化
int E=in.readInt(); //读取E
if(E<0){
throw new IllegalArgumentException("The weight of edges must be nonnegative.");
}
for(int i=0;i adj(int v){return adj[v];} //返回所有从结点v指出去的边
public Iterable edges(){
Bag bag=new Bag();
for(int v=0;v 上述加权有向图代码的图示如下所示,在构造过程中边被按照顺序一条条加入图中,如果一条边从v指向w,那么它只会出现在v的邻接链表中(adj[v]),且每条边只会出现一次:
30.以上面加权有向边和加权有向图的实现为基础,利用Dijkstra算法构造最短路径树并查找最短路径(前提条件是图中所有边的权重非负)的代码实现如下所示:
package Chapter4_4Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.IndexMinPQ;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;
public class DijkstraSP { //最短路径的Dijkstra算法
private DirectedEdge[] edgeTo; //最短路径树中连接结点v和它的父节点的边,即edgeTo[v]是从起点s到v的最短路径上的最后一条边
private double[] distTo; //从起点s到v的最短路径长度,如果不存在则路径距离为无穷大
private IndexMinPQ pq; //索引最小优先队列,保存需要被relax()方法放松的结点并确认下一个被放松的结点
public DijkstraSP(EdgeWeightedDigraph G,int s){
edgeTo=new DirectedEdge[G.V()];
distTo=new double[G.V()];
pq=new IndexMinPQ(G.V());
for(int v=0;vdistTo[v]+e.weight()){ //如果从s到w的距离大于从s到v的距离加上v到w的距离之和,则更新更短路径,如果这个和的值不小于distTo[w],则边e失效并被忽略,跳过一轮循环
distTo[w]=distTo[v]+e.weight();
edgeTo[w]=e;
if(pq.contains(w)) pq.change(w,distTo[w]); //如果优先队列中有结点w的信息,则更新从起点s到达w的距离,否则插入关于w的新条目,w会成为接下来被relax()方法放松的结点
else pq.insert(w,distTo[w]);
}
}
}
public double distTo(int v){return distTo[v];} //返回从起点通往结点v的路径距离
public boolean hasPathTo(int v){return distTo[v] pathTo(int v){ //从起点s到结点v的路径,如果不存在则为null
if(!hasPathTo(v)) return null;
Stack path=new Stack();
for(DirectedEdge e=edgeTo[v];e!=null;e=edgeTo[e.from()]) //从指向结点v的那条边开始,不断回退到指向父结点的边,最终回退到起点s指出的有向边
path.push(e); //将不断回退的有向边加入栈中,这样栈中路径按照相反顺序弹出后,就是正序的从起点s到结点v的路径
return path;
}
public static void main(String[] args){
EdgeWeightedDigraph G=new EdgeWeightedDigraph(new In(args[0])); //接受一个输入流和一个起点作为命令行参数
int s=Integer.parseInt(args[1]);
DijkstraSP sp=new DijkstraSP(G,s); //从输入流中读取有向图,根据起点计算有向图的最短路径树
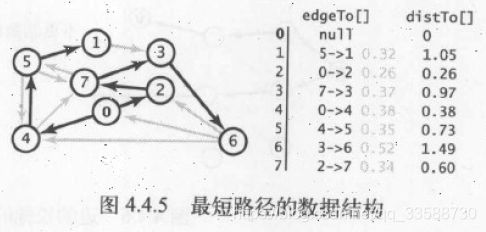
for(int t=0;t 其中最短路径的数据结构,edgeTo[]和distTo[]的示意图如下所示:
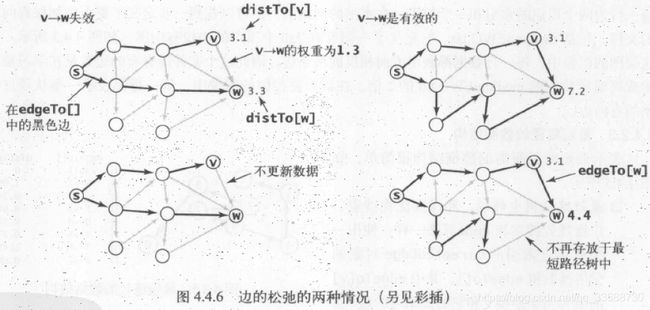
relax()方法的边松弛有两种情况,即从起点s到结点v再到w的距离大于从起点s到w的距离(v->w失效),与从起点s到结点v再到w的距离小于从起点s到w的距离(v->w有效),如下所示:
pathTo()方法的计算轨迹如下所示:
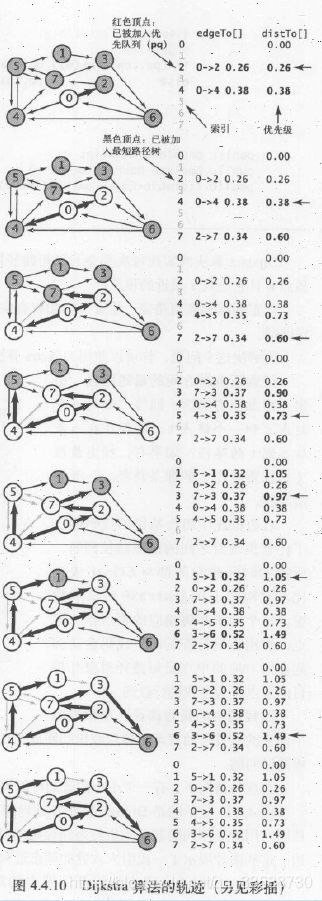
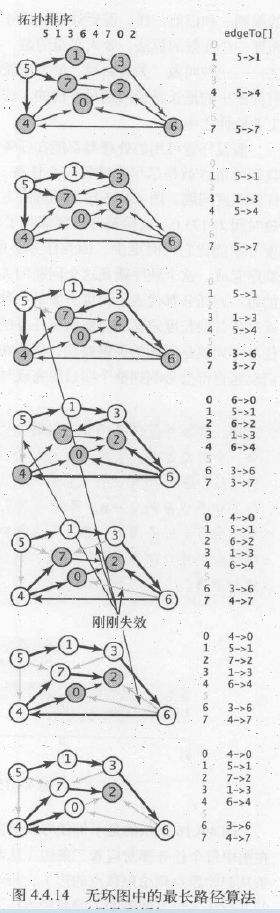
上述Dijkstra算法代码构造最短路径树,并找到从起点0到结点6的最短路径的过程如下(按照从起点到某结点的路径距离总权重来排序,从优先队列中先取出总权重最小的):
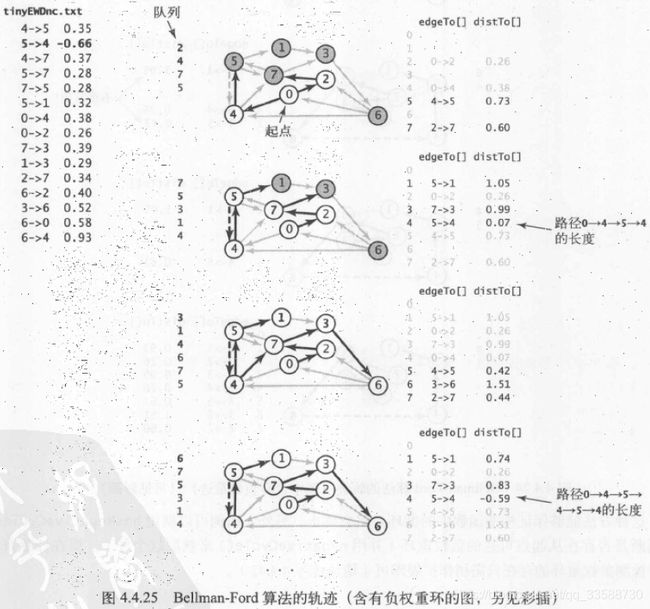
(1)将顶点0添加到最短路径树sp中,将顶点2和4加入优先队列pq。
(2) 在relax()中将0→2添加到树中,从构造函数里将pq中删除顶点2,将顶点7加入pq。
(3) 将0→4添加到树中,从pq中删除顶点4,将顶点5加入pq,边4→7失效(因为0→2→7的距离比0→4→7的距离短)。
(4) 将2→7添加到树中,从pq中删除顶点7,将顶点3加入pq,边7→5失效(因为0→4→5的距离比0→2→7→5的距离短)。
(5)将4→5添加到树中,从pq中删除顶点5,将顶点1加入pq,边5→7失效(因为0→2→7的距离比0→4→5→7的距离短)。
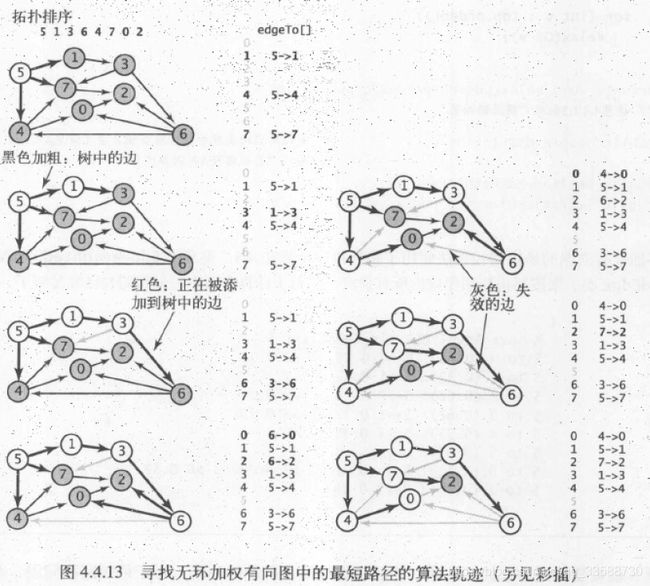
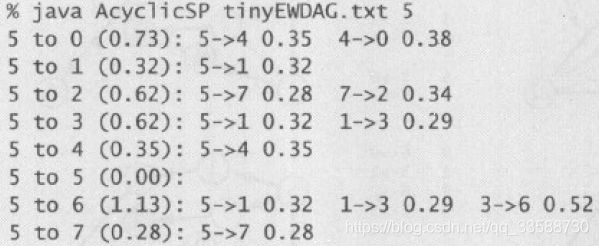
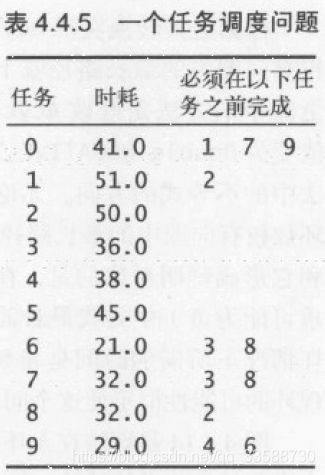
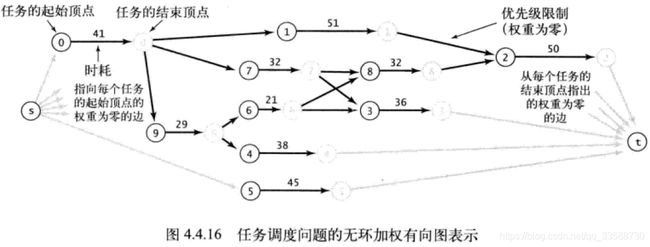
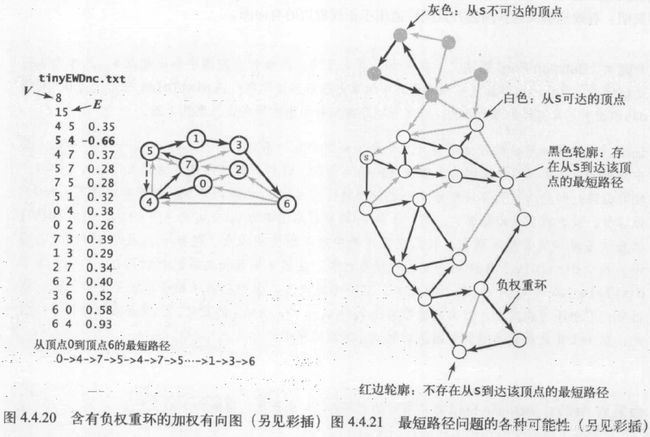
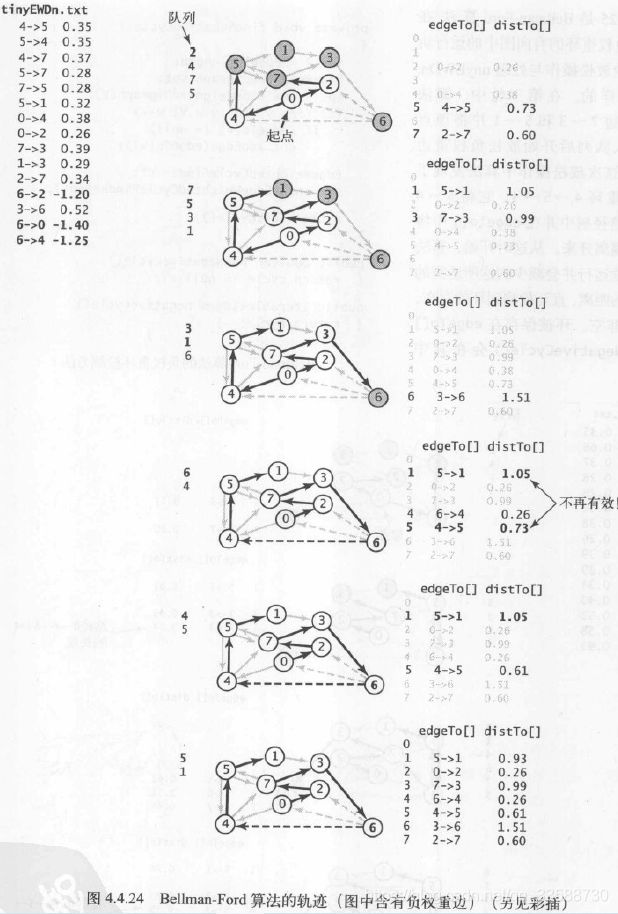
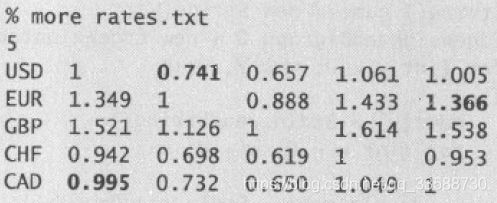
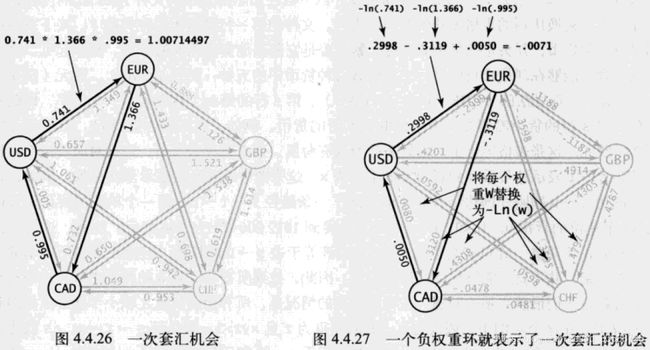
(6)将7→3添加到树中,从pq中删除顶点3(distTo[5] (7)将5→1添加到树中,从pq中删除顶点1,边1→3失效(因为0→2→7→3的距离比0→4→5→1→3的距离短)。 (8)将3→6添加到树中,从pq中删除顶点6,最短路径查找完成。 在一幅含有V个顶点和E条边的加权有向图中,使用Dijkstra算法计算根节点为起点的最短路径树所需的空间与V成正比,时间与ElogV成正比(最坏情况)。上述代码运行的结果如下所示: 31.利用上面DijkstraSP算法计算任意某两个结点之间的最短路径的代码如下所示: 32.在无环加权有向图中计算最短路径,需要用到拓扑排序和环检测的逻辑,在无环加权有向图中环检测代码的实现如下所示: 以环检测代码为基础,在无环加权有向图中对结点进行拓扑排序的代码如下所示: 以上述环检测和结点拓扑排序的代码为基础,对结点进行逆后序拓扑排列后,在无环加权有向图中利用拓扑排序的最短路径算法实现如下所示: 上述计算最短路径的代码的运行轨迹如下所示,按照拓扑排序的顺序放松结点,能够在E+V成正比的时间内解决无环加权有向图的单点最短路径问题,在已知加权图是无环的情况下,该算法已经是找出最短路径的最好方法: (1)用深度优先搜索(DFS)得到图的顶点拓扑排序5,1,3,6,4,7,0,2(逆后序)。 (2)将顶点5和从它指出的所有边添加到最短路径树中。 (3)将顶点1和边1→3添加到树中。 (4)将顶点3和边3→6添加到树中,边3→7已经失效(因为5→7的距离权重小于5→1→3→7)。 (5)将顶点6和边6→2、6→0添加到树中,边6→4已经失效(因为起点5可以直接到达4,距离权重更小)。 (6)将顶点4和边4→0添加到树中,边4→7和6→0已经失效(因为5→7的权重小于5→4→7,5→4→0的权重小于5→1→3→6→0)。 (7)将顶点7和边7->2添加到树中,边6→2已经失效(因为5→7→2的权重小于5→1→3→6→2)。 (8)将顶点0添加到树中,边0→2已经失效(因为5→7→2的权重小于5→4→0→2)。 (9)将顶点2添加到树中,从起点5开始构造最短路径树完成。 上面的代码实现中没有用到marked[]数组,因为按照拓扑顺序处理DAG中的顶点,所以不可能再次遇到已经被放松过的顶点。上面代码的运行结果如下所示: 33.除了查找最短路径,还可以在无环加权有向图中寻找最长路径,其中边的权重可正可负,只需要修改上面AcyclicSP代码,将distTo[]的初始值变为Double.NEGATIVE_INFINITY并改变relax()方法中不等式的方向即可。在之前DepthFirstOrder和Topological实现中,基础思想是单线程的任务优先级处理,一个任务处理好才能进行下一个任务的拓扑排序,完成任务的总耗时就是所有任务所需要的总时间。但是如果有这样的场景,即多任务并行处理,并行度不限,给定一组任务及每个任务所需时间,以及一组关于任务完成先后次序的优先级限制,如何在满足次序限制条件的前提下,多线程并行安排任务并在最短的时间内完成所有任务? 针对该问题,正好有一种线性时间的称为“关键路径”的算法能够证明该问题与无环加权有向图中的最长路径问题是等价的。在无环加权有向图中寻找最长路径的代码如下所示: 上述计算最长路径代码在图文件tinyEWDAG.txt中的运行轨迹如下所示: (1)用深度优先搜索得到图顶点的拓扑排序5、1、3、6、4、7、0、2,将顶点5和从它指出的所有边添加到最长路径树中。 (2)将顶点1和边1→3添加到树中。 (3)将顶点3和边3→6、3→7添加到树中,边5→7已经失效(因为它的权重比5→1→3→7小)。 (4)将顶点6和边6→2、6→4和6→0添加到树中。 (5)将顶点4和边4→0、4→7添加到树中,边6→0和3→7已经失效(因为6→0的权重小于6→4→0,3→7的权重小于3→6→4→7)。 (6)将顶点7和边7→2添加到树中,边6→2已经失效(因为它的权重小于6→4→7→2)。 (7)将顶点0添加到树中,边0→2已经失效(因为它的权重小于7→2)。 (8)将顶点2添加到树中,以结点5为起点的最长路径树构造完成。 以上述计算最长路径的代码实现为基础,多线程并行执行任务时,关键路径即任务安排树中某条最长路径,该路径的花费时间就是所有任务的完成时间,例如下面任务调度的例子: 由该限制条件可知,这些任务必须按照0→9→6→8→2的顺序完成,所以这个顺序就是该例子的关键路径,该路径的时间最长,成为所有任务完成的总时间,如下所示: 根据该任务调度的关键路径图,可以得到该任务调度问题的无环加权有向图表示,为了方便代码实现,所有顶点自身都包括一个同名的起始顶点和结束顶点,并在有向加权无环图的左侧加上所有起始顶点的起点s,以及在图的右侧加上所有结束顶点的终点t,s指向所有顶点的起始顶点,所有顶点的结束顶点指向t,其中自己的起始顶点指向自己的结束顶点的边表示完成该任务所花的时间权重,每个顶点指向除自己以外的顶点时,这条边的权重为0,如下所示: 根据上面的描述,图中每个任务都对应三条边,即起点s到起始顶点(权重为0)、自身的起始顶点到结束顶点(任务权重)、结束顶点到终点s(权重为0)。在优先级限制下的并行任务调度问题,转化为在无环加权有向图中的最长路径问题的代码实现如下所示: 上述代码的执行结果如下所示,解决优先级限制下并行任务调度问题的关键路径算法所需时间为线性级别: 34.之前的算法基本都针对无环图,且边的权重非负,在有优先级限制条件、还包括相对最后期限限制的并行任务调度场景下并不适用,例如某个任务必须在指定的时间点之前开始,如任务v必须在任务w开始后的d个单位时间内也开始,此时在有向图中,可以添加一条从v指向w的权重为-d的负权重边来表示,此时这种有相对最后期限限制的并行任务调度问题,实际上可以转化为加权有向图中可能存在环和负权重边的最短路径问题。这种有环和负权重的加权有向图如下所示: 在某些包含负权重边的加权有向图中,可能还包含负权重环,即有向环上每条边的权重之和为负值,不需要每条边都是负权重。但是如果从s到某个顶点v的路径上,中间某个顶点在这样的一个负权重环上,那么从s到v的最短路径是不存在的,包含负权重环的最短路径问题没有意义,因为有向环可以不断转圈循环计算成任意无穷小的负权重和,如下所示: 因此,只有加权有向图中从s到v的有向路径存在且路径上任意顶点都不在任何负权重环上时,s到v的最短路径才是存在的。根据这种思路,可以使用Bellman-Ford算法解决这个问题(之前的算法都只针对非负权重边),即以任意顺序放松含有V个顶点的有向图的所有边,重复V轮,代码如下所示: Bellman-Ford算法解决可能含负权重环的加权有向图中的最短路径问题,最坏情况下所需的时间和EV成正比,空间和V成正比。在含有负权重边的图中运行轨迹如下所示: (1)将起点加入队列queue,放松边0→2和0→4并将顶点2、4加入queue。 (2)放松边2→7并将顶点7加入queue,放松边4→5并将顶点5加入queue,然后放松失效的边4→7(因为0→2→7的权重小于0→4→7)。 (3)放松边7→3和5→1,并将顶点3和1加入queue,放松失效的边5→4和5→7(因为0→4权重小于0→4→5→4,0→2→4权重小于0→4→5→7)。 (4)放松边3→6并将顶点6加入queue,放松失效的边1→3(因为0→2→7→3权重小于0→4→5→1→3)。 (5)放松边6→4并将顶点4加入queue,该边为负权重边路径更短,所以要再次放松顶点4指出的边。从起点0到顶点5和1的距离权重已经失效将在下一轮中修正(0经过6到4的权重小于0→4的权重)。 (6)放松边4→5并将顶点5加入queue,放松失效的边4→7(0→2→7的权重小于0经过6到4再到7的权重)。 (7)放松边5→1并将顶点1加入queue,放松失效的边5→4和5→7。 (8) 放松失效的边1→3,queue为空结束。 由上可知,队列每排空一次为一轮(在当前几个队列中结点被排出,并插入它们指向的结点之前),因此8个结点放松操作重复了8轮。下面的例子图结构相同,但是含有负权重环,则前两轮的步骤相同,第(3)轮中将顶点3和1加入queue后,放松负权重边5→4会出现负权重环4→5→4,5→4会被加入到edgeTo[]中,然后relax()会不断在这个环中循环,此时该环与起点0在edgeTo[]中被隔开了(0→4权重大于5→4),算法会一直在环中运行直到达到检测环方法的触发条件,如下所示: 35.用到上述Bellman-Ford算法的一个典型实际例子就是检测金融货币中的套汇操作。例如下面的文件,第一行是火笔的种类数V,接下来每一行都对应一种货币,以及相对于各货币的汇率,即用t货币购买一个单位的第s行货币,需要多少个单位的第t行的货币: 这样的表格相当于一副加权有向图,顶点为货币,有向边权重为汇率。如果有一条路径s→t→u,则一个单位的货币s可以兑换到xy个单位的货币u,但经过了中间货币t兑换的汇率之积xy,未必与s直接兑换u的汇率相同,于是某些投机者会关心汇率之积比直接兑换汇率更大的环路径s→t→u→s,将原货币经过几次中间货币兑换,再兑换回原货币,反而赚钱了。 这种环路径的套汇操作,实际上等价于加权有向图中的负权重环检测问题,权重积w1w2….wn可以对应通过自然对数取反的和-ln(w1)- -ln(w2)-…-ln(wn),成为图中的实际权重weight,在计算能兑换多少其他货币时再乘以e^(-weight)。因为对数函数是单调的,且已经取反,所以当边的负权重之和最小时,汇率之积正好最大,因此每一个负权重环都是一个套汇的机会,如下所示: 利用负权重环检测,货币兑换中的套汇代码如下所示: 该算法的执行结果如下所示: 36.几种最短路径算法实现的比较如下所示: package Chapter4_4Text;
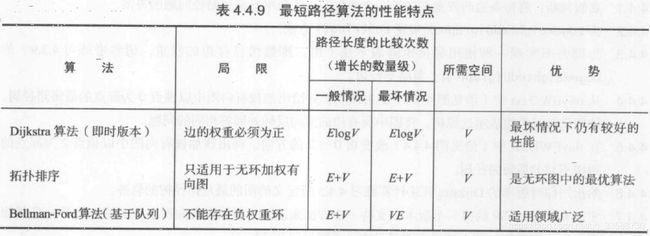
public class DijkstraAllPairsSP { //任意结点对之间的最短路径,给定起点s与终点t,找到从s到t的最短路径
private DijkstraSP[] all; //构造DijkstraSP对象数组,每个元素都把索引对应的结点作为起点
DijkstraAllPairsSP(EdgeWeightedDigraph G){
all=new DijkstraSP[G.V()];
for(int v=0;vpackage Chapter4_4Text;
import edu.princeton.cs.algs4.Stack;
//Exercise 4.4.12
public class EdgeWeightedCycleFinder { //在有向图中利用DFS寻找有向环
private boolean[] marked; //用于标记结点是否由起点s可达,如果从起点s可以到达结点v,经过结点v就会使marked[v]置为true,没经过的结点w会使marked[w]为false
private DirectedEdge[] edgeTo; //最短路径树中连接结点v和它的父节点的边,即edgeTo[v]是从起点s到v的最短路径上的最后一条边
private Stackpackage Chapter4_4Text;
//Exercise 4.4.12
public class EdgeWeightedTopological { //结点的拓扑排序
private Iterablepackage Chapter4_4Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;
public class AcyclicSP { //无环加权有向图中利用拓扑排序的的最短路径算法,比Dijkstra算法更快、更简单
private DirectedEdge[] edgeTo; //最短路径树中连接结点v和它的父节点的边,即edgeTo[v]是从起点s到v的最短路径上的最后一条边
private double[] distTo; //从起点s到v的最短路径长度,如果不存在则路径距离为无穷大
public AcyclicSP(EdgeWeightedDigraph G,int s){
edgeTo=new DirectedEdge[G.V()];
distTo=new double[G.V()];
for(int v=0;vpackage Chapter4_4Text;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
//Exercise 4.4.28
public class AcyclicLP { //有向无环图中的最长路径
private DirectedEdge[] edgeTo; //最长路径树中连接结点v和它的父节点的边,即edgeTo[v]是从起点s到v的最长路径上的最后一条边
private double[] distTo; //从起点s到v的最长路径长度,如果不存在则路径距离为负无穷大
public AcyclicLP(EdgeWeightedDigraph G,int s){
edgeTo=new DirectedEdge[G.V()];
distTo=new double[G.V()];
for(int v=0;vpackage Chapter4_4Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class CPM { //优先级限制下的并行任务调度问题,通过有向加权无环图中的最长路径计算来找到关键路径
public static void main(String[] args){
int N= StdIn.readInt(); //读取结点数
StdIn.readLine();
EdgeWeightedDigraph G=new EdgeWeightedDigraph(2*N+2); //因为每个结点都会分解为一个起始节点和结束结点,所以数量乘以2,再加上一个起点s和一个终点t
int s=2*N,t=2*N+1; //结点索引是从0开始的,所以倒数2个结点是2N和2N+1,分别作为起点和终点的索引
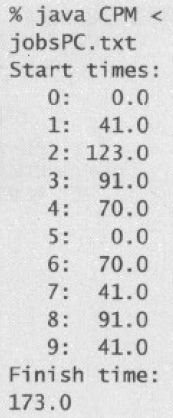
for(int i=0;ipackage Chapter4_4Text;
import edu.princeton.cs.algs4.Queue;
import edu.princeton.cs.algs4.Stack;
public class BellmanFordSP { //基于队列的Bellman-Ford算法,解决不存在负权重环的加权有向图中的最短路径问题,可以存在负权重边
private double[] distTo; //从起点到某个结点的路径长度,如果该结点不可达则路径距离为+∞,如果该结点可达但在负权重环中,则路径距离为-∞
private DirectedEdge[] edgeTo; //从起点到某个结点的最后一条边
private boolean[] onQ; //对应索引的结点是否已经存在于队列中
private Queuepackage Chapter4_4Text;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class Arbitrage { //利用负权重环检测进行货币兑换的套汇
public static void main(String[] args){
int V= StdIn.readInt(); //读取货币种类数
String[] name=new String[V]; //存放每种货币名称
EdgeWeightedDigraph G=new EdgeWeightedDigraph(V); //创建一副含有V个结点的空图,还没有边
for(int v=0;v