算法分析与设计第三周练习（图论）

目录

Evaluate Division

Reconstruct Itinerary

总结

---

Evaluate Division

1. 题目

Equations are given in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating point number). Given some queries, return the answers. If the answer does not exist, return -1.0.

Example:
Given a / b = 2.0, b / c = 3.0. 
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? . 
return [6.0, 0.5, -1.0, 1.0, -1.0 ].

The input is: vector> equations, vector& values, vector> queries , where equations.size() == values.size(), and the values are positive. This represents the equations. Return vector.

According to the example above:

equations = [ ["a", "b"], ["b", "c"] ],
values = [2.0, 3.0],
queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ]. 

 

The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction.

2. 分析

2.1 基础知识

图论的内容是算法中比较重要并且难度比较大的一部分内容，在课本的第三章都是与图论有关的内容，并且这一整章的内容都是以DFS算法为基础的，图基于DFS算法的应用有（基于课本）：

     1. 简单的DFS算法。

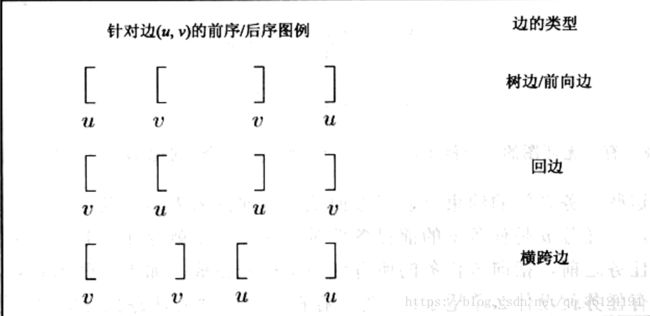
     2. 判断图树边，前向边，回边。

        

        通过在遍历前和遍历后的时钟进行计时，通过时钟的计时可以判断出具体的边，具体的规则如下：

        

     3. 通过边的类型判断图是否有环，如果通过DFS发现有回边，则图有环。其实这里还可以通过节点的入度判断图是否有环，             具体是从源点开始遍历，遍历完了有这个点有边的节点入度减1，最后如果有节点入度不等于0，则图有环。

    4. 拓扑排序，可以通过时钟计时的方式找出拓扑排序。

    5. 最后一个是图的连通性，强连通性等等。

2.2 解体思路

我们需要对这题的元素进行一些抽象，这题给定了一些预定义的公式，然后通过预定义公式的演化求出目的公式的值，这样看起来是比较具体的，然后我们抽象出来一个模型，这个模型就是图。

由于公式之间的运算只有一种运算，所以我们可以将预定义两个字符得运算看成是构成图的边，并且这个边是双向的，但权值不一样，按照预定义的公式，我们得出了一个图，但图有两种表述方式，一种是邻接矩阵，一种是邻接链表，明显，邻接链表是最常用的，我们这里采用邻接链表，但需要做一些变形，因为这样有权值和string类型需要表达进数据结构当中，其数据结构是：

map>> graph;

由于我们需要存某个点相邻的点及其权值，这样可以有利于搜索。

图建立好以后，我们需要求任何两个点的计算的值，也就是说，我们需要找出这两个节点的路径，寻找的办法是DFS，同时还需要距离路径的权值，抽象为图论问题去解决就是搜索某条路径及其权值，而权值恰好就是两个string相除的值。

3. 源码

class Solution {
public:
	double dfs(string source, string dest, set &visited, map>> &graph) {
		if(source == dest) {
			return 1.0;
		}
		visited.insert(source);
		for(int i = 0; i < graph[source].size(); i++) {
			if(visited.find(graph[source][i].first) == visited.end()) {
				double num = dfs(graph[source][i].first, dest, visited, graph);
				if(num != -1.0) {
					return (num*graph[source][i].second);
				}
			}
		}
		return -1.0;
	}

    vector calcEquation(vector> equations, vector& values, vector> queries) {
        map>> graph;
        for(int i = 0; i < equations.size(); i++) {
        	graph[equations[i].first].push_back(make_pair(equations[i].second, values[i]));
        	graph[equations[i].second].push_back(make_pair(equations[i].first, 1/values[i]));
        }
        
       /* for(auto a : graph) {
        	cout << a.first << endl;
        }
        */
        vector result;
        for(int i = 0; i < queries.size(); i++) {
        	if(graph.find(queries[i].first) == graph.end()) {
        		result.push_back(-1.0);
        		continue;
        	}
        	set visited;
        	string source = queries[i].first;
        	string dest = queries[i].second;
        	double num = dfs(source, dest, visited, graph);
        	result.push_back(num);
        }
        return result;
    }
};

Reconstruct Itinerary

1. 题目

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

1. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
2. All airports are represented by three capital letters (IATA code).
3. You may assume all tickets form at least one valid itinerary.

Example 1:

Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

Example 2:

Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
             But it is larger in lexical order.

2. 分析

这题可以看作是DFS的变形，首先，这里重建路径的过程可以看作是有向图的遍历过程，但这与图的遍历有些不同，因为两个地方之间是可以往返的，也就是说，一个定点有可能遍历两次，如下的一个测试样例充分说明了问题

JFK这个定点被遍历了三次，在c++当中，如果图的定点是string或者char类型，用map这个数据结构表达起来是非常方便的，但这里由于可以往返，意味这一个顶点可以有两条边指向同一个顶点，所以我们选择用multiset存顶点指向的边（本来是用set的，但提交后发现有上面图示的特殊情况，所以改成multiset）。还有一个要注意的是遍历的顺序，set刚好是自动有序的，所以不需要我们额外排序，当遍历的顺序是降序，所以最后我们需要把结果回溯一下。

3. 源码

class Solution {
public:
	void DFS(string source, map > &graph, vector &result) {
		while(graph[source].size()) {
			string temp = *graph[source].begin();
			graph[source].erase(graph[source].begin());
			DFS(temp, graph, result);
		}
		result.push_back(source);
	}

    vector findItinerary(vector> tickets) {
        map > graph;
        vector result;
        for(auto a : tickets) {
        	graph[a.first].insert(a.second);
        }
        string start = "JFK";
        DFS(start, graph, result);
        vector r(result.rbegin(), result.rend());
        return r;
    }
};

总结

做了几道与图相关的图后，发现一个有趣的规律，本来我们说图得表达方式有两种，一种是邻接矩阵，一种是邻接链表。但这里我们没有用到这两种。而是用map和vector对其进行代替，但我们从本质上看，其实map和vector结合的方式对矩阵进行表达实质是邻接矩阵的变形，其实与邻接矩阵没有太大的区别。

## [更多技术博客](https://vilin.club/)：https://vilin.club/