电网优化系列知识整理（一）——直流潮流计算

直流潮流发的特点是用电力系统的交流潮流（有功功率和无功功率）用等值的直流电流来代替。甚至只用直流电路的解析法来分析电力系统的有功潮流，而根不如你不考虑无功分布对有功的影响。这样一来计算速度加快，但计算的准确度有所降低，本方法适用于对潮流计算准确度要求不高的计算场景。
下面先对直流潮流法的原理进行简单介绍：

上图为直流法的等值图，在上图所示的输电线路中，有功潮流为：

为了快速计算的需要，将上式进行了三项简化：
（1）考虑一般高压电网中线路的电阻远小于电抗，对地电导也可以忽略即 Gii=0 Gij =0
（2）按照标幺值计算时，节点电压与其额定电压相差不大，故有：Ui≈Uj≈1.0；
（3）线路两端的电压相角差（θi-θj）较小，所以有：

这样，上式前两项均为零，只剩第三项

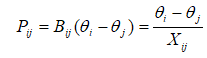
这就相当于线路两端的直流电位分别为θi和θj。线路的直流电阻是Xij。则用矩阵表示为如下式所示。

式中：B0为正常运行时网络的节点电纳矩阵；
θ为网络中各节点的电压相位角的向量；
P为节点注入的有功功率向量；

下面以IEEE39节点系统作为算例来进行直流潮流计算，以说明直流潮流法的具体应用场景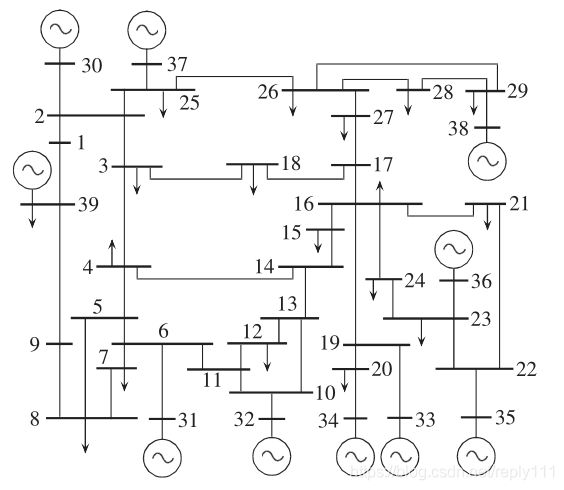
首先通过网络的节点参数得到电纳矩阵B和各个节点的有功注入功率P，然后通过上式得θ=P/B，得到各个节点的电压相角的大小（此出为非精确值，要得到较精确值要进行交流潮流计算），由网络的潮流特性可知，电网中的潮流总是由相连节点中的高相位角的节点流向低相位角的节点，通过直流潮流法的快速计算，可得到网络中各线路的潮流流向，进一步可得到网络的有向邻接矩阵。

function [theta1,P_branch,M,Z,slackbus] = DCpowerflow(mpc)
[n,~] = size(mpc.bus);
[L,~] = size(mpc.branch);
A = zeros(n);%节点导纳矩阵
for i = 1:L
    p = mpc.branch(i,1);q = mpc.branch(i,2);
    A(p,q) = -1/mpc.branch(i,4);
    A(q,p) = A(p,q);
end
for i = 1:n
    A(i,i) = -sum(A(i,:));
end
slackbus = find(mpc.bus(:,2)==3);
A(slackbus,:) = [];
A(:,slackbus) = [];

Z = inv(A);   %%节点阻抗矩阵

P = zeros(n,1);%各个节点的注入功率
[x_gen,~] = size(mpc.gen);
for i = 1:x_gen
    P(mpc.gen(i,1)) = mpc.gen(i,2);
end
P = P - mpc.bus(:,3);
P(slackbus,:) = [];
theta = A\P;

index = (1:n)';index(slackbus) = [];
theta1 = zeros(n,1);%将平衡点的相角加入，形成所有点的相角矢量
[xx,~] = size(index);
for i = 1:xx
    theta1(index(i)) = theta(i);
end
theta1(slackbus) = 0;

P_branch = zeros(L,1);%支路潮流矩阵
for i = 1:L
    p = mpc.branch(i,1);q = mpc.branch(i,2);
    xx = theta1(p) - theta1(q);
    P_branch(i) = xx/mpc.branch(i,4);
end

M = zeros(n,L);%节点支路关联矩阵
for i = 1:L
    p = mpc.branch(i,1);q = mpc.branch(i,2);
    if theta1(p) > theta1(q)
        M(p,i) = 1;M(q,i) = -1;
        if p == slackbus
            M(p,i) = 0;
        elseif q == slackbus
            M(q,i) = 0;        
        end
    else
        M(p,i) = -1;M(q,i) = 1;
        if p == slackbus
            M(p,i) = 0;
        elseif q == slackbus
            M(q,i) = 0; 
        end
    end
end

Github:FancyNum