平衡二叉树（AVL）的实现，附可运行C语言代码

转自：http://www.cnblogs.com/liuliuliu/p/3941748.html

最近几月一直在自学C语言和数据结构，先是写了排序二叉树，觉得平衡二叉树作为一个经典数据结构，有必要实现一下。

网上看了些资料，在AVL和红黑树之间考虑，最后个人还是倾向于AVL。

不同于标准AVL的是，笔者没有使用平衡因子，直接根据左右孩子的高度差值判断是否平衡。整个平衡二叉树是在普通二叉查找树的基础上修改得到的，对于学习数据结构的同学来说，这样逐步提高难度，写起来挑战性没那么大。

代码经测试是可以运行，并实现插入、删除、修改节点时都可以保持平衡。相对于普通二叉查找树，AVL在查找时效率高耗时短，但为了保持高度平衡，必须牺牲插入和删除操作的复杂度。本文将分步讲解如何编写平衡二叉树，全文最后附有完整代码。

当左右子树的高度差超过1时（即≥2，在实际处理时，等于2即为不平衡，进行调整操作，所以不会出现大于2的情况），整棵树失去平衡。写代码之前先了解AVL是如何使二叉树保持平衡，这里涉及到对节点的旋转操作，分四种情况，左左，右右，左右，右左。下面分别解释：

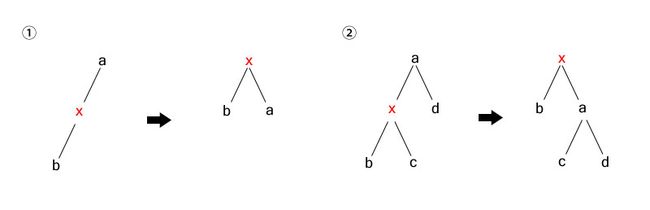
一、左左单旋转

在节点x的左孩子插入节点b

①x无右孩子，旋转节点a即可达到平衡

②x有右孩子c，旋转节点a后，根据a>c>x，需将节点c移动到a的左子树

函数代码如下：

 1 static BTNode *singleRotateLL(BTree *BT, BTNode *phead)
 2 {//不平衡情况为左左的单旋转操作
 3     BTNode *temp;
 4 
 5     if(phead == NULL)
 6         return 0;
 7 
 8     temp = phead->lchild;
 9     
10     if(temp->rchild != NULL){
11         phead->lchild = temp->rchild;
12         phead->lchild->height = tree_node_height(BT, phead->lchild);
13     }
14     else
15         phead->lchild = NULL;
16 
17     temp->rchild = phead;
18     if(temp->rchild->data == BT->phead->data){
19         BT->phead = temp;
20     }
21     phead = temp;
22     temp->rchild->height = tree_node_height(BT, temp->rchild);
23     temp->height = tree_node_height(BT, temp);
24     phead->height = tree_node_height(BT, phead);
25     
26     return phead;
27 }

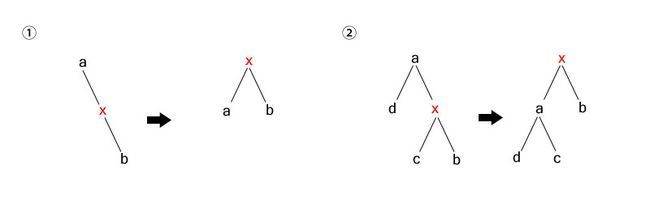
二、右右单旋转

在节点x的右孩子插入节点b

①x无左孩子，旋转节点a即可达到平衡

②x有左孩子c，旋转节点a后，根据x>c>a，需将节点c移动到a的右子树

函数代码如下：

 1 static BTNode *singleRotateRR(BTree *BT, BTNode *phead)
 2 {//不平衡情况为右右的单旋转操作
 3     BTNode *temp;
 4 
 5     if(phead == NULL)
 6         return 0;
 7 
 8     temp = phead->rchild;
 9 
10     if(temp->lchild != NULL){
11         phead->rchild = temp->lchild;
12         phead->rchild->height = tree_node_height(BT, phead->rchild);
13     }
14     else
15         phead->rchild = NULL;
16 
17     temp->lchild = phead;
18     if(temp->lchild->data == BT->phead->data){
19         BT->phead = temp;
20     }
21     phead = temp;
22     temp->lchild->height = tree_node_height(BT, temp->lchild);
23     temp->height = tree_node_height(BT, temp);
24     phead->height = tree_node_height(BT, phead);
25 
26     return phead;
27 }

注：需要注意的是节点旋转后，节点赋值和高度的更新，初学者很容易忽略或是弄错赋值顺序

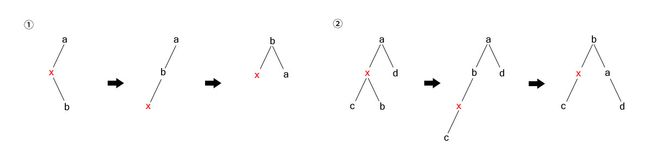
三、左右双旋转

在节点x的右孩子插入节点b

①x无左孩子，②x有左孩子c，这两种情况的处理相同，首先对x节点进行右右单旋转操作，然后对a节点进行左左单旋转操作

函数代码如下：

 1 static BTNode *doubleRotateLR(BTree *BT, BTNode *phead)
 2 {//不平衡情况为左右的双旋转操作
 3     BTNode *temp;
 4 
 5     if(phead == NULL)
 6         return 0;
 7 
 8     temp = phead->lchild;    
 9     phead->lchild = singleRotateRR(BT, temp);
10     temp = phead;
11     phead = singleRotateLL(BT, temp);
12 
13     return phead;
14 }

四、右左双旋转

在节点x的右孩子插入节点b

①x无右孩子，②x有右孩子c，这两种情况的处理相同，首先对x节点进行左左单旋转操作，然后对a节点进行右右单旋转操作

函数代码如下：

 1 static BTNode *doubleRotateRL(BTree *BT, BTNode *phead)
 2 {//不平衡情况为右左的双旋转操作
 3     BTNode *temp;
 4 
 5     if(phead == NULL)
 6         return 0;
 7 
 8     temp = phead->rchild;
 9     phead->rchild = singleRotateLL(BT, temp);
10     temp = phead;
11     phead = singleRotateRR(BT, temp);
12 
13     return phead;
14 }

 

弄清楚了怎样通过旋转达到平衡状态，接下来一步一步构造平衡二叉树。

第一步，我们要在二叉树的节点中加一个属性：高度，在后面的插入和删除函数中将会用到。

结构体代码如下：

1 typedef struct _BTNode{
2     TYPE data;
3     int height;         
4     struct _BTNode *lchild;
5     struct _BTNode *rchild;
6 }BTNode;

 

第二步，需要添加三个辅助函数，一是求节点的高度，而是遍历求树中每个节点的高度（在删除函数中会用到），三是求两个高度的最大值。

 1 static int tree_node_height(BTree *BT, BTNode *phead)
 2 {//求节点的高度，写成函数解决指针为空的情况，默认空节点的高度为-1，只有一个根节点的节点的高度为0，每多一层高度加1
 3     if(phead != NULL){
 4         if(phead->lchild == NULL && phead->rchild == NULL){
 5             return 0;
 6         }
 7         else{
 8             return phead->height = max_height(tree_node_height(BT, phead->lchild), tree_node_height(BT, phead->rchild)) + 1;
 9         }
10     }
11     else{
12         return -1;
13     }
14 }
15 
16 static void tree_height(BTree *BT, BTNode *phead)
17 {//遍历求树中每个节点的高度
18     if(phead == NULL)
19         return;
20 
21     tree_node_height(BT, phead);
22     if(phead->lchild != NULL)
23         tree_node_height(BT, phead->lchild);
24     if(phead->rchild != NULL)
25         tree_node_height(BT, phead->rchild);
26 }
27 
28 static int max_height(int height1, int height2)
29 {//求两个高度的最大值
30     if(height1 > height2)
31         return height1;
32     else
33         return height2;
34 }

 第三步，插入

 插入操作与二叉查找树的操作基本相同，只是在插入后需判断是否平衡，如果不平衡，进行旋转调整。因为BTNode没有使用父节点属性，所以需要用变量存储插入位置，以便调整后可以接回到二叉树上。树顶的根节点需特殊处理

 1 static BOOL tree_add(BTree *BT, BTNode *phead, TYPE value)
 2 {//按序插入结点
 3     if(phead == NULL)
 4         return 0;
 5 
 6     if(phead->data == value)
 7         return 0;
 8 
 9     else{
10         if(phead->data > value){
11             if(phead->lchild == NULL){
12                 BTNode *newnode = (BTNode*)calloc(1, sizeof(BTNode));
13                 newnode->data = value;
14                 newnode->lchild = newnode->rchild = NULL;
15                 phead->lchild = newnode;
16             }
17             else{
18                 tree_add(BT, phead->lchild, value);
19 
20                 //判断插入节点后是否平衡，并调整
21                 BTNode *root;
22                 if(phead = BT->phead)
23                     root = phead;
24                 else
25                     root = phead->lchild;
26             
27                 if(tree_node_height(BT, root->lchild) - tree_node_height(BT, root->rchild) == 2){
28                     if(root->lchild->data > value){
29                         root = singleRotateLL(BT, root);
30                     }
31                     else{
32                         root = doubleRotateLR(BT, root);
33                     }
34                 }
35                 phead = root;
36             }
37         }
38         else{
39             if(phead->rchild == NULL){
40                 BTNode *newnode = (BTNode*)calloc(1, sizeof(BTNode));
41                 newnode->data = value;
42                 newnode->lchild = newnode->rchild = NULL;
43                 phead->rchild = newnode;                    
44             }
45             else{
46                 tree_add(BT, phead->rchild, value);
47                 
48                 //判断插入节点后是否平衡，并调整
49                 BTNode *root;
50                 if(phead = BT->phead)
51                     root = phead;
52                 else
53                     root = phead->rchild;
54                     
55                 if(tree_node_height(BT, root->rchild) - tree_node_height(BT, root->lchild) == 2){
56                     if(root->rchild->data < value){
57                         root = singleRotateRR(BT, root);
58                     }
59                     else{
60                         root = doubleRotateRL(BT, root);
61                     }
62                 }
63                 phead = root;
64             }            
65         }
66             phead->height = tree_node_height(BT, phead);
67             return 1;
68     }
69 
70     return 0;
71 }

第四步，删除

平衡二叉树的删除操作比插入更复杂，因为删除后会引起一系列节点高度的改变，删除后将剩余子树接回二叉树时，要分三种情况处理，被删除节点是：顶部根节点、底部叶子（无子树）、普通节点。

 1 static BOOL tree_del(BTree *BT, BTNode **phead, TYPE value)
 2 {//删除结点
 3     BTNode *temp;
 4     BTNode *root;
 5     int flag;        //flag标记被删除的节点，默认顶部节点flag为0，左边节点flag为-1，右边节点flag为1
 6 
 7     if(*phead == NULL)
 8         return 0;
 9         
10     if(*phead == BT->phead){
11         flag = 0;
12         root = *phead;
13     }
14 
15     else if((*phead)->lchild != NULL){
16         flag = -1;
17         root = (*phead)->lchild;
18     }
19 
20     else if((*phead)->rchild != NULL){
21         flag = 1;
22         root = (*phead)->rchild;
23     }
24     else if((*phead)->lchild == NULL && (*phead)->rchild == NULL)
25         root = *phead;
26     
27     if(root->data == value){
28         if(root->lchild != NULL){
29             temp = BT->search_max(BT, &root->lchild, 1);
30             temp->lchild = root->lchild;
31              temp->rchild = root->rchild;
32             free(root);
33             root = temp;
34             if(flag == 0)
35                 BT->phead = root;
36             else
37                 (*phead)->lchild = root;
38         }
39         else if(root->rchild != NULL){
40             temp = BT->search_min(BT, &root->rchild, 1);   
41             temp->lchild = root->lchild;
42             temp->rchild = root->rchild;
43             free(root);
44             root = temp;
45             if(flag == 0)
46                 BT->phead = root;
47             else
48                 (*phead)->rchild = root;
49         }
50         else{
51             if(flag == 0)
52                 free(*phead);
53             else if(flag = -1){
54                 free((*phead)->lchild);
55                 (*phead)->lchild = NULL;
56             }
57             else if(flag = 1){
58                 free((*phead)->rchild);
59                 (*phead)->rchild = NULL;
60             }
61         }
62          
63         tree_height(BT, BT->phead);    //删除节点后，求每个节点的新高度
64 
65         if(flag == 0)
66             return 1;
67         if(flag == -1){
68             if(tree_node_height(BT, (*phead)->rchild) - tree_node_height(BT, (*phead)->lchild) == 2){
69                 if((*phead)->rchild->rchild != NULL){
70                     root = singleRotateRR(BT, *phead);
71                 }
72                 else{
73                     root = doubleRotateRL(BT, *phead);
74                 }
75             }
76         }
77         else{
78             if(tree_node_height(BT, (*phead)->lchild) - tree_node_height(BT, (*phead)->rchild) == 2){
79                 if((*phead)->lchild->lchild != NULL){
80                     root = singleRotateLL(BT, *phead);
81                 }
82                 else{
83                     root = doubleRotateLR(BT, *phead);
84                 }
85             }
86         }
87             
88         return 1;
89     }
90     else if(root->data > value)
91         return BT->del(BT, &root->lchild, value);
92     else
93         return BT->del(BT, &root->rchild, value);
94 
95     return 0;
96 }

 

除了插入和删除操作，其他操作均与普通二叉查找树一样。

如果读者发现错误或有更好的处理方法，请指出，以便修改完善。