AtCoder Regular Contest 059 题解
https://atcoder.jp/contests/arc059/tasks/arc059
C - いっしょ / Be Together
Time Limit: 2 sec / Memory Limit: 256 MB
Score : 200200 points
Problem Statement
Evi has NN integers a1,a2,..,aNa1,a2,..,aN. His objective is to have NN equal integers by transforming some of them.
He may transform each integer at most once. Transforming an integer xx into another integer yy costs him (x−y)2(x−y)2 dollars. Even if ai=aj(i≠j)ai=aj(i≠j), he has to pay the cost separately for transforming each of them (See Sample 2).
Find the minimum total cost to achieve his objective.
Constraints
- 1≦N≦1001≦N≦100
- −100≦ai≦100−100≦ai≦100
Input
The input is given from Standard Input in the following format:
NN
a1a1 a2a2 ... aNaN
Output
Print the minimum total cost to achieve Evi's objective.
Sample Input 1 Copy
Copy
2
4 8
Sample Output 1 Copy
Copy
8
Transforming the both into 66s will cost (4−6)2+(8−6)2=8(4−6)2+(8−6)2=8 dollars, which is the minimum.
Sample Input 2 Copy
Copy
3
1 1 3
Sample Output 2 Copy
Copy
3
Transforming the all into 22s will cost (1−2)2+(1−2)2+(3−2)2=3(1−2)2+(1−2)2+(3−2)2=3 dollars. Note that Evi has to pay (1−2)2(1−2)2 dollar separately for transforming each of the two 11s.
Sample Input 3 Copy
Copy
3
4 2 5
Sample Output 3 Copy
Copy
5
Leaving the 44 as it is and transforming the 22 and the 55 into 44s will achieve the total cost of (2−4)2+(5−4)2=5(2−4)2+(5−4)2=5 dollars, which is the minimum.
Sample Input 4 Copy
Copy
4
-100 -100 -100 -100
Sample Output 4 Copy
Copy
0
Without transforming anything, Evi's objective is already achieved. Thus, the necessary cost is 00.
水题暴力
#include
using namespace std;
typedef long long ll;
int a[105];
int main() {
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
ll ans=1e18;
ll res=0;
for(int i=-100;i<=100;i++)
{
res=0;
for(int j=1;j<=n;j++)
{
res+=(a[j]-i)*(a[j]-i);
}
ans=min(ans,res);
}
printf("%lld",ans);
return 0;
} D - アンバランス / Unbalanced
Time Limit: 2 sec / Memory Limit: 256 MB
Score : 400400 points
Problem Statement
Given a string tt, we will call it unbalanced if and only if the length of tt is at least 22, and more than half of the letters in tt are the same. For example, both voodoo and melee are unbalanced, while neither noon nor a is.
You are given a string ss consisting of lowercase letters. Determine if there exists a (contiguous) substring of ss that is unbalanced. If the answer is positive, show a position where such a substring occurs in ss.
Constraints
- 2≦|s|≦1052≦|s|≦105
- ss consists of lowercase letters.
Partial Score
- 200200 points will be awarded for passing the test set satisfying 2≦N≦1002≦N≦100.
Input
The input is given from Standard Input in the following format:
ss
Output
If there exists no unbalanced substring of ss, print -1 -1.
If there exists an unbalanced substring of ss, let one such substring be sasa+1...sbsasa+1...sb (1≦a
Sample Input 1 Copy
Copy
needed
Sample Output 1 Copy
Copy
2 5
The string s2s3s4s5s2s3s4s5 == eede is unbalanced. There are also other unbalanced substrings. For example, the output 2 6 will also be accepted.
Sample Input 2 Copy
Copy
atcoder
Sample Output 2 Copy
Copy
-1 -1
The string atcoder contains no unbalanced substring.
分析：
正确子串一定为：XX或者XYX
其他输出-1
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Scanner;
import java.util.TreeMap;
public class Main {
static int mod=1000000007;
public static void main(String[] args) {
Scanner in=new Scanner( new BufferedReader(new InputStreamReader(System.in))) ;
String string=in.next();
int n=string.length();
TreeMap map=new TreeMap();
int l=0,r=0;
long num=0;
for(int i=0;i E - キャンディーとN人の子供 / Children and Candies
Time limit : 4sec / Memory limit : 256MB
Score : 800 points
Problem Statement
12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed. We are very sorry for your inconvenience.
There are N children in AtCoder Kindergarten, conveniently numbered 1 through N. Mr. Evi will distribute C indistinguishable candies to the children.
If child i is given a candies, the child's happiness will become xia, where xi is the child's excitement level. The activity level of the kindergarten is the product of the happiness of all the N children.
For each possible way to distribute C candies to the children by giving zero or more candies to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all possible way to distribute C candies. This sum can be seen as a function of the children's excitement levels x1,..,xN, thus we call it f(x1,..,xN).
You are given integers Ai,Bi(1≦i≦N). Find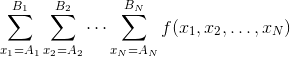 
modulo 109+7.
Constraints
- 1≦N≦400
- 1≦C≦400
- 1≦Ai≦Bi≦400(1≦i≦N)
Partial Score
- 400 points will be awarded for passing the test set satisfying Ai=Bi(1≦i≦N).
Input
The input is given from Standard Input in the following format:
N C A1 A2 ... AN B1 B2 ... BN
Output
Print the value of 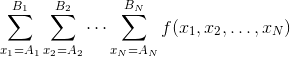modulo 109+7.
Sample Input 1
Copy
2 3 1 1 1 1
Sample Output 1
Copy
4
This case is included in the test set for the partial score, since Ai=Bi. We only have to consider the sum of the activity level of the kindergarten where the excitement level of both child 1 and child 2 are 1 (f(1,1)).
- If child 1 is given 0 candy, and child 2 is given 3 candies, the activity level of the kindergarten is 10*13=1.
- If child 1 is given 1 candy, and child 2 is given 2 candies, the activity level of the kindergarten is 11*12=1.
- If child 1 is given 2 candies, and child 2 is given 1 candy, the activity level of the kindergarten is 12*11=1.
- If child 1 is given 3 candies, and child 2 is given 0 candy, the activity level of the kindergarten is 13*10=1.
Thus, f(1,1)=1+1+1+1=4, and the sum over all f is also 4.
Sample Input 2
Copy
1 2 1 3
Sample Output 2
Copy
14
Since there is only one child, child 1's happiness itself will be the activity level of the kindergarten. Since the only possible way to distribute 2 candies is to give both candies to child 1, the activity level in this case will become the value of f.
- When the excitement level of child 1 is 1, f(1)=12=1.
- When the excitement level of child 1 is 2, f(2)=22=4.
- When the excitement level of child 1 is 3, f(3)=32=9.
Thus, the answer is 1+4+9=14.
Sample Input 3
Copy
2 3 1 1 2 2
Sample Output 3
Copy
66
Since it can be seen that f(1,1)=4,f(1,2)=15,f(2,1)=15,f(2,2)=32, the answer is 4+15+15+32=66.
Sample Input 4
Copy
4 8 3 1 4 1 3 1 4 1
Sample Output 4
Copy
421749
This case is included in the test set for the partial score.
Sample Input 5
Copy
3 100 7 6 5 9 9 9
Sample Output 5
Copy
139123417
题意：n个人，m个糖果，每一个人都有一个x[i](a[i]<=x[i]<=b[i]),计算任何分配方案下,f(x1,x2,...x[n])=,num[i]表示第i个人分的糖果数量,www：全排列。分析：
我们首先设dp[i][j]为前i个人分j个糖果的所有方案累加和，
下一个状态考虑：第i个人分到k个糖果 ，则前面i-1人分j-k个苹果的每个小方案都要乘上(a[i]^k+...+b[i]^k)
即状态转移方程：dp[i][j]+=dp[i-1][j-k]*(a[i]^k+.....b[i]^k) (0<=k<=j)
注意一下mod，如果想加快一下求一下前缀和就行。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Scanner;
import java.util.TreeMap;
public class Main {
static int MOD=1000000007;
static long p[][]=new long[405][405];
static long sum[][]=new long[405][405];
static long dp[][]=new long[405][405];
static long a[]=new long[405];
static long b[]=new long[405];
public static void main(String[] args) {
Scanner in=new Scanner( new BufferedReader(new InputStreamReader(System.in))) ;
for(int i=1;i<=404;i++)//p[i][j]=i^j
{
p[i]= new long[405];
p[i][0]=1;
for(int j=1;j<=404;j++)
{
p[i][j]=(p[i][j-1]*i)%MOD;
}
}
for(int i=1;i<=404;i++)//sum[i][j] 1^j+...+i^j
{
sum[i]=new long[405];
for(int j=0;j<=404;j++)
{
sum[0][j]=0;
sum[i][j]=(sum[i-1][j]%MOD+p[i][j]%MOD)%MOD;
}
}
int n=in.nextInt();
int m=in.nextInt();
for(int i=1;i<=n;i++)
{
a[i]=in.nextLong();
}
for(int i=1;i<=n;i++)
{
b[i]=in.nextLong();
}
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<=j;k++)
{
long temp=(sum[(int) b[i]][k]%MOD-sum[(int) (a[i]-1)][k]%MOD+MOD)%MOD;
dp[i][j]=(dp[i][j]%MOD+dp[i-1][j-k]*temp%MOD)%MOD;
}
}
}
System.out.println(dp[n][m]);
return;
}
}