人智导(十三):有指导学习(Ⅲ)
人智导(十三):有指导学习(Ⅲ)
支持向量机方法
支持向量机方法(Support Vector Machine)
- 寻找一个超平面(决策边界decision boundary)分离数据,以达到分类的目的和效果
- 一种可能的结果
- 另一种可能的结果
- 其它可能的结果
- B 1 B_1 B1和 B 2 B_2 B2,哪一个更好?
- 如何判定哪个更好?
- 寻找具有最大化的空间间隔的超平面(hyperplane) ⇒ \Rightarrow ⇒ B 1 B_1 B1好于 B 2 B_2 B2
- 最大边缘超平面(Maximum Marginal Hyperplane)
计算方法
- 最大化边缘间隔margin: 2 ∥ w ⃗ ∥ \frac{2}{\Vert\vec{w}\Vert} ∥w∥2
- 等同于最小化: L ( w ) = ∥ w ⃗ ∥ 2 2 L(w) = \frac{\Vert \vec{w}\Vert ^2}{2} L(w)=2∥w∥2
- 并且满足如下约束条件: y i = { 1 i f w ⃗ ∙ x ⃗ i + b ≥ 1 − 1 i f w ⃗ ∙ x ⃗ i + b ≤ − 1 e . g . y i ( w ⃗ ∙ x ⃗ i + b ) ≥ 1 y_i = \begin{cases} 1&if~\vec{w}\bullet\vec{x}_i+b\ge 1 \\-1 &if~\vec{w}\bullet \vec{x}_i+b \le -1 \end{cases} e.g.~y_i(\vec{w}\bullet\vec{x}_i +b)\ge 1 yi={1−1if w∙xi+b≥1if w∙xi+b≤−1e.g. yi(w∙xi+b)≥1
- 在数学意义上,约束优化问题(constrained optimization problem)
- 拉格朗日乘子(Lagrange Multiplier) L ( w , b , α ) = 1 2 ∥ w ∥ 2 − Σ i = 1 N α i ( y i ( w ∙ x i + b ) − 1 ) L(w, b, \alpha)=\frac{1}{2}\Vert w\Vert^2-\Sigma^N_{i=1}\alpha_i(y_i(w\bullet x_i +b)-1) L(w,b,α)=21∥w∥2−Σi=1Nαi(yi(w∙xi+b)−1) m i n w , b m a x α i ≥ 0 L ( w , b , α ) = p min_{w, b}max_{\alpha_i \ge 0}L(w, b, \alpha)=p minw,bmaxαi≥0L(w,b,α)=p 有 w = Σ i = 1 N α i y i x i Σ i = 1 N α i y i = 0 w=\Sigma^N_{i=1}\alpha_iy_ix_i~\Sigma^N_{i=1}\alpha_iy_i=0 w=Σi=1Nαiyixi Σi=1Nαiyi=0 分类公式: f ( x ) = s i g n ( w ∙ x + b ) = s i g n ( Σ i = 1 N α i y i x i ∙ x + b ) f(x)=sign(w\bullet x+b)=sign(\Sigma^N_{i=1}\alpha_iy_ix_i\bullet x+b) f(x)=sign(w∙x+b)=sign(Σi=1Nαiyixi∙x+b)
非线性的支持向量机
示例:
- 变换: Φ : ( x 1 , x 2 ) → ( x 1 2 , x 2 2 , 2 x 1 , 2 x 2 , 2 x 1 x 2 , 1 ) \Phi :(x_1, x_2)\to (x^2_1, x^2_2, \sqrt{2}x_1, \sqrt{2}x_2, \sqrt{2}x_1x_2, 1) Φ:(x1,x2)→(x12,x22,2x1,2x2,2x1x2,1)
- 决策边界: w ∙ Φ ( x ) + b = 0 w\bullet \Phi(x)+b = 0 w∙Φ(x)+b=0 w 1 x 1 2 + w 2 x 2 2 + w 3 2 x 1 + w 4 2 x 2 + w 5 2 x 1 x 2 + w 6 + b = 0 w_1x^2_1+w_2x^2_2+w_3\sqrt{2}x_1+w_4\sqrt{2}x_2+w_5\sqrt{2}x_1x_2+w_6+b=0 w1x12+w2x22+w32x1+w42x2+w52x1x2+w6+b=0 f ( x ) = s i g n ( w ∙ Φ ( x ) + b ) = s i g n ( Σ i = 1 N α i y i Φ ( x i ) ∙ Φ ( x ) + b ) f(x)=sign(w\bullet \Phi (x)+b)=sign(\Sigma^N_{i=1}\alpha_iy_i\Phi(x_i)\bullet \Phi (x)+b) f(x)=sign(w∙Φ(x)+b)=sign(Σi=1NαiyiΦ(xi)∙Φ(x)+b)
- 核函数(kernel function): K ( u , v ) = Φ ( u ) ∙ Φ ( v ) = ( u ∙ v + 1 ) 2 K(u, v)=\Phi (u)\bullet \Phi (v)=(u\bullet v+1)^2 K(u,v)=Φ(u)∙Φ(v)=(u∙v+1)2
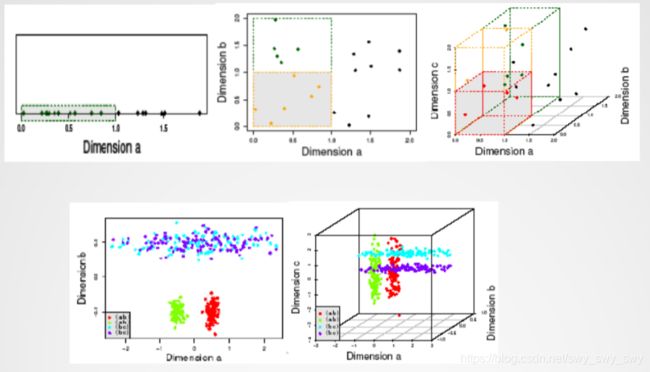
处理高维数据的有效性
- SVM解决分类问题:取决于支持向量的个数,而非数据的样例个数
- 支持向量是关键的训练样例,即最接近决策边界的样例
- 只保留支持向量,同样分离效果的超平面依然可以获得
- SVM方法:只有少量的训练样例——支持向量(support vectors)就能达到好的泛化效果,即使是在数据是高维的情况下。
神经网络方法
神经元(Perceptron 感知器)
Y输出是1,如果三个输入 X 1 , X 2 , X 3 X_1, X_2, X_3 X1,X2,X3中至少有两个是1
| X 1 X_1 X1 | X 2 X_2 X2 | X 3 X_3 X3 | Y Y Y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 |
Y = I ( 0.3 X 1 + 0.3 X 2 + 0.3 X 3 − 0.4 ) w h e r e I ( z ) = { 1 i f z > 0 0 o t h e r w i s e Y=I(0.3X_1+0.3X_2+0.3X_3-0.4) \\ where~I(z)=\begin{cases}1 &if~z>0\\0 &otherwise\end{cases} Y=I(0.3X1+0.3X2+0.3X3−0.4)where I(z)={10if z>0otherwise
线性感知器模型: Y = I ( Σ w i X i − t ) Y=I(\Sigma w_iX_i-t) Y=I(ΣwiXi−t)
n元输入向量 X X X通过点积方式映射到变量 Y Y Y:函数的一种线性表示
n维向量: X X X, W W W
输入: { ( x 1 , y 1 ) , … } \{(x_1, y_1), \dots\} {(x1,y1),…}
输出:线性分类函数 f ( x ) f(x) f(x) f ( x i ) > 0 f o r y i = + 1 f(x_i)>0~for~y_i=+1 f(xi)>0 for yi=+1 f ( x i ) < 0 f o r y i = − 1 f(x_i)<0~for~y_i=-1 f(xi)<0 for yi=−1
f ( x ) ⇒ W X + b = 0 o r w 1 x 1 + w 2 x 2 + b = 0 f(x)\Rightarrow WX + b=0~or~w_1x_1+w_2x_2+b=0 f(x)⇒WX+b=0 or w1x1+w2x2+b=0
Y = s i g n ( Σ i w i X i + b ) Y=sign(\Sigma_iw_iX_i+b) Y=sign(ΣiwiXi+b)
感知器学习算法
Given training examples D
Initialize the weight vector with random values w
repeat
for each training example (x, y) in D
compute the predicted output (1)
for each weight wj do
update the weight (2)
end for
end for
until stop condition is met
其中 D = { ( x i , y i ) ∣ i = 1 , 2 , … , N } D=\{(x_i,y_i)|i=1, 2, \dots ,N\} D={(xi,yi)∣i=1,2,…,N}
( 1 ) : y ^ i ( k ) (1):~\hat{y}^{(k)}_i (1): y^i(k)
( 2 ) : w j ( k + 1 ) = w j ( k ) + λ ( y i − y ^ i ( k ) ) x i j (2):~w^{(k+1)}_j=w^{(k)}_j +\lambda (y_i-\hat{y}^{(k)}_i)x_{ij} (2): wj(k+1)=wj(k)+λ(yi−y^i(k))xij
学习率: 0 < λ < 1 0<\lambda < 1 0<λ<1
神经网络(ANN):实例
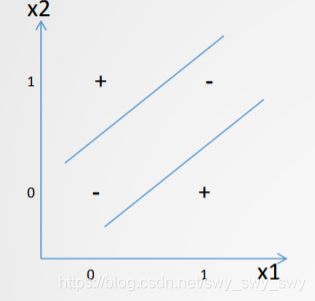
- 异或函数(XOR function)的表示
| x 1 x_1 x1 | x 2 x_2 x2 | y y y |
|---|---|---|
| 0 | 0 | -1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | -1 |
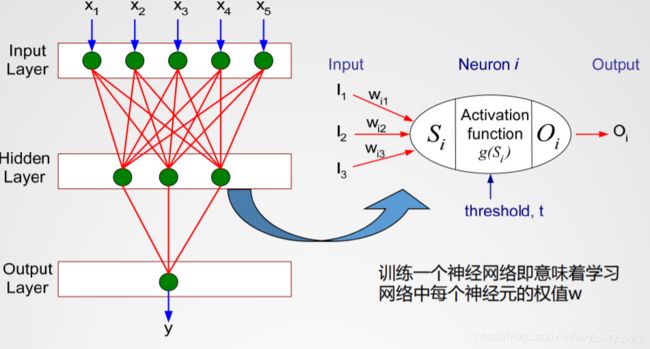
神经网络的一般结构
此为多层前馈式神经网络
每一个节点即为一个神经元
训练一个神经网络即意味着学习网络中每个神经元的权值 w w w
非线性的激活函数
- 神经元的激活函数可以是非线性的,例如最常用的Sigmoid函数(Logistic函数) f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1 z = w ⃗ ∙ x ⃗ + b z=\vec{w}\bullet \vec{x}+b z=w∙x+b
- 函数特点:平滑,取值在0和1区间内 f ( − z ) + f ( z ) = 1 f(-z)+f(z)=1 f(−z)+f(z)=1
- 分类 P ( y = 1 ∣ z ) = f ( z ) P(y=1|z) = f(z) P(y=1∣z)=f(z) P ( y = 0 ∣ z ) = 1 − f ( z ) P(y=0|z)=1-f(z) P(y=0∣z)=1−f(z)
多层(深度)学习神经网络的工作过程
- 训练集中每个样例的特征属性向量作为神经网络的输入
- 输入的向量值被同时供给输入层(input layer)
- 然后通过权值加权计算,结果前馈到隐藏层(hidden layer)
- 最后一个隐藏层加权计算后的输出作为输入层(output layer)的输入部分,展现网络预测结果
- 统计学角度,神经网络实现的是非线性回归。即可解释为:如果网络有足够多的隐藏层节点和训练样例,这个网络就能无限近似于任何一个函数
前馈传播过程(Feed Forward Propagation)
x ⃗ = ( x 1 , x 2 , … , x n ) \vec{x}=(x_1, x_2, \dots ,x_n) x=(x1,x2,…,xn)
O 1 ( h ) = 1 1 + e w ⃗ 0 ∙ x ⃗ + b O^{(h)}_1=\frac{1}{1+e^{\vec{w}_0\bullet \vec{x} +b}} O1(h)=1+ew0∙x+b1
O j ( h ) = 1 1 + e w ⃗ j − 1 ∙ o ⃗ j − 1 + b O^{(h)}_j = \frac{1}{1+e^{\vec{w}_{j-1}\bullet\vec{o}_{j-1}+b}} Oj(h)=1+ewj−1∙oj−1+b1
我们可以把网络看作是输入的传递:给出了输入向量值,就可得出输出向量值
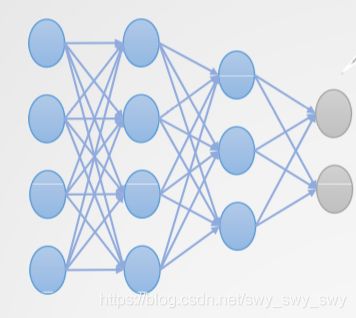
- 隐藏层的个数是随意的,尽管通常应用中只有一个隐藏层
- 含有多个隐藏层,即称之为深度神经网络(deep neural network)
训练神经网络
- 初始化权值 ( w 0 , w 1 , … , w k ) (w_0,w_1,\dots ,w_k) (w0,w1,…,wk):随机取值
- 调整权值,以至于神经网络输出值与给出的那组训练示例类标记一致
- 其目标函数: E ( w ) = Σ i [ Y i − f ( w i , X i ) ] 2 E(w)=\Sigma_i[Y_i-f(w_i,X_i)]^2 E(w)=Σi[Yi−f(wi,Xi)]2
- 即发现合适的权值 w i w_i wi最小化上面的目标函数
- 采用反向传播算法
反向传播(Back Propagation)
计算误差: δ ( 4 ) \delta^{(4)} δ(4)
w j ← w j − λ ∂ E ( w ) ∂ w j w_j\leftarrow w_j-\lambda\frac{\partial E(w)}{\partial w_j} wj←wj−λ∂wj∂E(w)
δ j ( o ) = O j ( 1 − O j ) ( T j − O j ) \delta^{(o)}_j=O_j(1-O_j)(T_j-O_j) δj(o)=Oj(1−Oj)(Tj−Oj)
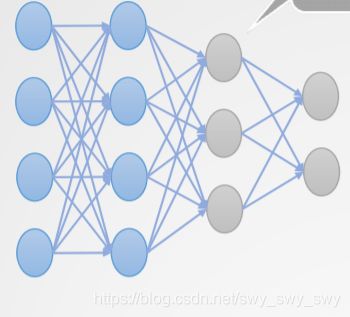
计算误差: δ ( 3 ) \delta^{(3)} δ(3)
w j ← w j − λ ∂ E ( w ) ∂ w j w_j \leftarrow w_j-\lambda\frac{\partial E(w)}{\partial w_j} wj←wj−λ∂wj∂E(w)
δ j ( h ) = O j ( 1 − O j ) Σ k δ k w j k \delta^{(h)}_j = O_j(1-O_j)\Sigma_k\delta_kw_{jk} δj(h)=Oj(1−Oj)Σkδkwjk
w i j = w i j + λ δ j O i w_{ij}=w_{ij}+\lambda\delta_jO_i wij=wij+λδjOi
b j = b j + λ δ j b_j=b_j+\lambda\delta_j bj=bj+λδj
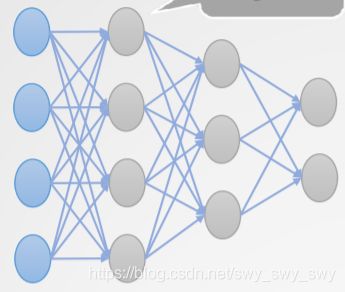
计算误差: δ ( 2 ) \delta^{(2)} δ(2)
w j ← w j − λ ∂ E ( w ) ∂ w j w_j\leftarrow w_j-\lambda\frac{\partial E(w)}{\partial w_j} wj←wj−λ∂wj∂E(w)
δ j ( h ) = O j ( 1 − O j ) Σ k δ k w j k \delta^{(h)}_j=O_j(1-O_j)\Sigma_k\delta_kw_{jk} δj(h)=Oj(1−Oj)Σkδkwjk
w i j = w i j + λ δ j O i w_{ij}=w_{ij}+\lambda\delta_jO_i wij=wij+λδjOi
b j = b j + λ δ j b_j=b_j+\lambda\delta_j bj=bj+λδj
深度神经网络方法的特点
- 优势
- 强的鲁棒性,即使训练样例中含有一定量的噪音或错误的数据,训练的网络模型一样能工作的好
- 预测精度高
- 方法适应性强,适用于现实应用中许多种不同类型的数据
- 并行性
- 弱处
- 网络模型训练时间长
- 需要由经验调试决定大量参数,甚至网络的拓扑结构
- 学习过程中得到的权值及网络中隐藏层单元节点的作用缺少解释意义