java递归绘制谢尔宾斯基三角形
谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基在1915年提出。
构造方法:
1.取一个实心的三角形。(多数使用等边三角形)
2.沿三边中点的连线,将它分成四个小三角形。
3.去掉中间的那一个小三角形。
4.对其余三个小三角形重复1。
以上摘自百度百科:谢尔宾斯基三角形。
实现思路:
创建一个界面类用于绘制,一个递归算法类,一个监听器类。
具体代码如下:
import javax.swing.*;
import java.awt.Graphics;
import java.awt.Dimension;
import java.awt.FlowLayout;
public class SierpinskiT {
//创建窗体对象
JFrame striFrame = new JFrame();
//创建显示窗体的方法
public void showF() {
//创建按钮并添加到窗体上
JButton start = new JButton("开始绘制");
striFrame.add(start);
//设置窗体大小
striFrame.setSize(800, 800);
//设置按钮大小
Dimension size = new Dimension(100,50);
start.setPreferredSize(size);
//设置窗体为流式布局
FlowLayout flow = new FlowLayout();
striFrame.setLayout(flow);
striFrame.setTitle("递归绘制谢尔宾斯基三角形");
//设置窗体可见
striFrame.setVisible(true);
//让窗体获得画笔
Graphics g = striFrame.getGraphics();
//为按钮添加动作监听器
STListener stl = new STListener(g);
start.addActionListener(stl);
}
}
import java.awt.event.*;
import java.awt.Graphics;
public class STListener implements ActionListener{
//声明画笔
private Graphics g;
//重写构造函数将画笔对象传递到监听器类中
public STListener(Graphics g) {
this.g = g;
}
//重写动作监听器方法
public void actionPerformed(ActionEvent e) {
// 创建算法类对象
STalgorithm STtest = new STalgorithm();
//初始坐标,初始三角形边长
int x0 = 400,y0 = 200,d1 = 400;
//调用递归算法绘制
STtest.DrawTri(6, x0, y0, g, d1);
}
}
import java.awt.Graphics;
public class STalgorithm extends javax.swing.JFrame{
//递归算法方法体,以递归层数,三角形顶点坐标,画笔,三角形边长为参数
public void DrawTri(int n,int x0,int y0,Graphics g,int d1) {
//递归出口为递归层数
if(n == 0)
return ;
//根据初始顶点和边长关系计算出另外两个顶点坐标
double x1 = x0-d1/2;
double args = Math.sqrt(3.0)/2;
System.out.println(args);
double y1 = y0+args*d1;
double x2 = x0+d1/2;
double y2 = y0+args*d1;
System.out.println(x0+" "+y0+" "+x1+" "+y1+" "+x2+" "+y2);
//因绘制线段的方法需要整型作为参数故进行强制类型转换
int x1f = (int)x1;
int y1f = (int)y1;
int x2f = (int)x2;
int y2f = (int)y2;
//绘制主三角形
g.drawLine(x0, y0, x2f, y2f);
g.drawLine(x0, y0, x1f, y1f);
g.drawLine(x1f,y1f,x2f,y2f);
//三段线段的中点坐标
int n1x = (x0+x1f)/2;
int n1y = (y1f+y0)/2;
int n2x = (x2f+x0)/2;
int n2y = (y2f+y0)/2;
int n3x = (x2f+x1f)/2;
int n3y = y2f;
//绘制下次递归挖去的三角形
g.drawLine(n1x, n1y, n2x, n2y);
g.drawLine(n2x, n2y, n3x, n3y);
g.drawLine(n1x, n1y, n3x, n3y);
//递归调用绘制方法 递归层数减一 边长减半 以两个中点为新顶点
DrawTri(n-1,n1x,n1y,g,d1/2);
DrawTri(n-1,n2x,n2y,g,d1/2);
DrawTri(n-1,x0,y0,g,d1/2);
}
}
最终效果如图:
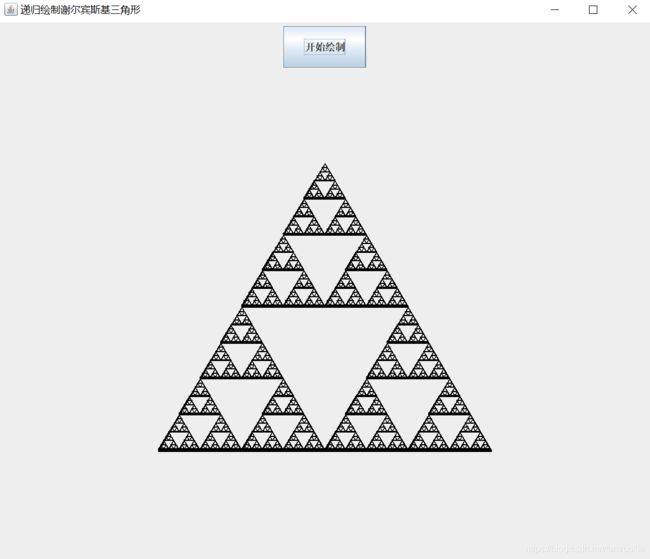
作为一个Java初学者,递归绘制谢尔宾斯基三角形对我来说最大的难点是画笔对象的传递,一开始没有注意画笔对象的传递,出现了空指针报错。
在这个例子中,画笔对象 g 首先在界面类的showF方法中被创建,窗体对象通过getGraphics方法获得了画笔,然后g通过监听器类的构造方法被传递给监听器对象,从而实现了不同类的方法中始终是对同一个画笔对象g进行操作。
递归的代码比起迭代来说简洁了很多,不过在使用的过程中一定要注意递归的终止条件。虽然递归代码简洁,但由于递归工作栈的存在,当递归的层数过多时会出现栈溢出,在实际生活中要根据情况来使用递归。